Tensor field of valence 0 (or component of a tensorial field). More...
#include <scalar.h>
Public Member Functions | |
| Scalar (const Map &mpi) | |
| Constructor from mapping. More... | |
| Scalar (const Tensor &a) | |
| Constructor from a Tensor (must be of valence 0) More... | |
| Scalar (const Scalar &a) | |
| Copy constructor. More... | |
| Scalar (const Cmp &a) | |
| Constructor by conversion of a Cmp. More... | |
| Scalar (const Map &, const Mg3d &, FILE *) | |
Constructor from a file (see sauve(FILE*) ) More... | |
| virtual | ~Scalar () |
| Destructor. More... | |
| virtual void | set_etat_nondef () |
Sets the logical state to ETATNONDEF (undefined). More... | |
| virtual void | set_etat_zero () |
Sets the logical state to ETATZERO (zero). More... | |
| virtual void | set_etat_qcq () |
Sets the logical state to ETATQCQ (ordinary state). More... | |
| void | set_etat_one () |
Sets the logical state to ETATUN (one). More... | |
| virtual void | allocate_all () |
Sets the logical state to ETATQCQ (ordinary state) and performs the memory allocation of all the elements, down to the double arrays of the Tbl s. More... | |
| void | annule_hard () |
Sets the Scalar to zero in a hard way. More... | |
| int | get_etat () const |
Returns the logical state ETATNONDEF (undefined), ETATZERO (null) or ETATQCQ (ordinary). More... | |
| int | get_dzpuis () const |
Returns dzpuis. More... | |
| bool | dz_nonzero () const |
Returns true if the last domain is compactified and *this is not zero in this domain. More... | |
| bool | check_dzpuis (int dzi) const |
Returns false if the last domain is compactified and *this is not zero in this domain and dzpuis is not equal to dzi , otherwise return true. More... | |
| bool | is_nan (bool verbose=false) const |
| Looks for NaNs (not a number) in the scalar field. More... | |
| void | operator= (const Scalar &a) |
Assignment to another Scalar defined on the same mapping. More... | |
| virtual void | operator= (const Tensor &a) |
Assignment to a Tensor (of valence 0) More... | |
| void | operator= (const Cmp &a) |
Assignment to a Cmp. More... | |
| void | operator= (const Valeur &a) |
Assignment to a Valeur. More... | |
| void | operator= (const Mtbl &a) |
Assignment to a Mtbl. More... | |
| void | operator= (double) |
Assignment to a double. More... | |
| void | operator= (int) |
Assignment to an int. More... | |
| operator Cmp () const | |
Conversion to a Cmp. More... | |
| const Valeur & | get_spectral_va () const |
Returns va (read only version) More... | |
| Valeur & | set_spectral_va () |
Returns va (read/write version) More... | |
| Tbl & | set_domain (int l) |
| Read/write of the value in a given domain. More... | |
| const Tbl & | domain (int l) const |
| Read-only of the value in a given domain. More... | |
| double | val_grid_point (int l, int k, int j, int i) const |
| Returns the value of the field at a specified grid point. More... | |
| double | val_point (double r, double theta, double phi) const |
Computes the value of the field at an arbitrary point 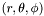 , by means of the spectral expansion. More... , by means of the spectral expansion. More... | |
| double & | set_grid_point (int l, int k, int j, int i) |
| Setting the value of the field at a given grid point. More... | |
| virtual void | annule (int l_min, int l_max) |
Sets the Scalar to zero in several domains. More... | |
| void | set_inner_boundary (int l, double x) |
Sets the value of the Scalar at the inner boundary of a given domain. More... | |
| void | set_outer_boundary (int l, double x) |
Sets the value of the Scalar at the outer boundary of a given domain. More... | |
| Tbl | multipole_spectrum () const |
| Gives the spectrum in terms of multipolar modes l . More... | |
| Tbl | tbl_out_bound (int l_dom, bool leave_ylm=false) |
Returns the Tbl containing the values of angular coefficients at the outer boundary. More... | |
| Tbl | tbl_in_bound (int n, bool leave_ylm=false) |
Returns the Tbl containing the values of angular coefficients at the inner boundary. More... | |
| Scalar | scalar_out_bound (int n, bool leave_ylm=false) |
Returns the Scalar containing the values of angular coefficients at the outer boundary. More... | |
| const Scalar & | dsdr () const |
Returns 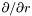 of of *this . More... | |
| const Scalar & | srdsdt () const |
Returns 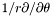 of of *this . More... | |
| const Scalar & | srstdsdp () const |
Returns 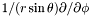 of of *this . More... | |
| const Scalar & | dsdt () const |
Returns 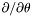 of of *this . More... | |
| const Scalar & | dsdradial () const |
Returns 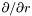 of of *this if the mapping is affine (class Map_af) and 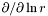 of of *this if the mapping is logarithmic (class Map_log). More... | |
| const Scalar & | dsdrho () const |
Returns 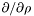 of of *this . More... | |
| const Scalar & | stdsdp () const |
Returns 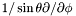 of of *this . More... | |
| const Scalar & | dsdx () const |
Returns 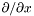 of of *this , where 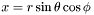 . More... . More... | |
| const Scalar & | dsdy () const |
Returns 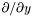 of of *this , where 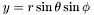 . More... . More... | |
| const Scalar & | dsdz () const |
Returns 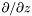 of of *this , where 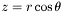 . More... . More... | |
| const Scalar & | deriv (int i) const |
Returns 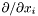 of of *this , where 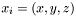 . More... . More... | |
| const Vector & | derive_cov (const Metric &gam) const |
Returns the gradient (1-form = covariant vector) of *this More... | |
| const Vector & | derive_con (const Metric &gam) const |
Returns the "contravariant" derivative of *this with respect to some metric  , by raising the index of the gradient (cf. More... , by raising the index of the gradient (cf. More... | |
| Scalar | derive_lie (const Vector &v) const |
Computes the derivative of this along a vector field v. More... | |
| const Scalar & | laplacian (int ced_mult_r=4) const |
Returns the Laplacian of *this. More... | |
| const Scalar & | lapang () const |
Returns the angular Laplacian 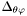 of of *this , where 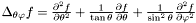 . More... . More... | |
| void | div_r () |
Division by r everywhere; dzpuis is not changed. More... | |
| void | div_r_dzpuis (int ced_mult_r) |
Division by r everywhere but with the output flag dzpuis set to ced_mult_r . More... | |
| void | div_r_ced () |
Division by r in the compactified external domain (CED), the dzpuis flag is not changed. More... | |
| void | mult_r () |
Multiplication by r everywhere; dzpuis is not changed. More... | |
| void | mult_r_dzpuis (int ced_mult_r) |
Multiplication by r everywhere but with the output flag dzpuis set to ced_mult_r . More... | |
| void | mult_r_ced () |
Multiplication by r in the compactified external domain (CED), the dzpuis flag is not changed. More... | |
| void | mult_rsint () |
Multiplication by 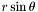 everywhere; everywhere; dzpuis is not changed. More... | |
| void | mult_rsint_dzpuis (int ced_mult_r) |
Multiplication by 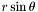 but with the output flag but with the output flag dzpuis set to ced_mult_r . More... | |
| void | div_rsint () |
Division by 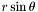 everywhere; everywhere; dzpuis is not changed. More... | |
| void | div_rsint_dzpuis (int ced_mult_r) |
Division by 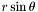 but with the output flag but with the output flag dzpuis set to ced_mult_r . More... | |
| void | mult_cost () |
Multiplication by 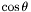 . More... . More... | |
| void | div_cost () |
Division by 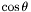 . More... . More... | |
| void | mult_sint () |
Multiplication by 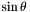 . More... . More... | |
| void | div_sint () |
Division by 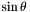 . More... . More... | |
| void | div_tant () |
Division by 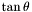 . More... . More... | |
| Scalar | primr (bool null_infty=true) const |
Computes the radial primitive which vanishes for 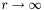 . More... . More... | |
| double | integrale () const |
Computes the integral over all space of *this . More... | |
| const Tbl & | integrale_domains () const |
Computes the integral in each domain of *this . More... | |
| virtual void | dec_dzpuis (int dec=1) |
Decreases by dec units the value of dzpuis and changes accordingly the values of the Scalar in the compactified external domain (CED). More... | |
| virtual void | inc_dzpuis (int inc=1) |
Increases by inc units the value of dzpuis and changes accordingly the values of the Scalar in the compactified external domain (CED). More... | |
| virtual void | change_triad (const Base_vect &new_triad) |
| Sets a new vectorial basis (triad) of decomposition and modifies the components accordingly. More... | |
| void | filtre (int n) |
Sets the n lasts coefficients in r to 0 in the external domain. More... | |
| void | filtre_r (int *nn) |
Sets the n lasts coefficients in r to 0 in all domains. More... | |
| void | filtre_r (int n, int nzone) |
Sets the n last coefficients in r to 0 in the domain nzone . More... | |
| virtual void | exponential_filter_r (int lzmin, int lzmax, int p, double alpha=-16.) |
| Applies an exponential filter to the spectral coefficients in the radial direction. More... | |
| void | sarra_filter_r (int lzmin, int lzmax, double p, double alpha=-1E-16) |
| Applies an exponential filter to the spectral coefficients in the radial direction. More... | |
| void | exp_filter_r_all_domains (Scalar &ss, int p, double alpha=-16.) |
| Applies an exponential filter in radial direction in all domains. More... | |
| void | sarra_filter_r_all_domains (double p, double alpha=1E-16) |
Applies an exponential filter in radial direction in all domains for the case where p is a double (see Scalar:sarra_filter_r ). More... | |
| virtual void | exponential_filter_ylm (int lzmin, int lzmax, int p, double alpha=-16.) |
| Applies an exponential filter to the spectral coefficients in the angular directions. More... | |
| virtual void | exponential_filter_ylm_phi (int lzmin, int lzmax, int p_r, int p_tet, int p_phi, double alpha=-16.) |
| Applies an exponential filter to the spectral coefficients in the angular directions. More... | |
| void | annule_l (int l_min, int l_max, bool ylm_output=false) |
Sets all the multipolar components between l_min and l_max to zero. More... | |
| void | filtre_phi (int n, int zone) |
Sets the n lasts coefficients in 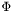 to 0 in the domain to 0 in the domain zone . More... | |
| void | filtre_tp (int nn, int nz1, int nz2) |
Sets the n lasts coefficients in  to 0 in the domain to 0 in the domain nz1 to nz2 when expressed in spherical harmonics. More... | |
| void | copy_coefs_from_small_grid (const Scalar &scal_small_grid) |
Copies the content of the argument Scalar to this defined on a larger grid, with similar mappings. More... | |
| void | copy_coefs_from_large_grid (const Scalar &scal_large_grid) |
Copies the content of the argument Scalar to this defined on a smaller grid, with similar mappings. More... | |
| void | fixe_decroissance (int puis) |
Substracts all the components behaving like 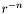 in the external domain, with n strictly lower than in the external domain, with n strictly lower than puis , so that *this decreases at least like 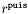 at infinity. More... at infinity. More... | |
| void | smooth_decay (int k, int n) |
Performs a 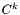 matching of the last non-compactified shell with a decaying function matching of the last non-compactified shell with a decaying function 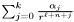 where where 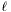 is the spherical harmonic index and n is some specifiable parameter. More... is the spherical harmonic index and n is some specifiable parameter. More... | |
| void | raccord (int n) |
Performs the 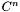 matching of the nucleus with respect to the first shell. More... matching of the nucleus with respect to the first shell. More... | |
| void | raccord_c1_zec (int puis, int nbre, int lmax) |
Performs the 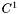 matching of the external domain with respect to the last shell using function like matching of the external domain with respect to the last shell using function like 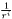 with with 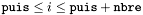 for each spherical harmonics with for each spherical harmonics with 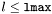 . More... . More... | |
| void | raccord_externe (int puis, int nbre, int lmax) |
| Matching of the external domain with the outermost shell. More... | |
| void | match_tau (Param &par_bc, Param *par_mat=0x0) |
| Method for matching accross domains and imposing boundary condition. More... | |
| void | match_tau_star (Param &par_bc, Param *par_mat=0x0) |
| Method for matching accross domains and imposing boundary condition. More... | |
| void | match_tau_shell (Param &par_bc, Param *par_mat=0x0) |
| Method for matching accross domains and imposing boundary condition. More... | |
| void | match_collocation (Param &par_bc, Param *par_mat=0x0) |
| Method for matching accross domains and imposing boundary condition. More... | |
| virtual void | sauve (FILE *) const |
| Save in a file. More... | |
| virtual void | spectral_display (const char *comment=0x0, double threshold=1.e-7, int precision=4, ostream &ostr=cout) const |
| Displays the spectral coefficients and the associated basis functions. More... | |
| void | visu_section (const char section_type, double aa, double umin, double umax, double vmin, double vmax, const char *title=0x0, const char *filename=0x0, bool start_dx=true, int nu=200, int nv=200) const |
| 3D visualization via a plane section. More... | |
| void | visu_section (const Tbl &plane, double umin, double umax, double vmin, double vmax, const char *title=0x0, const char *filename=0x0, bool start_dx=true, int nu=200, int nv=200) const |
| 3D visualization via a plane section. More... | |
| void | visu_section_anim (const char section_type, double aa, double umin, double umax, double vmin, double vmax, int jtime, double ttime, int jgraph=1, const char *title=0x0, const char *filename_root=0x0, bool start_dx=false, int nu=200, int nv=200) const |
| 3D visualization via time evolving plane section (animation). More... | |
| void | visu_box (double xmin, double xmax, double ymin, double ymax, double zmin, double zmax, const char *title0=0x0, const char *filename0=0x0, bool start_dx=true, int nx=40, int ny=40, int nz=40) const |
| 3D visualization (volume rendering) via OpenDX. More... | |
| void | operator+= (const Scalar &) |
| += Scalar More... | |
| void | operator-= (const Scalar &) |
| -= Scalar More... | |
| void | operator*= (const Scalar &) |
| *= Scalar More... | |
| virtual void | std_spectral_base () |
Sets the spectral bases of the Valeur va to the standard ones for a scalar field. More... | |
| virtual void | std_spectral_base_odd () |
Sets the spectral bases of the Valeur va to the standard odd ones for a scalar field. More... | |
| void | set_spectral_base (const Base_val &) |
Sets the spectral bases of the Valeur va More... | |
| const Base_val & | get_spectral_base () const |
Returns the spectral bases of the Valeur va. More... | |
| void | set_dzpuis (int) |
Modifies the dzpuis flag. More... | |
| Valeur ** | asymptot (int n, const int flag=0) const |
| Asymptotic expansion at r = infinity. More... | |
| Scalar | poisson () const |
Solves the scalar Poisson equation with *this as a source. More... | |
| void | poisson (Param &par, Scalar &uu) const |
Solves the scalar Poisson equation with *this as a source (version with parameters to control the resolution). More... | |
| Scalar | poisson_tau () const |
Solves the scalar Poisson equation with *this as a source using a real Tau method The source  of the equation of the equation 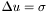 is represented by the is represented by the Scalar *this . More... | |
| void | poisson_tau (Param &par, Scalar &uu) const |
Solves the scalar Poisson equation with *this as a source using a real Tau method (version with parameters to control the resolution) The source  of the equation of the equation 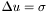 is represented by the is represented by the Scalar *this . More... | |
| Scalar | poisson_dirichlet (const Valeur &limite, int num) const |
Is identicall to Scalar::poisson() . More... | |
| Scalar | poisson_neumann (const Valeur &, int) const |
Idem as Scalar::poisson_dirichlet , the boundary condition being on the radial derivative of the solution. More... | |
| Scalar | poisson_dir_neu (const Valeur &limite, int num, double fact_dir, double fact_neu) const |
Is identicall to Scalar::poisson() . More... | |
| Scalar | poisson_frontiere_double (const Valeur &, const Valeur &, int) const |
Idem as Scalar::poisson_dirichlet , the boundary condition being on both the function and its radial derivative. More... | |
| void | poisson_regular (int k_div, int nzet, double unsgam1, Param &par, Scalar &uu, Scalar &uu_regu, Scalar &uu_div, Tensor &duu_div, Scalar &source_regu, Scalar &source_div) const |
Solves the scalar Poisson equation with *this as a source (version with parameters to control the resolution). More... | |
| Tbl | test_poisson (const Scalar &uu, ostream &ostr, bool detail=false) const |
Checks if a Poisson equation with *this as a source has been correctly solved. More... | |
| Scalar | poisson_angu (double lambda=0) const |
Solves the (generalized) angular Poisson equation with *this as source. More... | |
| Scalar | avance_dalembert (Param &par, const Scalar &fJm1, const Scalar &source) const |
Performs one time-step integration (from 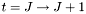 ) of the scalar d'Alembert equation with ) of the scalar d'Alembert equation with *this being the value of the function f at time J . More... | |
| Scalar | sol_elliptic (Param_elliptic ¶ms) const |
| Resolution of a general elliptic equation, putting zero at infinity. More... | |
| Scalar | sol_elliptic_boundary (Param_elliptic ¶ms, const Mtbl_cf &bound, double fact_dir, double fact_neu) const |
| Resolution of a general elliptic equation, putting zero at infinity and with inner boundary conditions. More... | |
| Scalar | sol_elliptic_boundary (Param_elliptic ¶ms, const Scalar &bound, double fact_dir, double fact_neu) const |
| Resolution of general elliptic equation, with inner boundary conditions as Scalars on mono-domain angulare grids. More... | |
| Scalar | sol_elliptic_2d (Param_elliptic &) const |
Solves the scalar 2-dimensional elliptic equation with *this as a source. More... | |
| Scalar | sol_elliptic_pseudo_1d (Param_elliptic &) const |
Solves a pseudo-1d elliptic equation with *this as a source. More... | |
| Scalar | sol_elliptic_no_zec (Param_elliptic ¶ms, double val=0) const |
| Resolution of a general elliptic equation, putting a given value at the outermost shell and not solving in the compactified domain. More... | |
| Scalar | sol_elliptic_only_zec (Param_elliptic ¶ms, double val) const |
| Resolution of a general elliptic equation solving in the compactified domain and putting a given value at the inner boundary. More... | |
| Scalar | sol_elliptic_sin_zec (Param_elliptic ¶ms, double *coefs, double *phases) const |
| General elliptic solver. More... | |
| Scalar | sol_elliptic_fixe_der_zero (double val, Param_elliptic ¶ms) const |
| Resolution of a general elliptic equation fixing the dericative at the origin and relaxing one continuity condition. More... | |
| Scalar | sol_divergence (int n) const |
| Resolution of a divergence-like equation. More... | |
| void | import (const Scalar &ci) |
Assignment to another Scalar defined on a different mapping. More... | |
| void | import_symy (const Scalar &ci) |
Assignment to another Scalar defined on a different mapping. More... | |
| void | import_asymy (const Scalar &ci) |
Assignment to another Scalar defined on a different mapping. More... | |
| void | import (int nzet, const Scalar &ci) |
Assignment to another Scalar defined on a different mapping. More... | |
| void | import_symy (int nzet, const Scalar &ci) |
Assignment to another Scalar defined on a different mapping. More... | |
| void | import_asymy (int nzet, const Scalar &ci) |
Assignment to another Scalar defined on a different mapping. More... | |
| void | set_triad (const Base_vect &new_triad) |
| Assigns a new vectorial basis (triad) of decomposition. More... | |
| Scalar & | set (const Itbl &ind) |
| Returns the value of a component (read/write version). More... | |
| Scalar & | set (int i1, int i2) |
| Returns the value of a component for a tensor of valence 2 (read/write version). More... | |
| Scalar & | set (int i1, int i2, int i3) |
| Returns the value of a component for a tensor of valence 3 (read/write version). More... | |
| Scalar & | set (int i1, int i2, int i3, int i4) |
| Returns the value of a component for a tensor of valence 4 (read/write version). More... | |
| void | annule_domain (int l) |
Sets the Tensor to zero in a given domain. More... | |
| void | annule_extern_cn (int l_0, int deg) |
| Performs a smooth (C^n) transition in a given domain to zero. More... | |
| void | copy_coefs_from_smaller_grid (const Tensor &tens_small_grid) |
Copies the content of the argument Tensor to this defined on a larger grid, with similar mappings. More... | |
| void | copy_coefs_from_larger_grid (const Tensor &tens_large_grid) |
Copies the content of the argument Tensor to this defined on a smaller grid, with similar mappings. More... | |
| const Tensor & | divergence (const Metric &gam) const |
Computes the divergence of this with respect to some metric  . More... . More... | |
| Tensor | up (int ind, const Metric &gam) const |
Computes a new tensor by raising an index of *this. More... | |
| Tensor | down (int ind, const Metric &gam) const |
Computes a new tensor by lowering an index of *this. More... | |
| Tensor | up_down (const Metric &gam) const |
Computes a new tensor by raising or lowering all the indices of *this . More... | |
| Tensor | trace (int ind1, int ind2) const |
| Trace on two different type indices. More... | |
| Tensor | trace (int ind1, int ind2, const Metric &gam) const |
| Trace with respect to a given metric. More... | |
| Scalar | trace () const |
| Trace on two different type indices for a valence 2 tensor. More... | |
| Scalar | trace (const Metric &gam) const |
| Trace with respect to a given metric for a valence 2 tensor. More... | |
| virtual int | position (const Itbl &ind) const |
Returns the position in the array cmp of a component given by its indices. More... | |
| virtual Itbl | indices (int pos) const |
Returns the indices of a component given by its position in the array cmp . More... | |
| const Map & | get_mp () const |
| Returns the mapping. More... | |
| const Base_vect * | get_triad () const |
| Returns the vectorial basis (triad) on which the components are defined. More... | |
| int | get_valence () const |
| Returns the valence. More... | |
| int | get_n_comp () const |
| Returns the number of stored components. More... | |
| int | get_index_type (int i) const |
Gives the type (covariant or contravariant) of the index number i . More... | |
| Itbl | get_index_type () const |
| Returns the types of all the indices. More... | |
| int & | set_index_type (int i) |
Sets the type of the index number i . More... | |
| Itbl & | set_index_type () |
| Sets the types of all the indices. More... | |
| const Scalar & | operator() (const Itbl &ind) const |
| Returns the value of a component (read-only version). More... | |
| const Scalar & | operator() (int i1, int i2) const |
| Returns the value of a component for a tensor of valence 2 (read-only version). More... | |
| const Scalar & | operator() (int i1, int i2, int i3) const |
| Returns the value of a component for a tensor of valence 3 (read-only version). More... | |
| const Scalar & | operator() (int i1, int i2, int i3, int i4) const |
| Returns the value of a component for a tensor of valence 4 (read-only version). More... | |
| void | operator+= (const Tensor &) |
| += Tensor More... | |
| void | operator-= (const Tensor &) |
| -= Tensor More... | |
Protected Member Functions | |
| void | del_t () |
| Logical destructor. More... | |
| virtual void | del_deriv () const |
| Logical destructor of the derivatives. More... | |
| void | set_der_0x0 () const |
| Sets the pointers for derivatives to 0x0. More... | |
| void | import_gal (int nzet, const Scalar &ci) |
Assignment to another Scalar defined on a different mapping, when the two mappings do not have a particular relative orientation. More... | |
| void | import_align (int nzet, const Scalar &ci) |
Assignment to another Scalar defined on a different mapping, when the two mappings have aligned Cartesian axis. More... | |
| void | import_anti (int nzet, const Scalar &ci) |
Assignment to another Scalar defined on a different mapping, when the two mappings have anti-aligned Cartesian axis (i.e. More... | |
| void | import_align_symy (int nzet, const Scalar &ci) |
Assignment to another Scalar defined on a different mapping, when the two mappings have aligned Cartesian axis. More... | |
| void | import_anti_symy (int nzet, const Scalar &ci) |
Assignment to another Scalar defined on a different mapping, when the two mappings have anti-aligned Cartesian axis (i.e. More... | |
| void | import_align_asymy (int nzet, const Scalar &ci) |
Assignment to another Scalar defined on a different mapping, when the two mappings have aligned Cartesian axis. More... | |
| void | import_anti_asymy (int nzet, const Scalar &ci) |
Assignment to another Scalar defined on a different mapping, when the two mappings have anti-aligned Cartesian axis (i.e. More... | |
| virtual void | del_derive_met (int) const |
Logical destructor of the derivatives depending on the i-th element of met_depend . More... | |
| void | set_der_met_0x0 (int) const |
Sets all the i-th components of met_depend , p_derive_cov , etc... More... | |
| void | set_dependance (const Metric &) const |
To be used to describe the fact that the derivatives members have been calculated with met . More... | |
| int | get_place_met (const Metric &) const |
Returns the position of the pointer on metre in the array met_depend . More... | |
| void | compute_derive_lie (const Vector &v, Tensor &resu) const |
Computes the Lie derivative of this with respect to some vector field v (protected method; the public interface is method derive_lie ). More... | |
Protected Attributes | |
| int | etat |
The logical state ETATNONDEF (undefined), ETATZERO (null), ETATUN (one), or ETATQCQ (ordinary). More... | |
| int | dzpuis |
Power of r by which the quantity represented by this must be divided in the compactified external domain (CED) in order to get the correct physical values. More... | |
| Valeur | va |
The numerical value of the Scalar. More... | |
| Scalar * | p_dsdr |
Pointer on 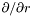 of of *this (0x0 if not up to date) More... | |
| Scalar * | p_srdsdt |
Pointer on 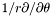 of of *this (0x0 if not up to date) More... | |
| Scalar * | p_srstdsdp |
Pointer on 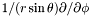 of of *this (0x0 if not up to date) More... | |
| Scalar * | p_dsdt |
Pointer on 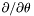 of of *this (0x0 if not up to date) More... | |
| Scalar * | p_stdsdp |
Pointer on 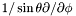 of of *this (0x0 if not up to date) More... | |
| Scalar * | p_dsdx |
Pointer on 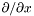 of of *this , where 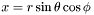 (0x0 if not up to date) More... (0x0 if not up to date) More... | |
| Scalar * | p_dsdy |
Pointer on 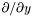 of of *this , where 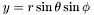 (0x0 if not up to date) More... (0x0 if not up to date) More... | |
| Scalar * | p_dsdz |
Pointer on 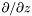 of of *this , where 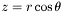 (0x0 if not up to date) More... (0x0 if not up to date) More... | |
| Scalar * | p_lap |
Pointer on the Laplacian of *this (0x0 if not up to date) More... | |
| Scalar * | p_lapang |
Pointer on the Laplacian of *this (0x0 if not up to date) More... | |
| Scalar * | p_dsdradial |
Pointer on 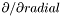 of of *this. More... | |
| Scalar * | p_dsdrho |
Pointer on 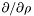 of of *this. More... | |
| int | ind_lap |
| Power of r by which the last computed Laplacian has been multiplied in the compactified external domain. More... | |
| Tbl * | p_integ |
Pointer on the space integral of *this (values in each domain) (0x0 if not up to date) More... | |
| const Map *const | mp |
| Mapping on which the numerical values at the grid points are defined. More... | |
| int | valence |
| Valence of the tensor (0 = scalar, 1 = vector, etc...) More... | |
| const Base_vect * | triad |
| Vectorial basis (triad) with respect to which the tensor components are defined. More... | |
| Itbl | type_indice |
1D array of integers (class Itbl ) of size valence containing the type of each index: COV for a covariant one and CON for a contravariant one. More... | |
| int | n_comp |
| Number of stored components, depending on the symmetry. More... | |
| Scalar ** | cmp |
Array of size n_comp of pointers onto the components. More... | |
| const Metric * | met_depend [N_MET_MAX] |
Array on the Metric 's which were used to compute derived quantities, like p_derive_cov , etc... More... | |
| Tensor * | p_derive_cov [N_MET_MAX] |
Array of pointers on the covariant derivatives of this with respect to various metrics. More... | |
| Tensor * | p_derive_con [N_MET_MAX] |
Array of pointers on the contravariant derivatives of this with respect to various metrics. More... | |
| Tensor * | p_divergence [N_MET_MAX] |
Array of pointers on the divergence of this with respect to various metrics. More... | |
Friends | |
| ostream & | operator<< (ostream &, const Scalar &) |
| Display. More... | |
| Scalar | operator- (const Scalar &) |
- Scalar More... | |
| Scalar | operator+ (const Scalar &, const Scalar &) |
| Scalar + Scalar. More... | |
| Scalar | operator+ (const Scalar &, const Mtbl &) |
| Scalar + Mbtl. More... | |
| Scalar | operator+ (const Scalar &, double) |
| Scalar + double. More... | |
| Scalar | operator- (const Scalar &, const Scalar &) |
| Scalar - Scalar. More... | |
| Scalar | operator- (const Scalar &, const Mtbl &) |
| Scalar - Mbtl. More... | |
| Scalar | operator- (const Scalar &, double) |
| Scalar - double. More... | |
| Scalar | operator* (const Scalar &, const Scalar &) |
| Scalar * Scalar. More... | |
| Scalar | operator% (const Scalar &, const Scalar &) |
| Scalar * Scalar with desaliasing. More... | |
| Scalar | operator| (const Scalar &, const Scalar &) |
| Scalar * Scalar with desaliasing only in r. More... | |
| Scalar | operator* (const Mtbl &, const Scalar &) |
| Mtbl * Scalar. More... | |
| Scalar | operator* (double, const Scalar &) |
| double * Scalar More... | |
| Scalar | operator/ (const Scalar &, const Scalar &) |
| Scalar / Scalar. More... | |
| Scalar | operator/ (const Scalar &, const Mtbl &) |
| Scalar / Mtbl. More... | |
| Scalar | operator/ (const Mtbl &, const Scalar &) |
| Mtbl / Scalar. More... | |
| Scalar | operator/ (const Scalar &, double) |
| Scalar / double. More... | |
| Scalar | operator/ (double, const Scalar &) |
| double / Scalar More... | |
| Scalar | sin (const Scalar &) |
| Sine. More... | |
| Scalar | cos (const Scalar &) |
| Cosine. More... | |
| Scalar | tan (const Scalar &) |
| Tangent. More... | |
| Scalar | asin (const Scalar &) |
| Arcsine. More... | |
| Scalar | acos (const Scalar &) |
| Arccosine. More... | |
| Scalar | atan (const Scalar &) |
| Arctangent. More... | |
| Scalar | exp (const Scalar &) |
| Exponential. More... | |
| Scalar | Heaviside (const Scalar &) |
| Heaviside function. More... | |
| Scalar | log (const Scalar &) |
| Neperian logarithm. More... | |
| Scalar | log10 (const Scalar &) |
| Basis 10 logarithm. More... | |
| Scalar | sqrt (const Scalar &) |
| Square root. More... | |
| Scalar | racine_cubique (const Scalar &) |
| Cube root. More... | |
| Scalar | pow (const Scalar &, int) |
Power 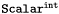 . More... . More... | |
| Scalar | pow (const Scalar &, double) |
Power 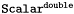 . More... . More... | |
| Scalar | abs (const Scalar &) |
| Absolute value. More... | |
| double | totalmax (const Scalar &) |
Maximum values of a Scalar in each domain. More... | |
| double | totalmin (const Scalar &) |
Minimum values of a Scalar in each domain. More... | |
| Tbl | max (const Scalar &) |
Maximum values of a Scalar in each domain. More... | |
| Tbl | min (const Scalar &) |
Minimum values of a Scalar in each domain. More... | |
| Tbl | norme (const Scalar &) |
Sums of the absolute values of all the values of the Scalar in each domain. More... | |
| Tbl | diffrel (const Scalar &a, const Scalar &b) |
Relative difference between two Scalar (norme version). More... | |
| Tbl | diffrelmax (const Scalar &a, const Scalar &b) |
Relative difference between two Scalar (max version). More... | |
Detailed Description
Tensor field of valence 0 (or component of a tensorial field).
()
Constructor & Destructor Documentation
◆ Scalar() [1/5]
|
explicit |
◆ Scalar() [2/5]
| Lorene::Scalar::Scalar | ( | const Tensor & | a | ) |
Constructor from a Tensor (must be of valence 0)
Definition at line 221 of file scalar.C.
References Lorene::Tensor::cmp, set_der_0x0(), and Lorene::Tensor::valence.
◆ Scalar() [3/5]
| Lorene::Scalar::Scalar | ( | const Scalar & | a | ) |
Copy constructor.
Definition at line 234 of file scalar.C.
References Lorene::Tensor::cmp, and set_der_0x0().
◆ Scalar() [4/5]
| Lorene::Scalar::Scalar | ( | const Cmp & | a | ) |
Constructor by conversion of a Cmp.
Definition at line 244 of file scalar.C.
References Lorene::Tensor::cmp, and set_der_0x0().
◆ Scalar() [5/5]
Constructor from a file (see sauve(FILE*) )
Definition at line 254 of file scalar.C.
References Lorene::Tensor::cmp, dzpuis, etat, Lorene::fread_be(), Lorene::Map::get_mg(), and set_der_0x0().
◆ ~Scalar()
|
virtual |
Member Function Documentation
◆ allocate_all()
|
virtual |
Sets the logical state to ETATQCQ (ordinary state) and performs the memory allocation of all the elements, down to the double arrays of the Tbl s.
This function performs in fact recursive calls to set_etat_qcq() on each element of the chain Scalar -> Valeur -> Mtbl -> Tbl .
Reimplemented from Lorene::Tensor.
Definition at line 371 of file scalar.C.
References Lorene::Valeur::c, Lorene::Mtbl::get_nzone(), Lorene::Valeur::set_etat_c_qcq(), Lorene::Mtbl::set_etat_qcq(), Lorene::Tbl::set_etat_qcq(), set_etat_qcq(), Lorene::Mtbl::t, and va.
◆ annule()
|
virtual |
Sets the Scalar to zero in several domains.
- Parameters
-
l_min [input] The Scalarwill be set (logically) to zero in the domains whose indices are in the range[l_min,l_max] .l_max [input] see the comments for l_min.
Note that annule(0,va.mg->get_nzone()-1) is equivalent to set_etat_zero() .
Reimplemented from Lorene::Tensor.
Definition at line 397 of file scalar.C.
References etat, Lorene::Mg3d::get_nzone(), Lorene::Valeur::mg, set_etat_zero(), and va.
◆ annule_domain()
|
inherited |
Sets the Tensor to zero in a given domain.
- Parameters
-
l [input] Index of the domain in which the Tensorwill be set (logically) to zero.
Definition at line 676 of file tensor.C.
References Lorene::Tensor::annule().
◆ annule_extern_cn()
|
inherited |
Performs a smooth (C^n) transition in a given domain to zero.
- Parameters
-
l_0 [input] in the domain of index l0 the tensor is multiplied by the right polynomial (of degree 2n+1), to ensure continuty of the function and its n first derivative at both ends of this domain. The tensor is unchanged in the domains l < l_0 and set to zero in domains l > l_0. deg [input] the degree n of smoothness of the transition.
Definition at line 700 of file tensor.C.
References Lorene::Map::get_mg(), Lorene::Mg3d::get_type_r(), and Lorene::Tensor::mp.
◆ annule_hard()
| void Lorene::Scalar::annule_hard | ( | ) |
Sets the Scalar to zero in a hard way.
1/ Sets the logical state to ETATQCQ , i.e. to an ordinary state. 2/ Fills the Valeur va with zeros. NB: this function must be used for debugging purposes only. For other operations, the functions set_etat_zero() or annule(int,int) must be perferred.
Definition at line 386 of file scalar.C.
References Lorene::Valeur::annule_hard(), del_deriv(), etat, and va.
◆ annule_l()
| void Lorene::Scalar::annule_l | ( | int | l_min, |
| int | l_max, | ||
| bool | ylm_output = false |
||
| ) |
Sets all the multipolar components between l_min and l_max to zero.
This is done for [ l_min , l_max ] and all relevant m in the spherical harmonics expansion basis. If ylm_output is set to true , then the spectral expansion basis of this is left to be that of spherical harmonics.
Definition at line 123 of file scalar_manip.C.
References etat.
◆ asymptot()
| Valeur ** Lorene::Scalar::asymptot | ( | int | n, |
| const int | flag = 0 |
||
| ) | const |
Asymptotic expansion at r = infinity.
Determines the coefficients 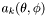 of the expansion
of the expansion
![\[ \sum_{k=0}^n {a_k(\theta, \phi) \over r^k} \]](form_150.png)
of *this when 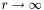 .
.
- Parameters
-
n order of the expansion flag : output
- Returns
- Array of
n+1Valeurs onmg->angu
describing the coefficients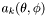 . This array is allocated by the routine.
. This array is allocated by the routine.
Definition at line 66 of file scalar_asymptot.C.
References Lorene::Map::get_mg(), Lorene::Mg3d::get_nzone(), Lorene::Mg3d::get_type_r(), and Lorene::Tensor::mp.
◆ avance_dalembert()
| Scalar Lorene::Scalar::avance_dalembert | ( | Param & | par, |
| const Scalar & | fJm1, | ||
| const Scalar & | source | ||
| ) | const |
Performs one time-step integration (from 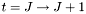 ) of the scalar d'Alembert equation with
) of the scalar d'Alembert equation with *this being the value of the function f at time J .
Works only with an affine mapping (class Map_af ) and, if the last domain is a compactified one, it simply copies the value of the field in this last domain at the time-step J to the last domain of the returned solution.
- Parameters
-
par [input/output] possible parameters to control the resolution of the d'Alembert equation: par.get_double(0): [input] the time step dt ,par.get_int(0): [input] the type of boundary conditions set at the outer boundary (0 : reflexion, 1 : Sommerfeld outgoing wave, valid only for l=0 components, 2 : Bayliss & Turkel outgoing wave, valid for l=0, 1, 2 components)par.get_int_mod(0): [input/output] set to 0 at first call, is used as a working flag after (must not be modified after first call)par.get_tensor_mod(0): [input] (optional) if the wave equation is on a curved space-time, this is the potential in front of the Laplace operator. It has to be a Scalar and updated at every time-step (for a potential depending on time). Note: there are many other working objects attached to thisParam, so one should not modify it. There should be exactly oneParamfor each wave equation to be solved.
fJm1 [input] solution 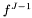 at time J-1
at time J-1 source [input] source  of the d'Alembert equation
of the d'Alembert equation 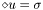 .
.
- Returns
- solution
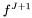 at time J+1 with boundary conditions defined by
at time J+1 with boundary conditions defined by par.get_int(0).
Definition at line 206 of file scalar_pde.C.
References Lorene::Map::dalembert(), and Lorene::Tensor::mp.
◆ change_triad()
|
virtual |
Sets a new vectorial basis (triad) of decomposition and modifies the components accordingly.
Reimplemented from Lorene::Tensor.
◆ check_dzpuis()
| bool Lorene::Scalar::check_dzpuis | ( | int | dzi | ) | const |
Returns false if the last domain is compactified and *this is not zero in this domain and dzpuis is not equal to dzi , otherwise return true.
Definition at line 879 of file scalar.C.
References dz_nonzero(), and dzpuis.
◆ compute_derive_lie()
|
protectedinherited |
Computes the Lie derivative of this with respect to some vector field v (protected method; the public interface is method derive_lie ).
Definition at line 342 of file tensor_calculus.C.
References Lorene::Tensor::cmp, Lorene::contract(), dec_dzpuis(), Lorene::Tensor::derive_cov(), Lorene::Map::flat_met_cart(), Lorene::Map::flat_met_spher(), get_dzpuis(), Lorene::Tensor::get_n_comp(), Lorene::Tensor::get_triad(), Lorene::Tensor::indices(), Lorene::Tensor::mp, Lorene::Tensor::n_comp, Lorene::Tensor::operator()(), Lorene::Itbl::set(), Lorene::Tensor::set(), Lorene::Tensor::triad, Lorene::Tensor::type_indice, and Lorene::Tensor::valence.
◆ copy_coefs_from_large_grid()
| void Lorene::Scalar::copy_coefs_from_large_grid | ( | const Scalar & | scal_large_grid | ) |
Copies the content of the argument Scalar to this defined on a smaller grid, with similar mappings.
It copies the coefficients, discarding the additional ones. Used for de-aliasing purposes.
- Parameters
-
scal_large_grid [input] Scalarto be copied, defined on the larger grid.
Definition at line 590 of file scalar_manip.C.
References etat, Lorene::Map::get_mg(), Lorene::Tensor::get_mp(), Lorene::Mg3d::get_nzone(), get_spectral_base(), and Lorene::Tensor::mp.
◆ copy_coefs_from_larger_grid()
|
inherited |
Copies the content of the argument Tensor to this defined on a smaller grid, with similar mappings.
It copies the coefficients, discarding the additional ones. Used for de-aliasing purposes.
- Parameters
-
tens_small_grid [input] Tensorto be copied, defined on the larger grid.
Definition at line 1123 of file tensor.C.
References Lorene::Tensor::cmp, copy_coefs_from_large_grid(), and Lorene::Tensor::n_comp.
◆ copy_coefs_from_small_grid()
| void Lorene::Scalar::copy_coefs_from_small_grid | ( | const Scalar & | scal_small_grid | ) |
Copies the content of the argument Scalar to this defined on a larger grid, with similar mappings.
It copies the coefficients, setting the additional ones to zero. Used for de-aliasing purposes.
- Parameters
-
scal_small_grid [input] Scalarto be copied, defined on the smaller grid.
Definition at line 505 of file scalar_manip.C.
References etat, Lorene::Map::get_mg(), Lorene::Tensor::get_mp(), Lorene::Mg3d::get_nzone(), get_spectral_base(), and Lorene::Tensor::mp.
◆ copy_coefs_from_smaller_grid()
|
inherited |
Copies the content of the argument Tensor to this defined on a larger grid, with similar mappings.
It copies the coefficients, setting the additional ones to zero. Used for de-aliasing purposes.
- Parameters
-
tens_small_grid [input] Tensorto be copied, defined on the smaller grid.
Definition at line 1116 of file tensor.C.
References Lorene::Tensor::cmp, copy_coefs_from_small_grid(), and Lorene::Tensor::n_comp.
◆ dec_dzpuis()
|
virtual |
Decreases by dec units the value of dzpuis and changes accordingly the values of the Scalar in the compactified external domain (CED).
Reimplemented from Lorene::Tensor.
Definition at line 423 of file scalar_r_manip.C.
References etat.
◆ del_deriv()
|
protectedvirtual |
Logical destructor of the derivatives.
Reimplemented from Lorene::Tensor.
Definition at line 293 of file scalar.C.
References Lorene::Tensor::del_deriv(), p_dsdr, p_dsdradial, p_dsdrho, p_dsdt, p_dsdx, p_dsdy, p_dsdz, p_integ, p_lap, p_lapang, p_srdsdt, p_srstdsdp, p_stdsdp, and set_der_0x0().
◆ del_derive_met()
|
protectedvirtualinherited |
Logical destructor of the derivatives depending on the i-th element of met_depend .
Reimplemented in Lorene::Sym_tensor, and Lorene::Vector.
Definition at line 424 of file tensor.C.
References Lorene::Tensor::met_depend, Lorene::Tensor::p_derive_con, Lorene::Tensor::p_derive_cov, Lorene::Tensor::p_divergence, Lorene::Tensor::set_der_met_0x0(), and Lorene::Metric::tensor_depend.
◆ del_t()
|
protected |
Logical destructor.
Definition at line 285 of file scalar.C.
References del_deriv(), Lorene::Valeur::del_t(), Lorene::Valeur::set_etat_nondef(), and va.
◆ deriv()
| const Scalar & Lorene::Scalar::deriv | ( | int | i | ) | const |
◆ derive_con()
Returns the "contravariant" derivative of *this with respect to some metric  , by raising the index of the gradient (cf.
, by raising the index of the gradient (cf.
method derive_cov() ) with  .
.
Definition at line 401 of file scalar_deriv.C.
References Lorene::Tensor::derive_con().
◆ derive_cov()
Returns the gradient (1-form = covariant vector) of *this
- Parameters
-
gam metric components only used to get the triad with respect to which the components of the result are defined
Definition at line 389 of file scalar_deriv.C.
References Lorene::Tensor::derive_cov().
◆ derive_lie()
Computes the derivative of this along a vector field v.
Definition at line 418 of file scalar_deriv.C.
References Lorene::Tensor::compute_derive_lie(), and Lorene::Tensor::mp.
◆ div_cost()
| void Lorene::Scalar::div_cost | ( | ) |
Division by 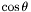 .
.
Definition at line 73 of file scalar_th_manip.C.
References del_deriv(), Lorene::Map::div_cost(), and Lorene::Tensor::mp.
◆ div_r()
| void Lorene::Scalar::div_r | ( | ) |
Division by r everywhere; dzpuis is not changed.
Definition at line 138 of file scalar_r_manip.C.
References del_deriv(), Lorene::Map::div_r(), and Lorene::Tensor::mp.
◆ div_r_ced()
| void Lorene::Scalar::div_r_ced | ( | ) |
Division by r in the compactified external domain (CED), the dzpuis flag is not changed.
Definition at line 201 of file scalar_r_manip.C.
References del_deriv(), Lorene::Map::div_r_zec(), and Lorene::Tensor::mp.
◆ div_r_dzpuis()
| void Lorene::Scalar::div_r_dzpuis | ( | int | ced_mult_r | ) |
Division by r everywhere but with the output flag dzpuis
set to ced_mult_r .
- Parameters
-
ced_mult_r [input] value of dzpuisof the result.
Definition at line 152 of file scalar_r_manip.C.
References etat.
◆ div_rsint()
| void Lorene::Scalar::div_rsint | ( | ) |
Division by 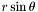 everywhere;
everywhere; dzpuis is not changed.
Definition at line 353 of file scalar_r_manip.C.
References del_deriv(), Lorene::Map::div_rsint(), and Lorene::Tensor::mp.
◆ div_rsint_dzpuis()
| void Lorene::Scalar::div_rsint_dzpuis | ( | int | ced_mult_r | ) |
Division by 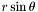 but with the output flag
but with the output flag dzpuis set to ced_mult_r .
- Parameters
-
ced_mult_r [input] value of dzpuisof the result.
Definition at line 367 of file scalar_r_manip.C.
References etat.
◆ div_sint()
| void Lorene::Scalar::div_sint | ( | ) |
Division by 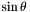 .
.
Definition at line 101 of file scalar_th_manip.C.
References del_deriv(), Lorene::Map::div_sint(), and Lorene::Tensor::mp.
◆ div_tant()
| void Lorene::Scalar::div_tant | ( | ) |
Division by 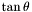 .
.
Definition at line 114 of file scalar_th_manip.C.
References del_deriv(), Lorene::Map::div_tant(), and Lorene::Tensor::mp.
◆ divergence()
Computes the divergence of this with respect to some metric  .
.
The divergence is taken with respect of the last index of this which thus must be contravariant. For instance if the tensor 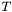 represented by
represented by this is a twice contravariant tensor, whose components w.r.t. the triad 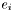 are
are 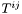 :
: 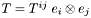 , the divergence of
, the divergence of 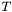 w.r.t.
w.r.t.  is the vector
is the vector
![\[ {\rm div}\, T = \nabla_k T^{ik} \; e_i \]](form_181.png)
where 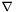 denotes the connection associated with the metric
denotes the connection associated with the metric  .
.
- Parameters
-
gam metric 
- Returns
- divergence of
thiswith respect to .
.
Definition at line 1065 of file tensor.C.
References Lorene::Metric::connect(), Lorene::Tensor::get_place_met(), Lorene::Connection::p_divergence(), Lorene::Tensor::p_divergence, and Lorene::Tensor::set_dependance().
◆ domain()
|
inline |
◆ down()
Computes a new tensor by lowering an index of *this.
- Parameters
-
ind index to be lowered, with the following convention : ind1= 0 : first index of the tensorind1= 1 : second index of the tensor- and so on... (
indmust be of covariant type (CON)).
gam metric used to lower the index (contraction with the twice covariant form of the metric on the index ind).
Definition at line 268 of file tensor_calculus.C.
References Lorene::contract(), Lorene::Metric::cov(), Lorene::Tensor::indices(), Lorene::Tensor::mp, Lorene::Tensor::n_comp, Lorene::Itbl::set(), Lorene::Tensor::set(), Lorene::Tensor::triad, Lorene::Tensor::type_indice, and Lorene::Tensor::valence.
◆ dsdr()
| const Scalar & Lorene::Scalar::dsdr | ( | ) | const |
Returns 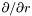 of
of *this .
If dzpuis is zero, then the returned Scalar has dzpuis = 2. It is increased by 1 otherwise.
Definition at line 112 of file scalar_deriv.C.
References etat.
◆ dsdradial()
| const Scalar & Lorene::Scalar::dsdradial | ( | ) | const |
◆ dsdrho()
| const Scalar & Lorene::Scalar::dsdrho | ( | ) | const |
Returns 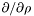 of
of *this .
If dzpuis is zero, then the returned Scalar has dzpuis = 2. It is increased by 1 otherwise.
Definition at line 521 of file scalar_deriv.C.
References etat.
◆ dsdt()
| const Scalar & Lorene::Scalar::dsdt | ( | ) | const |
◆ dsdx()
| const Scalar & Lorene::Scalar::dsdx | ( | ) | const |
Returns 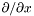 of
of *this , where 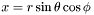 .
.
If dzpuis is zero, then the returned Scalar has dzpuis = 2. It is increased by 1 otherwise.
Definition at line 265 of file scalar_deriv.C.
References etat.
◆ dsdy()
| const Scalar & Lorene::Scalar::dsdy | ( | ) | const |
Returns 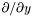 of
of *this , where 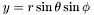 .
.
If dzpuis is zero, then the returned Scalar has dzpuis = 2. It is increased by 1 otherwise.
Definition at line 296 of file scalar_deriv.C.
References etat.
◆ dsdz()
| const Scalar & Lorene::Scalar::dsdz | ( | ) | const |
Returns 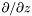 of
of *this , where 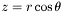 .
.
If dzpuis is zero, then the returned Scalar has dzpuis = 2. It is increased by 1 otherwise.
Definition at line 327 of file scalar_deriv.C.
References etat.
◆ dz_nonzero()
| bool Lorene::Scalar::dz_nonzero | ( | ) | const |
◆ exp_filter_r_all_domains()
| void Lorene::Scalar::exp_filter_r_all_domains | ( | Scalar & | ss, |
| int | p, | ||
| double | alpha = -16. |
||
| ) |
Applies an exponential filter in radial direction in all domains.
(see Scalar:exponential_filter_r ). Note that this may cause regularity problems at the origin if applied in a nucleus.
◆ exponential_filter_r()
|
virtual |
Applies an exponential filter to the spectral coefficients in the radial direction.
The filter is of the type: 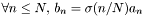 , with
, with 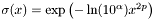 and N the number of radial coefficients.
and N the number of radial coefficients.
- Parameters
-
lzmin,lzmax [input] the indices of the domain where the filter is applied (in [ lzmin,lzmax])p [input] the order of the filter alpha [input] 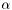 appearing in the above formula.
appearing in the above formula.
Reimplemented from Lorene::Tensor.
Definition at line 72 of file scalar_exp_filter.C.
References etat, Lorene::Map::get_mg(), Lorene::Mg3d::get_nzone(), and Lorene::Tensor::mp.
◆ exponential_filter_ylm()
|
virtual |
Applies an exponential filter to the spectral coefficients in the angular directions.
The filter is of the type: 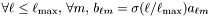 , with
, with 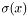 defined for
defined for Scalar::exponential_filter_r and 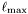 the number of spherical harmonics used.
the number of spherical harmonics used.
Reimplemented from Lorene::Tensor.
Definition at line 154 of file scalar_exp_filter.C.
References etat, Lorene::Map::get_mg(), Lorene::Mg3d::get_nzone(), and Lorene::Tensor::mp.
◆ exponential_filter_ylm_phi()
|
virtual |
Applies an exponential filter to the spectral coefficients in the angular directions.
The filter is of the type: 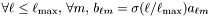 , with
, with 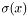 defined for
defined for Scalar::exponential_filter_r and 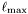 the number of spherical harmonics used.
the number of spherical harmonics used.
Reimplemented from Lorene::Tensor.
Definition at line 198 of file scalar_exp_filter.C.
References etat, Lorene::Map::get_mg(), Lorene::Mg3d::get_nzone(), and Lorene::Tensor::mp.
◆ filtre()
| void Lorene::Scalar::filtre | ( | int | n | ) |
Sets the n lasts coefficients in r to 0 in the external domain.
Definition at line 163 of file scalar_manip.C.
References etat.
◆ filtre_phi()
| void Lorene::Scalar::filtre_phi | ( | int | n, |
| int | zone | ||
| ) |
Sets the n lasts coefficients in 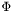 to 0 in the domain
to 0 in the domain zone .
Definition at line 261 of file scalar_manip.C.
References etat.
◆ filtre_r() [1/2]
| void Lorene::Scalar::filtre_r | ( | int * | nn | ) |
Sets the n lasts coefficients in r to 0 in all domains.
Definition at line 192 of file scalar_manip.C.
References etat.
◆ filtre_r() [2/2]
| void Lorene::Scalar::filtre_r | ( | int | n, |
| int | nzone | ||
| ) |
Sets the n last coefficients in r to 0 in the domain nzone .
Definition at line 230 of file scalar_manip.C.
References etat.
◆ filtre_tp()
| void Lorene::Scalar::filtre_tp | ( | int | nn, |
| int | nz1, | ||
| int | nz2 | ||
| ) |
Sets the n lasts coefficients in  to 0 in the domain
to 0 in the domain nz1 to nz2 when expressed in spherical harmonics.
Definition at line 282 of file scalar_manip.C.
References Lorene::Valeur::filtre_tp(), and va.
◆ fixe_decroissance()
| void Lorene::Scalar::fixe_decroissance | ( | int | puis | ) |
Substracts all the components behaving like 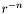 in the external domain, with n strictly lower than
in the external domain, with n strictly lower than puis , so that *this
decreases at least like 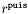 at infinity.
at infinity.
Definition at line 358 of file scalar_manip.C.
References Lorene::Valeur::base, Lorene::Valeur::c_cf, Lorene::Valeur::coef(), cos, dzpuis, Lorene::Map_af::get_alpha(), Lorene::Base_val::get_base_r(), Lorene::Map::get_mg(), Lorene::Mg3d::get_np(), Lorene::Mg3d::get_nr(), Lorene::Mg3d::get_nt(), Lorene::Mg3d::get_nzone(), Lorene::Tensor::mp, mult_r_ced(), pow, R_CHEBU, Lorene::Mtbl_cf::set(), Lorene::Valeur::set_etat_cf_qcq(), and va.
◆ get_dzpuis()
|
inline |
◆ get_etat()
|
inline |
◆ get_index_type() [1/2]
|
inlineinherited |
Gives the type (covariant or contravariant) of the index number i .
i must be strictly lower than valence and obey the following convention:
i= 0 : first indexi= 1 : second index- and so on...
- Returns
- COV for a covariant index, CON for a contravariant one.
Definition at line 927 of file tensor.h.
References Lorene::Tensor::type_indice.
◆ get_index_type() [2/2]
|
inlineinherited |
Returns the types of all the indices.
- Returns
- 1-D array of integers (class
Itbl) of sizevalence
containing the type of each index,COVfor a covariant one andCON
for a contravariant one.
Definition at line 937 of file tensor.h.
References Lorene::Tensor::type_indice.
◆ get_mp()
|
inlineinherited |
◆ get_n_comp()
|
inlineinherited |
Returns the number of stored components.
Definition at line 913 of file tensor.h.
References Lorene::Tensor::n_comp.
◆ get_place_met()
|
protectedinherited |
Returns the position of the pointer on metre in the array met_depend .
Definition at line 453 of file tensor.C.
References Lorene::Tensor::met_depend.
◆ get_spectral_base()
|
inline |
Returns the spectral bases of the Valeur va.
Definition at line 1356 of file scalar.h.
References Lorene::Valeur::base, and va.
◆ get_spectral_va()
|
inline |
◆ get_triad()
|
inlineinherited |
Returns the vectorial basis (triad) on which the components are defined.
Definition at line 907 of file tensor.h.
References Lorene::Tensor::triad.
◆ get_valence()
|
inlineinherited |
◆ import() [1/2]
| void Lorene::Scalar::import | ( | const Scalar & | ci | ) |
Assignment to another Scalar defined on a different mapping.
This assignment is performed point to point by means of the spectral expansion of the original Scalar.
- Parameters
-
ci [input] Scalarto be imported.
Definition at line 71 of file scalar_import.C.
References Lorene::Map::get_mg(), Lorene::Mg3d::get_nzone(), and Lorene::Tensor::mp.
◆ import() [2/2]
| void Lorene::Scalar::import | ( | int | nzet, |
| const Scalar & | ci | ||
| ) |
Assignment to another Scalar defined on a different mapping.
This assignment is performed point to point by means of the spectral expansion of the original Scalar.
- Parameters
-
nzet [input] Number of domains of the destination mapping (i.e. this->mp) where the importation is performed: the assignment is done for the domains whose indices are between 0 andnzet-1. In the other domains,*thisis set to zero.ci [input] Scalarto be imported.
Definition at line 83 of file scalar_import.C.
References Lorene::Map::get_bvect_cart(), Lorene::Tensor::get_mp(), import_align(), import_anti(), import_gal(), and Lorene::Tensor::mp.
◆ import_align()
|
protected |
Assignment to another Scalar defined on a different mapping, when the two mappings have aligned Cartesian axis.
This assignment is performed point to point by means of the spectral expansion of the original Scalar.
- Parameters
-
nzet [input] Number of domains of the destination mapping (i.e. this->mp) where the importation is performed: the assignment is done for the domains whose indices are between 0 andnzet-1. In the other domains,*thisis set to zero.ci [input] Scalarto be imported.
Definition at line 535 of file scalar_import.C.
References get_etat().
◆ import_align_asymy()
|
protected |
Assignment to another Scalar defined on a different mapping, when the two mappings have aligned Cartesian axis.
Case where the Scalar is antisymmetric with respect to the plane y=0.
This assignment is performed point to point by means of the spectral expansion of the original Scalar.
- Parameters
-
nzet [input] Number of domains of the destination mapping (i.e. this->mp) where the importation is performed: the assignment is done for the domains whose indices are between 0 andnzet-1. In the other domains,*thisis set to zero.ci [input] Scalarto be imported.
Definition at line 381 of file scalar_import_asymy.C.
References get_etat().
◆ import_align_symy()
|
protected |
Assignment to another Scalar defined on a different mapping, when the two mappings have aligned Cartesian axis.
Case where the Scalar is symmetric with respect to the plane y=0.
This assignment is performed point to point by means of the spectral expansion of the original Scalar.
- Parameters
-
nzet [input] Number of domains of the destination mapping (i.e. this->mp) where the importation is performed: the assignment is done for the domains whose indices are between 0 andnzet-1. In the other domains,*thisis set to zero.ci [input] Scalarto be imported.
Definition at line 352 of file scalar_import_symy.C.
References get_etat().
◆ import_anti()
|
protected |
Assignment to another Scalar defined on a different mapping, when the two mappings have anti-aligned Cartesian axis (i.e.
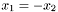 ,
, 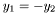 ,
, 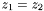 ).
).
This assignment is performed point to point by means of the spectral expansion of the original Scalar.
- Parameters
-
nzet [input] Number of domains of the destination mapping (i.e. this->mp) where the importation is performed: the assignment is done for the domains whose indices are between 0 andnzet-1. In the other domains,*thisis set to zero.ci [input] Scalarto be imported.
Definition at line 338 of file scalar_import.C.
References get_etat().
◆ import_anti_asymy()
|
protected |
Assignment to another Scalar defined on a different mapping, when the two mappings have anti-aligned Cartesian axis (i.e.
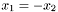 ,
, 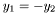 ,
, 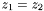 ). Case where the
). Case where the Scalar is antisymmetric with respect to the plane y=0.
This assignment is performed point to point by means of the spectral expansion of the original Scalar.
- Parameters
-
nzet [input] Number of domains of the destination mapping (i.e. this->mp) where the importation is performed: the assignment is done for the domains whose indices are between 0 andnzet-1. In the other domains,*thisis set to zero.ci [input] Scalarto be imported.
Definition at line 134 of file scalar_import_asymy.C.
References get_etat().
◆ import_anti_symy()
|
protected |
Assignment to another Scalar defined on a different mapping, when the two mappings have anti-aligned Cartesian axis (i.e.
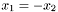 ,
, 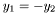 ,
, 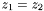 ). Case where the
). Case where the Scalar is symmetric with respect to the plane y=0.
This assignment is performed point to point by means of the spectral expansion of the original Scalar.
- Parameters
-
nzet [input] Number of domains of the destination mapping (i.e. this->mp) where the importation is performed: the assignment is done for the domains whose indices are between 0 andnzet-1. In the other domains,*thisis set to zero.ci [input] Scalarto be imported.
Definition at line 134 of file scalar_import_symy.C.
References get_etat().
◆ import_asymy() [1/2]
| void Lorene::Scalar::import_asymy | ( | const Scalar & | ci | ) |
Assignment to another Scalar defined on a different mapping.
Case where the Scalar is antisymmetric with respect to the plane y=0. This assignment is performed point to point by means of the spectral expansion of the original Scalar.
- Parameters
-
ci [input] Scalarto be imported.
Definition at line 75 of file scalar_import_asymy.C.
References Lorene::Map::get_mg(), Lorene::Mg3d::get_nzone(), and Lorene::Tensor::mp.
◆ import_asymy() [2/2]
| void Lorene::Scalar::import_asymy | ( | int | nzet, |
| const Scalar & | ci | ||
| ) |
Assignment to another Scalar defined on a different mapping.
Case where the Scalar is antisymmetric with respect to the plane y=0. This assignment is performed point to point by means of the spectral expansion of the original Scalar.
- Parameters
-
nzet [input] Number of domains of the destination mapping (i.e. this->mp) where the importation is performed: the assignment is done for the domains whose indices are between 0 andnzet-1. In the other domains,*thisis set to zero.ci [input] Scalarto be imported.
Definition at line 87 of file scalar_import_asymy.C.
References Lorene::Map::get_bvect_cart(), Lorene::Tensor::get_mp(), import_align_asymy(), import_anti_asymy(), and Lorene::Tensor::mp.
◆ import_gal()
|
protected |
Assignment to another Scalar defined on a different mapping, when the two mappings do not have a particular relative orientation.
This assignment is performed point to point by means of the spectral expansion of the original Scalar.
- Parameters
-
nzet [input] Number of domains of the destination mapping (i.e. this->mp) where the importation is performed: the assignment is done for the domains whose indices are between 0 andnzet-1. In the other domains,*thisis set to zero.ci [input] Scalarto be imported.
Definition at line 134 of file scalar_import.C.
References get_etat(), Lorene::Tensor::get_mp(), and Lorene::Tensor::mp.
◆ import_symy() [1/2]
| void Lorene::Scalar::import_symy | ( | const Scalar & | ci | ) |
Assignment to another Scalar defined on a different mapping.
Case where the Scalar is symmetric with respect to the plane y=0. This assignment is performed point to point by means of the spectral expansion of the original Scalar.
- Parameters
-
ci [input] Scalarto be imported.
Definition at line 75 of file scalar_import_symy.C.
References Lorene::Map::get_mg(), Lorene::Mg3d::get_nzone(), and Lorene::Tensor::mp.
◆ import_symy() [2/2]
| void Lorene::Scalar::import_symy | ( | int | nzet, |
| const Scalar & | ci | ||
| ) |
Assignment to another Scalar defined on a different mapping.
Case where the Scalar is symmetric with respect to the plane y=0. This assignment is performed point to point by means of the spectral expansion of the original Scalar.
- Parameters
-
nzet [input] Number of domains of the destination mapping (i.e. this->mp) where the importation is performed: the assignment is done for the domains whose indices are between 0 andnzet-1. In the other domains,*thisis set to zero.ci [input] Scalarto be imported.
Definition at line 87 of file scalar_import_symy.C.
References Lorene::Map::get_bvect_cart(), Lorene::Tensor::get_mp(), import_align_symy(), import_anti_symy(), and Lorene::Tensor::mp.
◆ inc_dzpuis()
|
virtual |
Increases by inc units the value of dzpuis and changes accordingly the values of the Scalar in the compactified external domain (CED).
Reimplemented from Lorene::Tensor.
Definition at line 475 of file scalar_r_manip.C.
References etat.
◆ indices()
|
virtualinherited |
Returns the indices of a component given by its position in the array cmp .
- Parameters
-
pos [input] position in the array cmpof the pointer to theScalarrepresenting a component
- Returns
- 1-D array of integers (class
Itbl) of sizevalencegiving the value of each index for the component located at the positionposin the arraycmp, with the following storage convention:Itbl(0): value of the first index (1, 2 or 3)Itbl(1): value of the second index (1, 2 or 3)- and so on...
Reimplemented in Lorene::Tensor_sym, and Lorene::Vector.
Definition at line 549 of file tensor.C.
References Lorene::Tensor::n_comp, Lorene::Itbl::set(), and Lorene::Tensor::valence.
◆ integrale()
| double Lorene::Scalar::integrale | ( | ) | const |
Computes the integral over all space of *this .
The computed quantity is (u being the field represented by *this ) 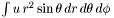 . Note that in the compactified external domain (CED),
. Note that in the compactified external domain (CED), dzpuis
must be 4 for the computation to take place.
Definition at line 67 of file scalar_integ.C.
References Lorene::Map::get_mg(), Lorene::Mg3d::get_nzone(), integrale_domains(), and Lorene::Tensor::mp.
◆ integrale_domains()
| const Tbl & Lorene::Scalar::integrale_domains | ( | ) | const |
Computes the integral in each domain of *this .
The computed quantity is (u being the field represented by *this ) 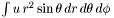 in each domain. The result is returned a
in each domain. The result is returned a Tbl on the various domains. Note that in the compactified external domain (CED), dzpuis
must be 4 for the computation to take place.
Definition at line 85 of file scalar_integ.C.
References etat.
◆ is_nan()
| bool Lorene::Scalar::is_nan | ( | bool | verbose = false | ) | const |
◆ lapang()
| const Scalar & Lorene::Scalar::lapang | ( | ) | const |
Returns the angular Laplacian 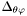 of
of *this , where 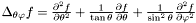 .
.
Definition at line 460 of file scalar_deriv.C.
References etat.
◆ laplacian()
| const Scalar & Lorene::Scalar::laplacian | ( | int | ced_mult_r = 4 | ) | const |
Returns the Laplacian of *this.
- Parameters
-
ced_mult_r [input] Determines the quantity computed in the compactified external domain (CED) (u in the field represented by *this) :
- ced_mult_r = 0 :
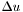
- ced_mult_r = 2 :
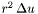
- ced_mult_r = 4 (default) :
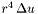
- ced_mult_r = 0 :
Definition at line 435 of file scalar_deriv.C.
References etat.
◆ match_collocation()
Method for matching accross domains and imposing boundary condition.
Matching of the field represented by this accross domains and imposition of the boundary condition using the collocation method.
◆ match_tau()
Method for matching accross domains and imposing boundary condition.
Matching of the field represented by this accross domains and imposition of the boundary condition using the tau method.
- Parameters
-
par_bc [input] Paramto control the boundary conditions par_bc must contain (at a minimum) a modifiable Tbl which specifies a physical boundary two integers, one specifying the domain that has the boundary the other specifying the number of conditions 1 -> Dirichlet 2 -> Robin (which may reduce to von Neumann, see below) two doubles, specifying the Robin BC parameters. If the first is zero, we see that Robin will reduce to von Neumannpar_mat [input/output] optional Paramin which the matching matrices are stored (together with their LU decomposition).
Definition at line 75 of file scalar_match_tau.C.
References Lorene::Map::get_mg(), Lorene::Mg3d::get_type_r(), and Lorene::Tensor::mp.
◆ match_tau_shell()
Method for matching accross domains and imposing boundary condition.
Matching of the field represented by this accross domains and imposition of the boundary condition using the tau method.
◆ match_tau_star()
Method for matching accross domains and imposing boundary condition.
Matching of the field represented by this accross domains and imposition of the boundary condition using the tau method for a grid with Map_star mapping.
- Parameters
-
par_bc [input] Paramto control the boundary conditions par_bc must contain (at a minimum) a modifiable Tbl which specifies a physical boundary two integers, one specifying the domain that has the boundary the other specifying the number of conditions 1 -> Dirichlet 2 -> Robin (which may reduce to von Neumann, see below) two doubles, specifying the Robin BC parameters. If the first is zero, we see that Robin will reduce to von Neumannpar_mat [input/output] optional Paramin which the matching matrices are stored (together with their LU decomposition).
Definition at line 591 of file scalar_match_tau.C.
References Lorene::Map::get_mg(), Lorene::Mg3d::get_type_r(), and Lorene::Tensor::mp.
◆ mult_cost()
| void Lorene::Scalar::mult_cost | ( | ) |
Multiplication by 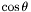 .
.
Definition at line 61 of file scalar_th_manip.C.
References del_deriv(), Lorene::Tensor::mp, and Lorene::Map::mult_cost().
◆ mult_r()
| void Lorene::Scalar::mult_r | ( | ) |
Multiplication by r everywhere; dzpuis is not changed.
Definition at line 213 of file scalar_r_manip.C.
References del_deriv(), Lorene::Tensor::mp, and Lorene::Map::mult_r().
◆ mult_r_ced()
| void Lorene::Scalar::mult_r_ced | ( | ) |
Multiplication by r in the compactified external domain (CED), the dzpuis flag is not changed.
Definition at line 274 of file scalar_r_manip.C.
References del_deriv(), Lorene::Tensor::mp, and Lorene::Map::mult_r_zec().
◆ mult_r_dzpuis()
| void Lorene::Scalar::mult_r_dzpuis | ( | int | ced_mult_r | ) |
Multiplication by r everywhere but with the output flag dzpuis
set to ced_mult_r .
- Parameters
-
ced_mult_r [input] value of dzpuisof the result.
Definition at line 226 of file scalar_r_manip.C.
References etat.
◆ mult_rsint()
| void Lorene::Scalar::mult_rsint | ( | ) |
Multiplication by 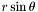 everywhere;
everywhere; dzpuis is not changed.
Definition at line 286 of file scalar_r_manip.C.
References del_deriv(), Lorene::Tensor::mp, and Lorene::Map::mult_rsint().
◆ mult_rsint_dzpuis()
| void Lorene::Scalar::mult_rsint_dzpuis | ( | int | ced_mult_r | ) |
Multiplication by 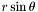 but with the output flag
but with the output flag dzpuis set to ced_mult_r .
- Parameters
-
ced_mult_r [input] value of dzpuisof the result.
Definition at line 299 of file scalar_r_manip.C.
References etat.
◆ mult_sint()
| void Lorene::Scalar::mult_sint | ( | ) |
Multiplication by 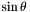 .
.
Definition at line 87 of file scalar_th_manip.C.
References del_deriv(), Lorene::Tensor::mp, and Lorene::Map::mult_sint().
◆ multipole_spectrum()
| Tbl Lorene::Scalar::multipole_spectrum | ( | ) | const |
Gives the spectrum in terms of multipolar modes l .
- Returns
- a
Tblof size (nzone, lmax), where lmax is the maximal multipolar momentum over all domains. The l -th element contains the L1 norm of the l -th multipole (i.e. a sum over all m of the norms (coefficient space) of the component of a given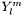 .
.
Definition at line 962 of file scalar.C.
References etat.
◆ operator Cmp()
| Lorene::Scalar::operator Cmp | ( | ) | const |
◆ operator()() [1/4]
Returns the value of a component (read-only version).
- Parameters
-
ind 1-D Itblof sizevalencecontaining the values of each index specifing the component, with the following storage convention:ind(0): value of the first index (1, 2 or 3)ind(1): value of the second index (1, 2 or 3)- and so on...
- Returns
- reference on the component specified by
ind
Definition at line 808 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Itbl::get_dim(), Lorene::Itbl::get_ndim(), Lorene::Tensor::position(), and Lorene::Tensor::valence.
◆ operator()() [2/4]
|
inherited |
Returns the value of a component for a tensor of valence 2 (read-only version).
- Parameters
-
i1 value of the first index (1, 2 or 3) i2 value of the second index (1, 2 or 3)
- Returns
- reference on the component specified by
(i1,i2)
Definition at line 770 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::position(), Lorene::Itbl::set(), and Lorene::Tensor::valence.
◆ operator()() [3/4]
|
inherited |
Returns the value of a component for a tensor of valence 3 (read-only version).
- Parameters
-
i1 value of the first index (1, 2 or 3) i2 value of the second index (1, 2 or 3) i3 value of the third index (1, 2 or 3)
- Returns
- reference on the component specified by
(i1,i2,i3)
Definition at line 781 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::position(), Lorene::Itbl::set(), and Lorene::Tensor::valence.
◆ operator()() [4/4]
|
inherited |
Returns the value of a component for a tensor of valence 4 (read-only version).
- Parameters
-
i1 value of the first index (1, 2 or 3) i2 value of the second index (1, 2 or 3) i3 value of the third index (1, 2 or 3) i4 value of the fourth index (1, 2 or 3)
- Returns
- reference on the component specified by
(i1,i2,i3,i4)
Definition at line 793 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::position(), Lorene::Itbl::set(), and Lorene::Tensor::valence.
◆ operator*=()
| void Lorene::Scalar::operator*= | ( | const Scalar & | ci | ) |
*= Scalar
Definition at line 940 of file scalar_arithm.C.
References etat, Lorene::Tensor::get_mp(), and Lorene::Tensor::mp.
◆ operator+=() [1/2]
|
inherited |
+= Tensor
Definition at line 581 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), Lorene::Tensor::indices(), Lorene::Tensor::n_comp, Lorene::Tensor::position(), Lorene::Tensor::triad, Lorene::Tensor::type_indice, and Lorene::Tensor::valence.
◆ operator+=() [2/2]
| void Lorene::Scalar::operator+= | ( | const Scalar & | ci | ) |
+= Scalar
Definition at line 836 of file scalar_arithm.C.
References etat, Lorene::Tensor::get_mp(), and Lorene::Tensor::mp.
◆ operator-=() [1/2]
|
inherited |
-= Tensor
Definition at line 597 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), Lorene::Tensor::indices(), Lorene::Tensor::n_comp, Lorene::Tensor::position(), Lorene::Tensor::triad, Lorene::Tensor::type_indice, and Lorene::Tensor::valence.
◆ operator-=() [2/2]
| void Lorene::Scalar::operator-= | ( | const Scalar & | ci | ) |
-= Scalar
Definition at line 889 of file scalar_arithm.C.
References etat, Lorene::Tensor::get_mp(), and Lorene::Tensor::mp.
◆ operator=() [1/7]
| void Lorene::Scalar::operator= | ( | const Scalar & | a | ) |
◆ operator=() [2/7]
|
virtual |
Assignment to a Tensor (of valence 0)
Reimplemented from Lorene::Tensor.
Definition at line 442 of file scalar.C.
References Lorene::Tensor::cmp, operator=(), and Lorene::Tensor::valence.
◆ operator=() [3/7]
| void Lorene::Scalar::operator= | ( | const Cmp & | a | ) |
Assignment to a Cmp.
Definition at line 505 of file scalar.C.
References Lorene::Valeur::del_t(), dzpuis, Lorene::Cmp::get_dzpuis(), Lorene::Cmp::get_etat(), Lorene::Cmp::get_mp(), Lorene::Tensor::mp, and va.
◆ operator=() [4/7]
| void Lorene::Scalar::operator= | ( | const Valeur & | a | ) |
Assignment to a Valeur.
Definition at line 555 of file scalar.C.
References Lorene::Valeur::get_etat(), and va.
◆ operator=() [5/7]
| void Lorene::Scalar::operator= | ( | const Mtbl & | a | ) |
◆ operator=() [6/7]
| void Lorene::Scalar::operator= | ( | double | x | ) |
Assignment to a double.
Definition at line 638 of file scalar.C.
References del_deriv(), dzpuis, set_etat_one(), set_etat_qcq(), set_etat_zero(), and va.
◆ operator=() [7/7]
| void Lorene::Scalar::operator= | ( | int | n | ) |
Assignment to an int.
Definition at line 659 of file scalar.C.
References del_deriv(), dzpuis, set_etat_one(), set_etat_qcq(), set_etat_zero(), and va.
◆ poisson() [1/2]
| Scalar Lorene::Scalar::poisson | ( | ) | const |
Solves the scalar Poisson equation with *this as a source.
The source  of the equation
of the equation 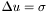 is represented by the
is represented by the Scalar *this . Note that dzpuis must be equal to 2 or 4, i.e. that the quantity stored in *this is in fact 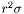 or
or 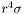 in the compactified external domain. The solution u with the boundary condition u =0 at spatial infinity is the returned
in the compactified external domain. The solution u with the boundary condition u =0 at spatial infinity is the returned Scalar.
Definition at line 139 of file scalar_pde.C.
References Lorene::Tensor::mp, and Lorene::Map::poisson().
◆ poisson() [2/2]
Solves the scalar Poisson equation with *this as a source (version with parameters to control the resolution).
The source  of the equation
of the equation 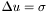 is represented by the
is represented by the Scalar *this . Note that dzpuis must be equal to 2 or 4, i.e. that the quantity stored in *this is in fact 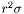 or
or 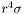 in the compactified external domain.
in the compactified external domain.
- Parameters
-
par [input/output] possible parameters uu [input/output] solution u with the boundary condition u =0 at spatial infinity.
Definition at line 152 of file scalar_pde.C.
References Lorene::Tensor::mp, and Lorene::Map::poisson().
◆ poisson_angu()
| Scalar Lorene::Scalar::poisson_angu | ( | double | lambda = 0 | ) | const |
Solves the (generalized) angular Poisson equation with *this
as source.
The generalized angular Poisson equation is 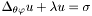 , where
, where 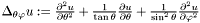 .
.
- Parameters
-
lambda [input] coefficient 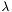 in the above equation (default value = 0)
in the above equation (default value = 0)
- Returns
- solution u .
Definition at line 189 of file scalar_pde.C.
References Lorene::Tensor::mp, and Lorene::Map::poisson_angu().
◆ poisson_dir_neu()
| Scalar Lorene::Scalar::poisson_dir_neu | ( | const Valeur & | limite, |
| int | num, | ||
| double | fact_dir, | ||
| double | fact_neu | ||
| ) | const |
Is identicall to Scalar::poisson() .
The regularity condition at the origin is replace by a mixed boundary condition (Dirichlet + Neumann).
- Parameters
-
limite [input] : angular function. The boundary condition is given by limite[num] .num [input] : index of the boudary at which the condition is to be fullfilled. fact_dir [input] : double in front of 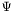 (if
(if  is the variable solved).
is the variable solved). fact_neu [input] : double in front of the radial derivative of  .
.
More precisely we impose 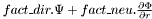 is equal to the source at the boundary between the domains
is equal to the source at the boundary between the domains num and num+1 (the latter one being a shell).
Definition at line 83 of file scalar_pde_frontiere.C.
References Lorene::Tensor::mp, Lorene::Map::poisson_frontiere(), Lorene::Cmp::set_dzpuis(), and Lorene::Cmp::va.
◆ poisson_dirichlet()
Is identicall to Scalar::poisson() .
The regularity condition at the origin is replace by a boundary condition of the Dirichlet type.
- Parameters
-
limite [input] : angular function. The boundary condition is given by limite[num] .num [input] : index of the boudary at which the condition is to be fullfilled.
More precisely we impose the solution is equal to limite[num] at the boundary between the domains num and num+1 (the latter one being a shell).
Definition at line 67 of file scalar_pde_frontiere.C.
References Lorene::Tensor::mp, Lorene::Map::poisson_frontiere(), Lorene::Cmp::set_dzpuis(), and Lorene::Cmp::va.
◆ poisson_frontiere_double()
| Scalar Lorene::Scalar::poisson_frontiere_double | ( | const Valeur & | lim_func, |
| const Valeur & | lim_der, | ||
| int | num_zone | ||
| ) | const |
Idem as Scalar::poisson_dirichlet , the boundary condition being on both the function and its radial derivative.
The boundary condition at infinity is relaxed.
Definition at line 118 of file scalar_pde_frontiere.C.
References Lorene::Tensor::mp.
◆ poisson_neumann()
Idem as Scalar::poisson_dirichlet , the boundary condition being on the radial derivative of the solution.
Definition at line 101 of file scalar_pde_frontiere.C.
References Lorene::Tensor::mp, Lorene::Map::poisson_frontiere(), Lorene::Cmp::set_dzpuis(), and Lorene::Cmp::va.
◆ poisson_regular()
| void Lorene::Scalar::poisson_regular | ( | int | k_div, |
| int | nzet, | ||
| double | unsgam1, | ||
| Param & | par, | ||
| Scalar & | uu, | ||
| Scalar & | uu_regu, | ||
| Scalar & | uu_div, | ||
| Tensor & | duu_div, | ||
| Scalar & | source_regu, | ||
| Scalar & | source_div | ||
| ) | const |
Solves the scalar Poisson equation with *this as a source (version with parameters to control the resolution).
The source  of the equation
of the equation 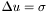 is represented by the
is represented by the Scalar *this . The regularized source 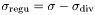 is constructed and solved. Note that
is constructed and solved. Note that dzpuis must be equal to 2 or 4, i.e. that the quantity stored in *this is in fact 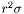 or
or 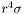 in the compactified external domain.
in the compactified external domain.
- Parameters
-
k_div [input] regularization degree of the procedure nzet [input] number of domains covering the star unsgam1 [input] parameter 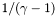 where
where  denotes the adiabatic index
denotes the adiabatic index par [input/output] possible parameters uu [input/output] solution uu_regu [output] solution of the regular part of the source. uu_div [output] solution of the diverging part of the source. duu_div [output] derivative of the diverging potential. source_regu [output] regularized source source_div [output] diverging part of the source
Definition at line 65 of file scalar_poisson_regu.C.
References Lorene::Tensor::get_triad(), Lorene::Tensor::mp, Lorene::Map::poisson_regular(), Lorene::Itbl::set(), Lorene::Tensor::set(), Lorene::Tenseur::set(), Lorene::Itbl::set_etat_qcq(), and Lorene::Tenseur::set_etat_qcq().
◆ poisson_tau() [1/2]
| Scalar Lorene::Scalar::poisson_tau | ( | ) | const |
Solves the scalar Poisson equation with *this as a source using a real Tau method The source  of the equation
of the equation 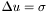 is represented by the
is represented by the Scalar *this .
Note that dzpuis must be equal to 2, 3 or 4, i.e. that the quantity stored in *this is in fact 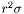 ,
, 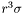 or
or 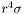 in the compactified external domain. The solution u with the boundary condition u =0 at spatial infinity is the returned
in the compactified external domain. The solution u with the boundary condition u =0 at spatial infinity is the returned Scalar.
Definition at line 165 of file scalar_pde.C.
References Lorene::Tensor::mp, and Lorene::Map::poisson_tau().
◆ poisson_tau() [2/2]
Solves the scalar Poisson equation with *this as a source using a real Tau method (version with parameters to control the resolution) The source  of the equation
of the equation 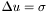 is represented by the
is represented by the Scalar *this .
Note that dzpuis must be equal to 2, 3 or 4, i.e. that the quantity stored in *this is in fact 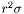 ,
, 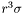 or
or 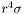 in the compactified external domain. The solution u with the boundary condition u =0 at spatial infinity is the returned
in the compactified external domain. The solution u with the boundary condition u =0 at spatial infinity is the returned Scalar.
Definition at line 177 of file scalar_pde.C.
References Lorene::Tensor::mp, and Lorene::Map::poisson_tau().
◆ position()
|
virtualinherited |
Returns the position in the array cmp of a component given by its indices.
- Parameters
-
ind [input] 1-D array of integers (class Itbl) of sizevalencegiving the values of each index specifing the component, with the following storage convention:ind(0): value of the first index (1, 2 or 3)ind(1): value of the second index (1, 2 or 3)- and so on...
- Returns
- position in the array
cmpof the pointer to theScalarcontaining the component specified byind
Reimplemented in Lorene::Tensor_sym, and Lorene::Vector.
Definition at line 535 of file tensor.C.
References Lorene::Itbl::get_dim(), Lorene::Itbl::get_ndim(), and Lorene::Tensor::valence.
◆ primr()
| Scalar Lorene::Scalar::primr | ( | bool | null_infty = true | ) | const |
Computes the radial primitive which vanishes for 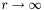 .
.
i.e. the function 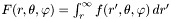 where f is the function represented by
where f is the function represented by *this (and must have a dzpuis = 2).
- Parameters
-
null_infty if true (default), the primitive is null at infinity (or on the grid boundary). F is null at the center otherwise
- Returns
- function F
Definition at line 106 of file scalar_integ.C.
References Lorene::Tensor::mp, and Lorene::Map::primr().
◆ raccord()
| void Lorene::Scalar::raccord | ( | int | n | ) |
Performs the 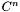 matching of the nucleus with respect to the first shell.
matching of the nucleus with respect to the first shell.
Definition at line 65 of file scalar_raccord.C.
References etat.
◆ raccord_c1_zec()
| void Lorene::Scalar::raccord_c1_zec | ( | int | puis, |
| int | nbre, | ||
| int | lmax | ||
| ) |
Performs the 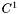 matching of the external domain with respect to the last shell using function like
matching of the external domain with respect to the last shell using function like 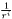 with
with 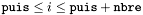 for each spherical harmonics with
for each spherical harmonics with 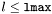 .
.
Definition at line 80 of file scalar_raccord_zec.C.
References etat.
◆ raccord_externe()
| void Lorene::Scalar::raccord_externe | ( | int | puis, |
| int | nbre, | ||
| int | lmax | ||
| ) |
Matching of the external domain with the outermost shell.
Definition at line 69 of file scalar_raccord_externe.C.
References Lorene::Tbl::annule_hard(), Lorene::Valeur::base, Lorene::Valeur::c_cf, Lorene::Valeur::coef(), cos, Lorene::Map_af::get_alpha(), Lorene::Map_af::get_beta(), Lorene::Map::get_mg(), Lorene::Mg3d::get_np(), Lorene::Mg3d::get_nr(), Lorene::Mg3d::get_nt(), Lorene::Mg3d::get_nzone(), Lorene::Tensor::mp, pow, Lorene::Matrice::set(), Lorene::Tbl::set(), Lorene::Mtbl_cf::set(), set_dzpuis(), Lorene::Valeur::set_etat_cf_qcq(), Lorene::Matrice::set_etat_qcq(), Lorene::Mtbl_cf::set_etat_qcq(), Lorene::Tbl::set_etat_qcq(), sqrt, Lorene::Mtbl_cf::t, va, Lorene::Valeur::ylm(), and Lorene::Valeur::ylm_i().
◆ sarra_filter_r()
| void Lorene::Scalar::sarra_filter_r | ( | int | lzmin, |
| int | lzmax, | ||
| double | p, | ||
| double | alpha = -1E-16 |
||
| ) |
Applies an exponential filter to the spectral coefficients in the radial direction.
The filter is of the type: 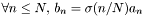 , with
, with 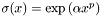 and N the number of radial coefficients.
and N the number of radial coefficients.
- Parameters
-
lzmin,lzmax [input] the indices of the domain where the filter is applied (in [ lzmin,lzmax])p [input] the order of the filter alpha [input] 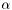 appearing in the above formula.
appearing in the above formula.
Definition at line 108 of file scalar_exp_filter.C.
References etat, Lorene::Map::get_mg(), Lorene::Mg3d::get_nzone(), and Lorene::Tensor::mp.
◆ sarra_filter_r_all_domains()
| void Lorene::Scalar::sarra_filter_r_all_domains | ( | double | p, |
| double | alpha = 1E-16 |
||
| ) |
Applies an exponential filter in radial direction in all domains for the case where p is a double (see Scalar:sarra_filter_r ).
Note that this may cause regularity problems at the origin if applied in a nucleus.
Definition at line 148 of file scalar_exp_filter.C.
References Lorene::Map::get_mg(), Lorene::Tensor::get_mp(), Lorene::Mg3d::get_nzone(), and sarra_filter_r().
◆ sauve()
|
virtual |
Save in a file.
Reimplemented from Lorene::Tensor.
Definition at line 692 of file scalar.C.
References dzpuis, etat, Lorene::fwrite_be(), Lorene::Valeur::sauve(), and va.
◆ scalar_out_bound()
| Scalar Lorene::Scalar::scalar_out_bound | ( | int | n, |
| bool | leave_ylm = false |
||
| ) |
Returns the Scalar containing the values of angular coefficients at the outer boundary.
- Parameters
-
l_dom [input] domain index leave_ylm [input] flag to decide whether the coefficients are expressed in spherical harmonics or Fourier base
Definition at line 479 of file scalar_manip.C.
References Lorene::Valeur::base, Lorene::Valeur::coef(), etat, Lorene::Base_val::get_base_t(), Lorene::Tensor::mp, Lorene::Map::mp_angu(), Lorene::Base_val::set_base_t(), std_spectral_base(), va, and Lorene::Valeur::ylm().
◆ set() [1/4]
Returns the value of a component (read/write version).
- Parameters
-
ind 1-D Itblof sizevalencecontaining the values of each index specifing the component, with the following storage convention:ind(0): value of the first index (1, 2 or 3)ind(1): value of the second index (1, 2 or 3)- and so on...
- Returns
- modifiable reference on the component specified by
ind
Definition at line 664 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), Lorene::Itbl::get_dim(), Lorene::Itbl::get_ndim(), Lorene::Tensor::position(), and Lorene::Tensor::valence.
◆ set() [2/4]
|
inherited |
Returns the value of a component for a tensor of valence 2 (read/write version).
- Parameters
-
i1 value of the first index (1, 2 or 3) i2 value of the second index (1, 2 or 3)
- Returns
- modifiable reference on the component specified by
(i1,i2)
Definition at line 616 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), Lorene::Tensor::position(), Lorene::Itbl::set(), and Lorene::Tensor::valence.
◆ set() [3/4]
|
inherited |
Returns the value of a component for a tensor of valence 3 (read/write version).
- Parameters
-
i1 value of the first index (1, 2 or 3) i2 value of the second index (1, 2 or 3) i3 value of the third index (1, 2 or 3)
- Returns
- modifiable reference on the component specified by
(i1,i2,i3)
Definition at line 631 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), Lorene::Tensor::position(), Lorene::Itbl::set(), and Lorene::Tensor::valence.
◆ set() [4/4]
|
inherited |
Returns the value of a component for a tensor of valence 4 (read/write version).
- Parameters
-
i1 value of the first index (1, 2 or 3) i2 value of the second index (1, 2 or 3) i3 value of the third index (1, 2 or 3) i4 value of the fourth index (1, 2 or 3)
- Returns
- modifiable reference on the component specified by
(i1,i2,i3,i4)
Definition at line 647 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), Lorene::Tensor::position(), Lorene::Itbl::set(), and Lorene::Tensor::valence.
◆ set_dependance()
|
protectedinherited |
To be used to describe the fact that the derivatives members have been calculated with met .
First it sets a null element of met_depend to &met and puts this in the list of the dependancies of met .
Definition at line 463 of file tensor.C.
References Lorene::Tensor::met_depend, and Lorene::Metric::tensor_depend.
◆ set_der_0x0()
|
protected |
◆ set_der_met_0x0()
|
protectedinherited |
Sets all the i-th components of met_depend , p_derive_cov , etc...
to 0x0.
Definition at line 443 of file tensor.C.
References Lorene::Tensor::met_depend, Lorene::Tensor::p_derive_con, Lorene::Tensor::p_derive_cov, and Lorene::Tensor::p_divergence.
◆ set_domain()
|
inline |
Read/write of the value in a given domain.
This method should be used only to set the value in a given domain (it performs a call to del_deriv); for reading the value in a domain without changing it, the method domain(int ) is preferable.
- Parameters
-
l [input] domain index
- Returns
- writable
Tblcontaining the value of the field in domainl.
Definition at line 627 of file scalar.h.
References etat.
◆ set_dzpuis()
| void Lorene::Scalar::set_dzpuis | ( | int | dzi | ) |
Modifies the dzpuis flag.
NB: this method does not change the field values stored in the compactified external domain (use methods dec_dzpuis() , etc... for this purpose).
Definition at line 814 of file scalar.C.
References dzpuis.
◆ set_etat_nondef()
|
virtual |
Sets the logical state to ETATNONDEF (undefined).
Calls the logical destructor of the Valeur va
deallocates the memory occupied by all the derivatives.
Reimplemented from Lorene::Tensor.
Definition at line 350 of file scalar.C.
References etat.
◆ set_etat_one()
| void Lorene::Scalar::set_etat_one | ( | ) |
◆ set_etat_qcq()
|
virtual |
Sets the logical state to ETATQCQ (ordinary state).
If the state is already ETATQCQ , this function does nothing. Otherwise, it calls the logical destructor of the Valeur va and deallocates the memory occupied by all the derivatives.
Reimplemented from Lorene::Tensor.
Definition at line 359 of file scalar.C.
References etat.
◆ set_etat_zero()
|
virtual |
Sets the logical state to ETATZERO (zero).
Calls the logical destructor of the Valeur va and deallocates the memory occupied by all the derivatives.
Reimplemented from Lorene::Tensor.
Definition at line 330 of file scalar.C.
References etat.
◆ set_grid_point()
|
inline |
Setting the value of the field at a given grid point.
CAUTION: to gain in efficiency (especially when this method is invoqued inside a loop), the method del_deriv() (to delete the derived members) is not called by set_grid_point . It must thus be invoqued by the user, after all the calls to set_grid_point have been performed.
- Parameters
-
l [input] domain index k [input]  index
index j [input]  index
index i [input] r (  ) index
) index
- Returns
- writable value of the field at the specified grid point
Definition at line 696 of file scalar.h.
References etat.
◆ set_index_type() [1/2]
|
inlineinherited |
Sets the type of the index number i .
i must be strictly lower than valence and obey the following convention:
i= 0 : first indexi= 1 : second index- and so on...
- Returns
- reference on the type that can be modified (
COVfor a covariant index,CONfor a contravariant one)
Definition at line 950 of file tensor.h.
References Lorene::Itbl::set(), and Lorene::Tensor::type_indice.
◆ set_index_type() [2/2]
|
inlineinherited |
Sets the types of all the indices.
- Returns
- a reference on the 1-D array of integers (class
Itbl) of sizevalencethat can be modified (COVfor a covariant one andCONfor a contravariant one)
Definition at line 959 of file tensor.h.
References Lorene::Tensor::type_indice.
◆ set_inner_boundary()
| void Lorene::Scalar::set_inner_boundary | ( | int | l, |
| double | x | ||
| ) |
Sets the value of the Scalar at the inner boundary of a given domain.
- Parameters
-
l [input] domain index x [input] (constant) value at the inner boundary of domain no. l
Definition at line 295 of file scalar_manip.C.
References etat.
◆ set_outer_boundary()
| void Lorene::Scalar::set_outer_boundary | ( | int | l, |
| double | x | ||
| ) |
Sets the value of the Scalar at the outer boundary of a given domain.
- Parameters
-
l [input] domain index x [input] (constant) value at the outer boundary of domain no. l
Definition at line 327 of file scalar_manip.C.
References etat.
◆ set_spectral_base()
| void Lorene::Scalar::set_spectral_base | ( | const Base_val & | bi | ) |
Sets the spectral bases of the Valeur va
Definition at line 803 of file scalar.C.
References Lorene::Valeur::set_base(), and va.
◆ set_spectral_va()
|
inline |
◆ set_triad()
|
inherited |
Assigns a new vectorial basis (triad) of decomposition.
NB: this function modifies only the member triad and leave unchanged the components (member cmp ). In order to change them coherently with the new basis, the function change_triad(const Base_vect& ) must be called instead.
Definition at line 529 of file tensor.C.
References Lorene::Tensor::triad.
◆ smooth_decay()
| void Lorene::Scalar::smooth_decay | ( | int | k, |
| int | n | ||
| ) |
Performs a 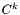 matching of the last non-compactified shell with a decaying function
matching of the last non-compactified shell with a decaying function 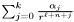 where
where 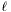 is the spherical harmonic index and n is some specifiable parameter.
is the spherical harmonic index and n is some specifiable parameter.
Definition at line 216 of file scalar_raccord_zec.C.
References etat.
◆ sol_divergence()
| Scalar Lorene::Scalar::sol_divergence | ( | int | n | ) | const |
Resolution of a divergence-like equation.
The equation solved reads: 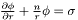 , with
, with  the unknown and
the unknown and  the source represented by
the source represented by this.
- Parameters
-
n [input] the coefficient in front of the 1/r term.
- Returns
- the solution to the equation.
Definition at line 71 of file scalar_sol_div.C.
References etat.
◆ sol_elliptic()
| Scalar Lorene::Scalar::sol_elliptic | ( | Param_elliptic & | params | ) | const |
Resolution of a general elliptic equation, putting zero at infinity.
- Parameters
-
params [input] the operators and variables to be used.
Definition at line 223 of file scalar_pde.C.
References Lorene::Tensor::mp, set_etat_qcq(), and Lorene::Map_af::sol_elliptic().
◆ sol_elliptic_2d()
| Scalar Lorene::Scalar::sol_elliptic_2d | ( | Param_elliptic & | ope_var | ) | const |
Solves the scalar 2-dimensional elliptic equation with *this as a source.
Note that dzpuis must be equal to 2, 3 or 4, i.e. The solution u with the boundary condition u =0 at spatial infinity is the returned Scalar.
Definition at line 398 of file scalar_pde.C.
References Lorene::Tensor::mp, set_etat_qcq(), and Lorene::Map_af::sol_elliptic_2d().
◆ sol_elliptic_boundary() [1/2]
| Scalar Lorene::Scalar::sol_elliptic_boundary | ( | Param_elliptic & | params, |
| const Mtbl_cf & | bound, | ||
| double | fact_dir, | ||
| double | fact_neu | ||
| ) | const |
Resolution of a general elliptic equation, putting zero at infinity and with inner boundary conditions.
- Parameters
-
params [input] the operators and variables to be used. bound [input] : the boundary condition fact_dir : 1 Dirchlet condition, 0 Neumann condition fact_neu : 0 Dirchlet condition, 1 Neumann condition
Definition at line 245 of file scalar_pde.C.
References Lorene::Tensor::mp, set_etat_qcq(), and Lorene::Map_af::sol_elliptic_boundary().
◆ sol_elliptic_boundary() [2/2]
| Scalar Lorene::Scalar::sol_elliptic_boundary | ( | Param_elliptic & | params, |
| const Scalar & | bound, | ||
| double | fact_dir, | ||
| double | fact_neu | ||
| ) | const |
Resolution of general elliptic equation, with inner boundary conditions as Scalars on mono-domain angulare grids.
Definition at line 271 of file scalar_pde.C.
References Lorene::Tensor::mp, set_etat_qcq(), and Lorene::Map_af::sol_elliptic_boundary().
◆ sol_elliptic_fixe_der_zero()
| Scalar Lorene::Scalar::sol_elliptic_fixe_der_zero | ( | double | val, |
| Param_elliptic & | params | ||
| ) | const |
Resolution of a general elliptic equation fixing the dericative at the origin and relaxing one continuity condition.
- Parameters
-
val [input] value of the derivative. params [input] the operators and variables to be used.
Definition at line 375 of file scalar_pde.C.
References Lorene::Tensor::mp, set_etat_qcq(), and Lorene::Map_af::sol_elliptic_fixe_der_zero().
◆ sol_elliptic_no_zec()
| Scalar Lorene::Scalar::sol_elliptic_no_zec | ( | Param_elliptic & | params, |
| double | val = 0 |
||
| ) | const |
Resolution of a general elliptic equation, putting a given value at the outermost shell and not solving in the compactified domain.
- Parameters
-
params [input] the operators and variables to be used. val [input] value at the last shell.
Definition at line 303 of file scalar_pde.C.
References Lorene::Tensor::mp, set_etat_qcq(), and Lorene::Map_af::sol_elliptic_no_zec().
◆ sol_elliptic_only_zec()
| Scalar Lorene::Scalar::sol_elliptic_only_zec | ( | Param_elliptic & | params, |
| double | val | ||
| ) | const |
Resolution of a general elliptic equation solving in the compactified domain and putting a given value at the inner boundary.
- Parameters
-
params [input] the operators and variables to be used. val [input] value at the inner boundary of the external domain.
Definition at line 330 of file scalar_pde.C.
References Lorene::Tensor::mp, set_etat_qcq(), and Lorene::Map_af::sol_elliptic_only_zec().
◆ sol_elliptic_pseudo_1d()
| Scalar Lorene::Scalar::sol_elliptic_pseudo_1d | ( | Param_elliptic & | ope_var | ) | const |
Solves a pseudo-1d elliptic equation with *this as a source.
Definition at line 419 of file scalar_pde.C.
References Lorene::Tensor::mp, set_etat_qcq(), and Lorene::Map_af::sol_elliptic_pseudo_1d().
◆ sol_elliptic_sin_zec()
| Scalar Lorene::Scalar::sol_elliptic_sin_zec | ( | Param_elliptic & | params, |
| double * | coefs, | ||
| double * | phases | ||
| ) | const |
General elliptic solver.
The equation is not solved in the compactified domain and the matching is done with an homogeneous solution.
- Parameters
-
params [input] the operators and variables to be used. coef [output] : coefficient of the oscillatory solution in the external domain. phases [output] : phases (i.e. choice of the homogeneous solution to match with).
Definition at line 352 of file scalar_pde.C.
References Lorene::Tensor::mp, set_etat_qcq(), and Lorene::Map_af::sol_elliptic_sin_zec().
◆ spectral_display()
|
virtual |
Displays the spectral coefficients and the associated basis functions.
This function shows only the values greater than a given threshold.
- Parameters
-
comment comment to be printed at top of the display (default: 0x0 = nothing printed) threshold [input] Value above which a coefficient is printed (default: 1.e-7) precision [input] Number of printed digits (default: 4) ostr [input] Output stream used for the printing (default: cout)
Reimplemented from Lorene::Tensor.
Definition at line 747 of file scalar.C.
References etat.
◆ srdsdt()
| const Scalar & Lorene::Scalar::srdsdt | ( | ) | const |
Returns 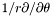 of
of *this .
If dzpuis is zero, then the returned Scalar has dzpuis = 2. It is increased by 1 otherwise.
Definition at line 144 of file scalar_deriv.C.
References etat.
◆ srstdsdp()
| const Scalar & Lorene::Scalar::srstdsdp | ( | ) | const |
Returns 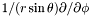 of
of *this .
If dzpuis is zero, then the returned Scalar has dzpuis = 2. It is increased by 1 otherwise.
Definition at line 176 of file scalar_deriv.C.
References etat.
◆ std_spectral_base()
|
virtual |
Sets the spectral bases of the Valeur va to the standard ones for a scalar field.
Reimplemented from Lorene::Tensor.
Definition at line 790 of file scalar.C.
References Lorene::Valeur::std_base_scal(), and va.
◆ std_spectral_base_odd()
|
virtual |
Sets the spectral bases of the Valeur va to the standard odd ones for a scalar field.
Reimplemented from Lorene::Tensor.
Definition at line 797 of file scalar.C.
References Lorene::Valeur::std_base_scal_odd(), and va.
◆ stdsdp()
| const Scalar & Lorene::Scalar::stdsdp | ( | ) | const |
◆ tbl_in_bound()
| Tbl Lorene::Scalar::tbl_in_bound | ( | int | n, |
| bool | leave_ylm = false |
||
| ) |
Returns the Tbl containing the values of angular coefficients at the inner boundary.
- Parameters
-
l_dom [input] domain index leave_ylm [input] flag to decide whether the coefficients are expressed in spherical harmonics or Fourier base
Definition at line 460 of file scalar_manip.C.
References Lorene::Map::get_mg(), Lorene::Mg3d::get_type_r(), and Lorene::Tensor::mp.
◆ tbl_out_bound()
| Tbl Lorene::Scalar::tbl_out_bound | ( | int | l_dom, |
| bool | leave_ylm = false |
||
| ) |
Returns the Tbl containing the values of angular coefficients at the outer boundary.
- Parameters
-
l_dom [input] domain index leave_ylm [input] flag to decide whether the coefficients are expressed in spherical harmonics or Fourier base
Definition at line 442 of file scalar_manip.C.
References Lorene::Valeur::coef(), etat, Lorene::Map::get_mg(), Lorene::Mg3d::get_np(), Lorene::Mg3d::get_nt(), Lorene::Tensor::mp, va, and Lorene::Valeur::ylm().
◆ test_poisson()
Checks if a Poisson equation with *this as a source has been correctly solved.
- Parameters
-
uu [input] Solution u of the Poisson equation 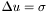 ,
,  being represented by the
being represented by the Scalar*this.ostr [input/output] Output stream used for displaying err.detail [input] - if
truedisplayserr(0,*),err(1,*)anderr(2,*) - if
false(default), displays only the relative errorerr(0,*).
- if
- Returns
- 2-D
Tblerrdecribing the errors in each domain:err(0,l): Relative error in domain no.l, defined as the maximum value of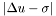 in that domain divided by M , where M is the maximum value of
in that domain divided by M , where M is the maximum value of 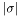 over all domains if
over all domains if dzpuis= 0 or is zero in the compactified external domain (CED). If
is zero in the compactified external domain (CED). If dzpuis!= 0 and does not vanish in the CED, the value of M used in the non-compactified domains is the maximum value over these domains, whereas the value of M used in the compactified external domain is the maximum value on that particular domain.
does not vanish in the CED, the value of M used in the non-compactified domains is the maximum value over these domains, whereas the value of M used in the compactified external domain is the maximum value on that particular domain. err(1,l): Maximum value of the absolute error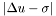 in domain no.
in domain no. l
err(2,l): Maximum value of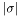 in domain no.
in domain no. l
Definition at line 66 of file scalar_test_poisson.C.
References abs, check_dzpuis(), dzpuis, Lorene::Map::get_mg(), Lorene::Tensor::get_mp(), Lorene::Mg3d::get_nzone(), laplacian(), max, Lorene::Tensor::mp, Lorene::Tbl::set(), and Lorene::Tbl::set_etat_qcq().
◆ trace() [1/4]
|
inherited |
Trace on two different type indices.
- Parameters
-
ind1 first index for the contraction, with the following convention : ind1= 0 : first index of the tensorind1= 1 : second index of the tensor- and so on...
ind2 second index for the contraction
Definition at line 97 of file tensor_calculus.C.
References Lorene::Tensor::cmp, Lorene::Tensor::get_n_comp(), Lorene::Tensor::indices(), Lorene::Tensor::mp, Lorene::Tensor::position(), Lorene::Itbl::set(), Lorene::Tensor::set(), set_etat_zero(), Lorene::Tensor::triad, Lorene::Tensor::type_indice, and Lorene::Tensor::valence.
◆ trace() [2/4]
Trace with respect to a given metric.
- Parameters
-
ind1 first index for the contraction, with the following convention : ind1= 0 : first index of the tensorind1= 1 : second index of the tensor- and so on...
ind2 second index for the contraction gam metric used to raise or lower ind1 in order that it has a opposite type than ind2
Definition at line 156 of file tensor_calculus.C.
References Lorene::Metric::con(), Lorene::contract(), Lorene::Metric::cov(), Lorene::Tensor::trace(), Lorene::Tensor::type_indice, and Lorene::Tensor::valence.
◆ trace() [3/4]
|
inherited |
Trace on two different type indices for a valence 2 tensor.
Definition at line 183 of file tensor_calculus.C.
References Lorene::Tensor::mp, Lorene::Tensor::operator()(), set_etat_zero(), Lorene::Tensor::type_indice, and Lorene::Tensor::valence.
◆ trace() [4/4]
Trace with respect to a given metric for a valence 2 tensor.
- Parameters
-
gam metric used to raise or lower one of the indices, in order to take the trace
Definition at line 200 of file tensor_calculus.C.
References Lorene::Metric::con(), Lorene::contract(), Lorene::Metric::cov(), Lorene::Tensor::trace(), Lorene::Tensor::type_indice, and Lorene::Tensor::valence.
◆ up()
Computes a new tensor by raising an index of *this.
- Parameters
-
ind index to be raised, with the following convention : ind1= 0 : first index of the tensorind1= 1 : second index of the tensor- and so on... (
indmust be of covariant type (COV)).
gam metric used to raise the index (contraction with the twice contravariant form of the metric on the index ind).
Definition at line 228 of file tensor_calculus.C.
References Lorene::Metric::con(), Lorene::contract(), Lorene::Tensor::indices(), Lorene::Tensor::mp, Lorene::Tensor::n_comp, Lorene::Itbl::set(), Lorene::Tensor::set(), Lorene::Tensor::triad, Lorene::Tensor::type_indice, and Lorene::Tensor::valence.
◆ up_down()
Computes a new tensor by raising or lowering all the indices of *this .
- Parameters
-
gam metric used to lower the contravariant indices and raising the covariant ones.
Definition at line 308 of file tensor_calculus.C.
References Lorene::Tensor::down(), Lorene::Tensor::Tensor(), Lorene::Tensor::type_indice, Lorene::Tensor::up(), and Lorene::Tensor::valence.
◆ val_grid_point()
|
inline |
◆ val_point()
| double Lorene::Scalar::val_point | ( | double | r, |
| double | theta, | ||
| double | phi | ||
| ) | const |
Computes the value of the field at an arbitrary point 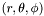 , by means of the spectral expansion.
, by means of the spectral expansion.
NB: if 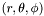 is a point of the spectral grid, the method
is a point of the spectral grid, the method val_grid_point is to be preferred, being much more efficient.
- Parameters
-
r [input] value of the coordinate r theta [input] value of the coordinate 
phi [input] value of the coordinate 
- Returns
- value at the point
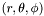 of the field represented by
of the field represented by *this. NB: in the compactified external domain, the returned value is the actual value of the field, i.e. the stored value divided by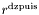 .
.
Definition at line 896 of file scalar.C.
References etat.
◆ visu_box()
| void Lorene::Scalar::visu_box | ( | double | xmin, |
| double | xmax, | ||
| double | ymin, | ||
| double | ymax, | ||
| double | zmin, | ||
| double | zmax, | ||
| const char * | title0 = 0x0, |
||
| const char * | filename0 = 0x0, |
||
| bool | start_dx = true, |
||
| int | nx = 40, |
||
| int | ny = 40, |
||
| int | nz = 40 |
||
| ) | const |
3D visualization (volume rendering) via OpenDX.
Prepares files for visualization by OpenDX of the values of the field in some rectangular box.
- Parameters
-
xmin [input] defines with xmaxthe x range of the visualization boxxmax [input] defines with xminthe x range of the visualization boxymin [input] defines with ymaxthe y range of the visualization boxymax [input] defines with yminthe y range of the visualization boxzmin [input] defines with zmaxthe z range of the visualization boxzmax [input] defines with zminthe z range of the visualization boxtitle [input] title for the graph (for OpenDX legend) filename [input] name for the file which will be the input for OpenDX; the default 0x0 is transformed into "scalar_box" start_dx [input] determines whether OpenDX must be launched (as a subprocess) to view the field; if set to false, only input files for future usage of OpenDX are creatednx [input] number of points in the x direction (uniform sampling)
ny [input] number of points in the y direction (uniform sampling)
nz [input] number of points in the z direction (uniform sampling)
Definition at line 345 of file scalar_visu.C.
References Lorene::Valeur::c_cf, check_dzpuis(), Lorene::Valeur::coef(), Lorene::Map::convert_absolute(), dec_dzpuis(), dzpuis, Lorene::Tensor::mp, Scalar(), va, Lorene::Map::val_lx(), and Lorene::Mtbl_cf::val_point().
◆ visu_section() [1/2]
| void Lorene::Scalar::visu_section | ( | const char | section_type, |
| double | aa, | ||
| double | umin, | ||
| double | umax, | ||
| double | vmin, | ||
| double | vmax, | ||
| const char * | title = 0x0, |
||
| const char * | filename = 0x0, |
||
| bool | start_dx = true, |
||
| int | nu = 200, |
||
| int | nv = 200 |
||
| ) | const |
3D visualization via a plane section.
Prepares files for visualization by OpenDX of the values of the field in a plane x=const, y=const or z=const
- Parameters
-
section_type [input] defines the type of section : - 'x' for a plane x = a with a = const (parameter
aa) - 'y' for a plane y = a with a = const (parameter
aa) - 'z' for a plane z = a with a = const (parameter
aa)
aa [input] constant a defining the section plane umin [input] defines with umaxthe range of the plane coordinate uumax [input] defines with uminthe range of the plane coordinate uvmin [input] defines with vmaxthe range of the plane coordinate vvmax [input] defines with vminthe range of the plane coordinate vtitle [input] title for the graph (for OpenDX legend) filename [input] name for the file which will be the input for OpenDX; the default 0x0 is transformed into "scalar_section" start_dx [input] determines whether OpenDX must be launched (as a subprocess) to view the field; if set to false, only input files for future usage of OpenDX are creatednu [input] number of points in the u direction (uniform sampling)
nv [input] number of points in the v direction (uniform sampling) - 'x' for a plane x = a with a = const (parameter
Definition at line 81 of file scalar_visu.C.
References Lorene::Tbl::set(), and Lorene::Tbl::set_etat_qcq().
◆ visu_section() [2/2]
| void Lorene::Scalar::visu_section | ( | const Tbl & | plane, |
| double | umin, | ||
| double | umax, | ||
| double | vmin, | ||
| double | vmax, | ||
| const char * | title = 0x0, |
||
| const char * | filename = 0x0, |
||
| bool | start_dx = true, |
||
| int | nu = 200, |
||
| int | nv = 200 |
||
| ) | const |
3D visualization via a plane section.
Prepares files for visualization by OpenDX of the values of the field in any given plane.
- Parameters
-
plane [input] : 2D Tbldefining the section plane:planemust of dimension 3x3 with the following content:plane(0,i): absolute Cartesian coordinates (xa0,ya0,za0) of some point in the plane considered as the origin for the plane coordinates (u,v):plane(0,0)= xa0 ,plane(0,1)= ya0 ,plane(0,2)= za0
plane(1,i): components w.r.t. absolute Cartesian coordinates of the u-coordinate unit vector in the section planeplane(2,i): components w.r.t. absolute Cartesian coordinates of the v-coordinate unit vector in the section plane
umin [input] defines with umaxthe range of the plane coordinate uumax [input] defines with uminthe range of the plane coordinate uvmin [input] defines with vmaxthe range of the plane coordinate vvmax [input] defines with vminthe range of the plane coordinate vtitle [input] title for the graph (for OpenDX legend) filename [input] name for the file which will be the input for OpenDX; the default 0x0 is transformed into "scalar_section" start_dx [input] determines whether OpenDX must be launched (as a subprocess) to view the field; if set to false, only input files for future usage of OpenDX are creatednu [input] number of points in the u direction (uniform sampling)
nv [input] number of points in the v direction (uniform sampling)
Definition at line 159 of file scalar_visu.C.
References Lorene::Valeur::c_cf, Lorene::Valeur::coef(), Lorene::Map::convert_absolute(), Lorene::Tensor::mp, va, Lorene::Map::val_lx(), and Lorene::Mtbl_cf::val_point().
◆ visu_section_anim()
| void Lorene::Scalar::visu_section_anim | ( | const char | section_type, |
| double | aa, | ||
| double | umin, | ||
| double | umax, | ||
| double | vmin, | ||
| double | vmax, | ||
| int | jtime, | ||
| double | ttime, | ||
| int | jgraph = 1, |
||
| const char * | title = 0x0, |
||
| const char * | filename_root = 0x0, |
||
| bool | start_dx = false, |
||
| int | nu = 200, |
||
| int | nv = 200 |
||
| ) | const |
3D visualization via time evolving plane section (animation).
Prepares files for visualization by OpenDX of the values of the field in a plane x=const, y=const or z=const at successive time steps
- Parameters
-
section_type [input] defines the type of section : - 'x' for a plane x = a with a = const (parameter
aa) - 'y' for a plane y = a with a = const (parameter
aa) - 'z' for a plane z = a with a = const (parameter
aa)
aa [input] constant a defining the section plane umin [input] defines with umaxthe range of the plane coordinate uumax [input] defines with uminthe range of the plane coordinate uvmin [input] defines with vmaxthe range of the plane coordinate vvmax [input] defines with vminthe range of the plane coordinate vjtime [input] time step label ttime [input] time t corresponding to jtimejgraph [input] number of time steps between two graphs: the graph will be generated only if jtimeis a multiple ofjgraphtitle [input] title for the graph (for OpenDX legend) filename_root [input] beginning of the names for the files which will be the input for OpenDX (the end of names will be automatically generated from the time steps); the default 0x0 is transformed into "anim" start_dx [input] determines whether OpenDX must be launched (as a subprocess) to view the field; if set to false, only input files for future usage of OpenDX are creatednu [input] number of points in the u direction (uniform sampling)
nv [input] number of points in the v direction (uniform sampling) - 'x' for a plane x = a with a = const (parameter
Definition at line 538 of file scalar_visu.C.
References visu_section().
Friends And Related Function Documentation
◆ abs
Absolute value.
Definition at line 526 of file scalar_math.C.
◆ acos
Arccosine.
Definition at line 202 of file scalar_math.C.
◆ asin
Arcsine.
Definition at line 170 of file scalar_math.C.
◆ atan
Arctangent.
Definition at line 234 of file scalar_math.C.
◆ cos
Cosine.
Definition at line 107 of file scalar_math.C.
◆ diffrel
Relative difference between two Scalar (norme version).
- Returns
- 1-D
Tblof size the number of domains, the elements of which arenorme[a(l)-b(l)]/norme[b(l)] ifb(l)!=0andnorme[a(l)-b(l)] ifb(l)=0, wherea(l)andb(l)denote symbolically the values ofaandb
in domain no.l.
Definition at line 698 of file scalar_math.C.
◆ diffrelmax
Relative difference between two Scalar (max version).
- Returns
- 1-D
Tblof size the number of domains, the elements of which aremax[abs(a(l)-b(l))]/max[abs(b(l))] ifb(l)!=0andmax[abs(a(l)-b(l))] ifb(l)=0, wherea(l)andb(l)denote symbolically the values ofaandb
in domain no.l.
Definition at line 733 of file scalar_math.C.
◆ exp
Exponential.
Definition at line 326 of file scalar_math.C.
◆ Heaviside
Heaviside function.
Definition at line 358 of file scalar_math.C.
◆ log
Neperian logarithm.
Definition at line 388 of file scalar_math.C.
◆ log10
Basis 10 logarithm.
Definition at line 421 of file scalar_math.C.
◆ max
Maximum values of a Scalar in each domain.
- Returns
- 1-D
Tblof size the number of domains, the elements of which are the set of the maximum values in each domain.
Definition at line 614 of file scalar_math.C.
◆ min
Minimum values of a Scalar in each domain.
- Returns
- 1-D
Tblof size the number of domains, the elements of which are the set of the minimum values in each domain.
Definition at line 642 of file scalar_math.C.
◆ norme
Sums of the absolute values of all the values of the Scalar in each domain.
- Returns
- 1-D
Tblof size the number of domains, the elements of which are the set of the sums of the absolute values in each domain.
Definition at line 670 of file scalar_math.C.
◆ operator%
Scalar * Scalar with desaliasing.
Definition at line 460 of file scalar_arithm.C.
◆ operator* [1/3]
Definition at line 426 of file scalar_arithm.C.
◆ operator* [2/3]
Definition at line 530 of file scalar_arithm.C.
◆ operator* [3/3]
double * Scalar
Definition at line 571 of file scalar_arithm.C.
◆ operator+ [1/3]
Definition at line 116 of file scalar_arithm.C.
◆ operator+ [2/3]
Scalar + Mbtl.
Definition at line 166 of file scalar_arithm.C.
◆ operator+ [3/3]
Scalar + double.
Definition at line 210 of file scalar_arithm.C.
◆ operator- [1/4]
- Scalar
Definition at line 93 of file scalar_arithm.C.
◆ operator- [2/4]
Definition at line 273 of file scalar_arithm.C.
◆ operator- [3/4]
Scalar - Mbtl.
Definition at line 323 of file scalar_arithm.C.
◆ operator- [4/4]
Scalar - double.
Definition at line 363 of file scalar_arithm.C.
◆ operator/ [1/5]
Definition at line 640 of file scalar_arithm.C.
◆ operator/ [2/5]
Definition at line 678 of file scalar_arithm.C.
◆ operator/ [3/5]
Definition at line 710 of file scalar_arithm.C.
◆ operator/ [4/5]
Scalar / double.
Definition at line 744 of file scalar_arithm.C.
◆ operator/ [5/5]
double / Scalar
Definition at line 778 of file scalar_arithm.C.
◆ operator<<
|
friend |
◆ operator|
Scalar * Scalar with desaliasing only in r.
Definition at line 494 of file scalar_arithm.C.
◆ pow [1/2]
Power 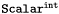 .
.
Definition at line 454 of file scalar_math.C.
◆ pow [2/2]
Power 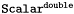 .
.
Definition at line 490 of file scalar_math.C.
◆ racine_cubique
Cube root.
Definition at line 296 of file scalar_math.C.
◆ sin
Sine.
Definition at line 75 of file scalar_math.C.
◆ sqrt
Square root.
Definition at line 266 of file scalar_math.C.
◆ tan
Tangent.
Definition at line 139 of file scalar_math.C.
◆ totalmax
|
friend |
Maximum values of a Scalar in each domain.
- Returns
- 1-D
Tblof size the number of domains, the elements of which are the set of the maximum values in each domain.
Definition at line 556 of file scalar_math.C.
◆ totalmin
|
friend |
Minimum values of a Scalar in each domain.
- Returns
- 1-D
Tblof size the number of domains, the elements of which are the set of the minimum values in each domain.
Definition at line 585 of file scalar_math.C.
Member Data Documentation
◆ cmp
|
protectedinherited |
◆ dzpuis
|
protected |
◆ etat
|
protected |
◆ ind_lap
|
mutableprotected |
◆ met_depend
|
mutableprotectedinherited |
◆ mp
|
protectedinherited |
◆ n_comp
|
protectedinherited |
◆ p_derive_con
|
mutableprotectedinherited |
Array of pointers on the contravariant derivatives of this with respect to various metrics.
See the comments of met_depend . See also the comments of method derive_con() for a precise definition of a "contravariant" derivative.
◆ p_derive_cov
|
mutableprotectedinherited |
Array of pointers on the covariant derivatives of this with respect to various metrics.
See the comments of met_depend . See also the comments of method derive_cov() for the index convention of the covariant derivation.
◆ p_divergence
|
mutableprotectedinherited |
Array of pointers on the divergence of this with respect to various metrics.
See the comments of met_depend . See also the comments of method divergence() for a precise definition of a the divergence with respect to a given metric.
◆ p_dsdr
|
mutableprotected |
◆ p_dsdradial
|
mutableprotected |
◆ p_dsdrho
|
mutableprotected |
◆ p_dsdt
|
mutableprotected |
◆ p_dsdx
|
mutableprotected |
◆ p_dsdy
|
mutableprotected |
◆ p_dsdz
|
mutableprotected |
◆ p_integ
|
mutableprotected |
◆ p_lap
|
mutableprotected |
◆ p_lapang
|
mutableprotected |
◆ p_srdsdt
|
mutableprotected |
◆ p_srstdsdp
|
mutableprotected |
◆ p_stdsdp
|
mutableprotected |
◆ triad
|
protectedinherited |
◆ type_indice
|
protectedinherited |
◆ va
|
protected |
◆ valence
|
protectedinherited |
The documentation for this class was generated from the following files:
- scalar.h
- scalar.C
- scalar_arithm.C
- scalar_asymptot.C
- scalar_deriv.C
- scalar_exp_filter.C
- scalar_import.C
- scalar_import_asymy.C
- scalar_import_symy.C
- scalar_integ.C
- scalar_manip.C
- scalar_match_tau.C
- scalar_pde.C
- scalar_pde_frontiere.C
- scalar_poisson_regu.C
- scalar_r_manip.C
- scalar_raccord.C
- scalar_raccord_externe.C
- scalar_raccord_zec.C
- scalar_sol_div.C
- scalar_test_poisson.C
- scalar_th_manip.C
- scalar_visu.C
