Bases of the spectral expansions. More...
#include <base_val.h>
Public Member Functions | |
| Base_val (int nb_of_domains) | |
| Standard constructor. More... | |
| Base_val (const Base_val &) | |
| Copy constructor. More... | |
| Base_val (FILE *) | |
Constructor from a file (see sauve(FILE*) ) More... | |
| ~Base_val () | |
| Destructor. More... | |
| void | set_base_nondef () |
Sets the spectral bases to NONDEF. More... | |
| void | set_base_r (int l, int base_r) |
Sets the expansion basis for r (  ) functions in a given domain. More... ) functions in a given domain. More... | |
| void | set_base_t (int base_t) |
Sets the expansion basis for  functions in all domains. More... functions in all domains. More... | |
| void | set_base_p (int base_p) |
Sets the expansion basis for  functions in all domains. More... functions in all domains. More... | |
| void | operator= (const Base_val &) |
| Assignment. More... | |
| bool | operator== (const Base_val &) const |
| Comparison operator. More... | |
| int | get_b (int l) const |
Returns the code for the expansion basis in domain no. l. More... | |
| int | get_base_r (int l) const |
Returns the expansion basis for r (  ) functions in the domain of index ) functions in the domain of index l (e.g. More... | |
| int | get_base_t (int l) const |
Returns the expansion basis for  functions in the domain of index functions in the domain of index l (e.g. More... | |
| int | get_base_p (int l) const |
Returns the expansion basis for  functions in the domain of index functions in the domain of index l (e.g. More... | |
| void | name_r (int l, int k, int j, int i, string &basename) const |
Name of the basis function in r (  ) More... ) More... | |
| void | name_theta (int l, int k, int j, string &basename) const |
Name of the basis function in  . More... . More... | |
| void | name_phi (int l, int k, string &basename) const |
Name of the basis function in 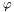 . More... . More... | |
| const Tbl & | theta_functions (int l, int nt) const |
| Values of the theta basis functions at the theta collocation points. More... | |
| const Tbl & | phi_functions (int l, int np) const |
| Values of the phi basis functions at the phi collocation points. More... | |
| int | get_nzone () const |
| Returns the number of domains. More... | |
| void | dsdx () |
The basis is transformed as with a 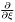 operation. More... operation. More... | |
| void | sx () |
The basis is transformed as with a 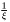 multiplication. More... multiplication. More... | |
| void | mult_x () |
The basis is transformed as with a multiplication by  . More... . More... | |
| void | dsdt () |
The basis is transformed as with a 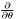 operation. More... operation. More... | |
| void | ssint () |
The basis is transformed as with a 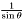 multiplication. More... multiplication. More... | |
| void | mult_sint () |
The basis is transformed as with a 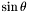 multiplication. More... multiplication. More... | |
| void | mult_cost () |
The basis is transformed as with a 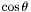 multiplication. More... multiplication. More... | |
| void | ylm () |
The basis is transformed as with a transformation to 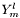 basis. More... basis. More... | |
| void | give_quant_numbers (int, int, int, int &, int &, int &) const |
| Computes the various quantum numbers and 1d radial base. More... | |
| int | give_lmax (const Mg3d &mgrid, int lz) const |
| Returns the highest multipole for a given grid. More... | |
| void | sauve (FILE *) const |
| Save in a file. More... | |
Public Attributes | |
| int * | b |
Array (size: nzone ) of the spectral basis in each domain. More... | |
Protected Attributes | |
| int | nzone |
| Number of domains (zones) More... | |
Friends | |
| ostream & | operator<< (ostream &, const Base_val &) |
| Display. More... | |
| Base_val | operator* (const Base_val &, const Base_val &) |
This operator is used when calling multiplication or division of Valeur . More... | |
Detailed Description
Bases of the spectral expansions.
()
The class Base_val describes, in each domain, on which basis the spectral expansion of a given function is performed. The corresponding coefficients will be stored in a Mtbl_cf.
The various bases in each of the three dimensions r ,  and
and  are identified by an integer defined by a macro in the file
are identified by an integer defined by a macro in the file type_parite.h. These three integers are then merged (by means of the bitwise OR operator) to give a single integer, stored in Base_val::b[l],
l being the domain index. The bases in r ,  and
and  can be restored by applying the bitwise AND operator with the masks
can be restored by applying the bitwise AND operator with the masks MSQ_R, MSQ_T and MSQ_P defined in type_parite.h.
The basis functions for expansion with respect to the radial coordinate  are coded as follows, m being the order of the Fourier expansion in
are coded as follows, m being the order of the Fourier expansion in  :
:
R_CHEB(0x00000001) : Chebyshev polynomials (r -sampling:FIN);R_CHEBP(0x00000002) : Even Chebyshev polynomials (r -sampling:RARE);R_CHEBI(0x00000003) : Odd Chebyshev polynomials (r -sampling:RARE);R_CHEBPI_P(0x00000004) : Even (resp. odd) Chebyshev polynomials for l (spherical harmonic index) even (resp. odd) (r -sampling:RARE);R_CHEBPI_I(0x00000005) : Odd (resp. even) Chebyshev polynomials for l (spherical harmonic index) even (resp. odd) (r -sampling:RARE) ;R_CHEBPIM_P(0x00000006) : Even (resp. odd) Chebyshev polynomials for m even (resp. odd) (r -sampling:RARE);R_CHEBPIM_I(0x00000007) : Odd (resp. even) Chebyshev polynomials for m even (resp. odd) (r -sampling:RARE) ;R_CHEBU(0x00000008) : Chebyshev polynomials (r -sampling:UNSURR) ;R_LEG(0x00000009) : Legendre polynomials (r -sampling:FIN);R_LEGP(0x0000000a) : Even Legendre polynomials (r -sampling:RARE);R_LEGI(0x0000000b) : Odd Legendre polynomials (r -sampling:RARE);R_JACO02(0x0000000c) : Jacobi(0,2) polynomials (r -sampling:FIN).
The basis functions for expansion with respect to the co-latitude coordinate  are coded as follows, m being the order of the Fourier expansion in
are coded as follows, m being the order of the Fourier expansion in  :
:
T_COSSIN_C(0x00000100) :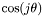 for m even,
for m even, 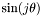 for m odd (
for m odd (  -sampling:
-sampling: NONSYM);T_COSSIN_S(0x00000200) :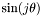 for m even,
for m even, 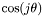 for m odd (
for m odd (  -sampling:
-sampling: NONSYM);T_COS(0x00000300) :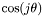 m being always even and (
m being always even and (  -sampling:
-sampling: NONSYM);T_SIN(0x00000400) :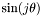 m being always even, (
m being always even, (  -sampling:
-sampling: NONSYM);T_COS_P(0x00000500) :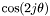 (
(  -sampling:
-sampling: SYM);T_SIN_P(0x00000600) :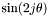 (
(  -sampling:
-sampling: SYM);T_COS_I(0x00000700) :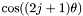 (
(  -sampling:
-sampling: SYM);T_SIN_I(0x00000800) :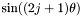 (
(  -sampling:
-sampling: SYM);T_COSSIN_CP(0x00000900) :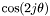 for m even,
for m even, 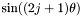 for m odd (
for m odd (  -sampling:
-sampling: SYM);T_COSSIN_SP(0x00000a00) :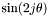 for m even,
for m even, 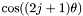 for m odd (
for m odd (  -sampling:
-sampling: SYM);T_COSSIN_CI(0x00000b00) :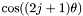 for m even,
for m even, 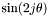 for m odd (
for m odd (  -sampling:
-sampling: SYM);T_COSSIN_SI(0x00000c00) :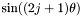 for m even,
for m even, 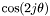 for m odd (
for m odd (  -sampling:
-sampling: SYM);T_LEG_P(0x00000d00) : Associated Legendre functions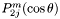 for m even,
for m even, 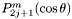 for m odd (
for m odd (  -sampling:
-sampling: SYM);T_LEG_PP(0x00000e00) : Associated Legendre functions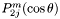 , m being always even (
, m being always even (  -sampling:
-sampling: SYM);T_LEG_I(0x00000f00) : Associated Legendre functions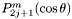 for m even,
for m even, 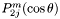 for m odd (
for m odd (  -sampling:
-sampling: SYM);T_LEG_IP(0x00001000) : Associated Legendre functions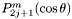 , m being always even (
, m being always even (  -sampling:
-sampling: SYM);T_LEG_PI(0x00001100) : Associated Legendre functions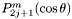 , m being always odd (
, m being always odd (  -sampling:
-sampling: SYM);T_LEG_II(0x00001200) : Associated Legendre functions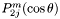 , m being always odd (
, m being always odd (  -sampling:
-sampling: SYM);T_LEG(0x00001700) : Associated Legendre functions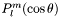 of all types ;
of all types ; T_LEG_MP(0x00001800) : Associated Legendre functions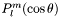 m being always even (
m being always even (  -sampling:
-sampling: NONSYM);T_LEG_MI(0x00001900) : Associated Legendre functions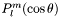 m being always odd (
m being always odd (  -sampling:
-sampling: NONSYM);
The basis functions for expansion with respect to the azimuthal coordinate  are coded as follows
are coded as follows
P_COSSIN(0x00010000) : Fourrier series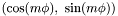 (
(  -sampling:
-sampling: NONSYM);P_COSSIN_P(0x00020000) : Fourrier series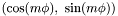 with even harmonics only (i.e. m even) (
with even harmonics only (i.e. m even) (  -sampling:
-sampling: SYM);P_COSSIN_I(0x00030000) : Fourrier series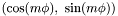 with odd harmonics only (i.e. m odd) (
with odd harmonics only (i.e. m odd) (  -sampling:
-sampling: SYM);
Definition at line 325 of file base_val.h.
Constructor & Destructor Documentation
◆ Base_val() [1/3]
|
explicit |
◆ Base_val() [2/3]
| Lorene::Base_val::Base_val | ( | const Base_val & | bi | ) |
◆ Base_val() [3/3]
|
explicit |
Constructor from a file (see sauve(FILE*) )
Definition at line 169 of file base_val.C.
References b, Lorene::fread_be(), and nzone.
◆ ~Base_val()
| Lorene::Base_val::~Base_val | ( | ) |
Member Function Documentation
◆ dsdt()
| void Lorene::Base_val::dsdt | ( | ) |
The basis is transformed as with a 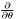 operation.
operation.
Definition at line 193 of file base_val_manip.C.
References get_base_t(), set_base_t(), T_COS, T_COS_I, T_COS_P, T_COSSIN_C, T_COSSIN_CI, T_COSSIN_CP, T_COSSIN_S, T_COSSIN_SI, T_COSSIN_SP, T_SIN, T_SIN_I, and T_SIN_P.
◆ dsdx()
| void Lorene::Base_val::dsdx | ( | ) |
The basis is transformed as with a 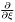 operation.
operation.
Definition at line 94 of file base_val_manip.C.
References get_base_r(), R_CHEBI, R_CHEBP, R_CHEBPI_I, R_CHEBPI_P, R_CHEBPIM_I, R_CHEBPIM_P, R_LEGI, R_LEGP, and set_base_r().
◆ get_b()
|
inline |
Returns the code for the expansion basis in domain no. l.
Definition at line 392 of file base_val.h.
◆ get_base_p()
|
inline |
◆ get_base_r()
|
inline |
◆ get_base_t()
|
inline |
◆ get_nzone()
|
inline |
◆ give_lmax()
| int Lorene::Base_val::give_lmax | ( | const Mg3d & | mgrid, |
| int | lz | ||
| ) | const |
Returns the highest multipole for a given grid.
- Parameters
-
mgrid : the Mg3dlz : the domain to consider
- Returns
- the highest multipolar momentum l that can be described by
thisbase on the grid.
Definition at line 297 of file base_val_quantum.C.
References get_base_t(), Lorene::Mg3d::get_np(), Lorene::Mg3d::get_nt(), Lorene::Mg3d::get_nzone(), T_CL_COS_I, T_CL_COS_P, T_CL_SIN_I, T_CL_SIN_P, T_COS, T_COS_I, T_COS_P, T_COSSIN_C, T_COSSIN_CI, T_COSSIN_CP, T_COSSIN_S, T_COSSIN_SI, T_COSSIN_SP, T_LEG, T_LEG_I, T_LEG_II, T_LEG_IP, T_LEG_MI, T_LEG_MP, T_LEG_P, T_LEG_PI, T_LEG_PP, T_SIN_I, and T_SIN_P.
◆ give_quant_numbers()
| void Lorene::Base_val::give_quant_numbers | ( | int | l, |
| int | k, | ||
| int | j, | ||
| int & | m_quant, | ||
| int & | l_quant, | ||
| int & | base_r_1d | ||
| ) | const |
Computes the various quantum numbers and 1d radial base.
Definition at line 84 of file base_val_quantum.C.
References get_base_p(), get_base_r(), get_base_t(), P_COSSIN, P_COSSIN_I, P_COSSIN_P, R_CHEB, R_CHEBI, R_CHEBP, R_CHEBPI_I, R_CHEBPI_P, R_CHEBPIM_I, R_CHEBPIM_P, R_CHEBU, R_JACO02, R_LEG, R_LEGI, R_LEGP, T_CL_COS_I, T_CL_COS_P, T_CL_SIN_I, T_CL_SIN_P, T_COS, T_COS_I, T_COS_P, T_COSSIN_C, T_COSSIN_CI, T_COSSIN_CP, T_COSSIN_S, T_COSSIN_SI, T_COSSIN_SP, T_LEG, T_LEG_I, T_LEG_II, T_LEG_IP, T_LEG_MI, T_LEG_MP, T_LEG_P, T_LEG_PI, T_LEG_PP, T_SIN_I, and T_SIN_P.
◆ mult_cost()
| void Lorene::Base_val::mult_cost | ( | ) |
The basis is transformed as with a 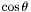 multiplication.
multiplication.
Definition at line 337 of file base_val_manip.C.
References get_base_t(), set_base_t(), T_COS, T_COS_I, T_COS_P, T_COSSIN_C, T_COSSIN_CI, T_COSSIN_CP, T_COSSIN_S, T_COSSIN_SI, T_COSSIN_SP, T_SIN, T_SIN_I, and T_SIN_P.
◆ mult_sint()
| void Lorene::Base_val::mult_sint | ( | ) |
The basis is transformed as with a 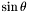 multiplication.
multiplication.
Definition at line 289 of file base_val_manip.C.
References get_base_t(), set_base_t(), T_COS, T_COS_I, T_COS_P, T_COSSIN_C, T_COSSIN_CI, T_COSSIN_CP, T_COSSIN_S, T_COSSIN_SI, T_COSSIN_SP, T_SIN, T_SIN_I, and T_SIN_P.
◆ mult_x()
| void Lorene::Base_val::mult_x | ( | ) |
The basis is transformed as with a multiplication by  .
.
Definition at line 160 of file base_val_manip.C.
References get_base_r(), R_CHEBI, R_CHEBP, R_CHEBPI_I, R_CHEBPI_P, R_CHEBPIM_I, R_CHEBPIM_P, R_LEGI, R_LEGP, and set_base_r().
◆ name_phi()
| void Lorene::Base_val::name_phi | ( | int | l, |
| int | k, | ||
| string & | basename | ||
| ) | const |
Name of the basis function in 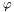 .
.
- Parameters
-
l [input] domain index k [input] phi index basename [output] string containing the name of the basis function;
Definition at line 78 of file base_val_name_phi.C.
References b, MAX_BASE_2, MSQ_P, nzone, P_COSSIN, P_COSSIN_I, P_COSSIN_P, and TRA_P.
◆ name_r()
| void Lorene::Base_val::name_r | ( | int | l, |
| int | k, | ||
| int | j, | ||
| int | i, | ||
| string & | basename | ||
| ) | const |
Name of the basis function in r (  )
)
- Parameters
-
l [input] domain index k [input] phi index (for the basis in r may depend upon the phi index) j [input] theta index (for the basis in r may depend upon the theta index) i [input] r index basename [output] string containing the name of the basis function;
Definition at line 93 of file base_val_name_r.C.
References b, MAX_BASE, MSQ_R, nzone, R_CHEB, R_CHEBI, R_CHEBP, R_CHEBPI_I, R_CHEBPI_P, R_CHEBPIM_I, R_CHEBPIM_P, R_CHEBU, R_JACO02, R_LEG, R_LEGI, R_LEGP, and TRA_R.
◆ name_theta()
| void Lorene::Base_val::name_theta | ( | int | l, |
| int | k, | ||
| int | j, | ||
| string & | basename | ||
| ) | const |
Name of the basis function in  .
.
- Parameters
-
l [input] domain index k [input] phi index (for the basis in  may depend upon the phi index)
may depend upon the phi index) j [input] theta index basename [output] string containing the name of the basis function;
Definition at line 123 of file base_val_name_theta.C.
References b, MAX_BASE, MSQ_T, nzone, T_CL_COS_I, T_CL_COS_P, T_CL_SIN_I, T_CL_SIN_P, T_COS, T_COS_I, T_COS_P, T_COSSIN_C, T_COSSIN_CI, T_COSSIN_CP, T_COSSIN_S, T_COSSIN_SI, T_COSSIN_SP, T_LEG, T_LEG_I, T_LEG_II, T_LEG_IP, T_LEG_MI, T_LEG_MP, T_LEG_P, T_LEG_PI, T_LEG_PP, T_SIN, T_SIN_I, T_SIN_P, and TRA_T.
◆ operator=()
| void Lorene::Base_val::operator= | ( | const Base_val & | bi | ) |
◆ operator==()
| bool Lorene::Base_val::operator== | ( | const Base_val & | c2 | ) | const |
◆ phi_functions()
| const Tbl & Lorene::Base_val::phi_functions | ( | int | l, |
| int | np | ||
| ) | const |
Values of the phi basis functions at the phi collocation points.
- Parameters
-
l [input] domain index np [input] number of phi collocation points (or equivalently number of phi basis functions) in the domain of index l
- Returns
- resu :
Tbl2-D containing the values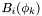 of the
of the npphi basis functions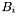 at the
at the np
collocation points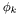 in the domain of index
in the domain of index l. The storage convention is the following one : \resu(i,k)=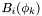 .
.
Definition at line 91 of file base_val_phi_funct.C.
References b, MAX_BASE_2, MSQ_P, P_COSSIN, P_COSSIN_I, P_COSSIN_P, and TRA_P.
◆ sauve()
| void Lorene::Base_val::sauve | ( | FILE * | fd | ) | const |
Save in a file.
Definition at line 231 of file base_val.C.
References b, Lorene::fwrite_be(), and nzone.
◆ set_base_nondef()
| void Lorene::Base_val::set_base_nondef | ( | ) |
Sets the spectral bases to NONDEF.
Definition at line 329 of file base_val.C.
◆ set_base_p()
| void Lorene::Base_val::set_base_p | ( | int | base_p | ) |
◆ set_base_r()
| void Lorene::Base_val::set_base_r | ( | int | l, |
| int | base_r | ||
| ) |
Sets the expansion basis for r (  ) functions in a given domain.
) functions in a given domain.
- Parameters
-
l Domain index base_r type of basis functions in r (  ) (e.g.
) (e.g. R_CHEB_P, etc..., see general documentation of classBase_valfor denomination of the various bases).
Definition at line 188 of file base_val.C.
◆ set_base_t()
| void Lorene::Base_val::set_base_t | ( | int | base_t | ) |
◆ ssint()
| void Lorene::Base_val::ssint | ( | ) |
The basis is transformed as with a 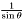 multiplication.
multiplication.
Definition at line 241 of file base_val_manip.C.
References get_base_t(), set_base_t(), T_COS, T_COS_I, T_COS_P, T_COSSIN_C, T_COSSIN_CI, T_COSSIN_CP, T_COSSIN_S, T_COSSIN_SI, T_COSSIN_SP, T_SIN, T_SIN_I, and T_SIN_P.
◆ sx()
| void Lorene::Base_val::sx | ( | ) |
The basis is transformed as with a 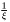 multiplication.
multiplication.
Definition at line 127 of file base_val_manip.C.
References get_base_r(), R_CHEBI, R_CHEBP, R_CHEBPI_I, R_CHEBPI_P, R_CHEBPIM_I, R_CHEBPIM_P, R_LEGI, R_LEGP, and set_base_r().
◆ theta_functions()
| const Tbl & Lorene::Base_val::theta_functions | ( | int | l, |
| int | nt | ||
| ) | const |
Values of the theta basis functions at the theta collocation points.
- Parameters
-
l [input] domain index nt [input] number of theta collocation points (or equivalently number of theta basis functions) in the domain of index l
- Returns
- resu :
Tbl3-D containing the values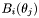 of the
of the nttheta basis functions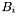 at the
at the ntcollocation points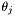 in the domain of index
in the domain of index l. The storage convention is the following one : \resu(ind_phi,i,j)=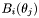 with
with ind_phibeing a supplementary dimension in case of a dependence in phi of the theta basis : for example, if the theta basis isT_COS_P(no dependence in phi),resu.get_dim(2)= 1 andind_phican take only the value 0; if the theta basis isT_COSSIN_CP,resu.get_dim(2)= 2, withind_phi= 0 for m even and
ind_phi= 1 for m odd.
Definition at line 112 of file base_val_theta_funct.C.
References b, MAX_BASE, MSQ_T, T_COS, T_COS_I, T_COS_P, T_COSSIN_C, T_COSSIN_CI, T_COSSIN_CP, T_COSSIN_S, T_COSSIN_SI, T_COSSIN_SP, T_SIN, T_SIN_I, T_SIN_P, and TRA_T.
◆ ylm()
| void Lorene::Base_val::ylm | ( | ) |
The basis is transformed as with a transformation to 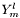 basis.
basis.
Definition at line 385 of file base_val_manip.C.
References get_base_t(), set_base_t(), T_COS, T_COS_I, T_COS_P, T_COSSIN_C, T_COSSIN_CI, T_COSSIN_CP, T_COSSIN_S, T_LEG, T_LEG_I, T_LEG_II, T_LEG_IP, T_LEG_MP, T_LEG_P, T_LEG_PI, T_LEG_PP, T_SIN_I, and T_SIN_P.
Friends And Related Function Documentation
◆ operator*
This operator is used when calling multiplication or division of Valeur .
It returns the appropriate base, taking into account the symmetry of the result. The calculation propreties are those of the multiplication of -1 for antisymmetry and 1 for symmetry.
Should the product of the Base_val not be possible, the result is set to ETATNONDEF , (state not defined). It would be the case, for example, if one and only one of the Valeur is given in spherical harmonics.
Definition at line 105 of file base_val_mult.C.
◆ operator<<
|
friend |
Display.
Definition at line 241 of file base_val.C.
Member Data Documentation
◆ b
| int* Lorene::Base_val::b |
Array (size: nzone ) of the spectral basis in each domain.
Definition at line 334 of file base_val.h.
◆ nzone
|
protected |
Number of domains (zones)
Definition at line 330 of file base_val.h.
The documentation for this class was generated from the following files:
