Component of a tensorial field *** DEPRECATED : use class Scalar instead ***.
More...
#include <cmp.h>
Public Member Functions | |
| Cmp (const Map &map) | |
| Constructor from mapping. More... | |
| Cmp (const Map *p_map) | |
| Constructor from mapping. More... | |
| Cmp (const Cmp &a) | |
| Copy constructor. More... | |
| Cmp (const Map &, const Mg3d &, FILE *) | |
Constructor from a file (see sauve(FILE*) ) More... | |
| ~Cmp () | |
| Destructor. More... | |
| void | operator= (const Cmp &a) |
Assignment to another Cmp defined on the same mapping. More... | |
| void | operator= (const Valeur &a) |
Assignment to a Valeur. More... | |
| void | operator= (const Mtbl &a) |
Assignment to a Mtbl. More... | |
| void | operator= (double) |
Assignment to a double. More... | |
| void | operator= (int) |
Assignment to an int. More... | |
| void | import (const Cmp &ci) |
Assignment to another Cmp defined on a different mapping. More... | |
| void | import_symy (const Cmp &ci) |
Assignment to another Cmp defined on a different mapping. More... | |
| void | import_asymy (const Cmp &ci) |
Assignment to another Cmp defined on a different mapping. More... | |
| void | import (int nzet, const Cmp &ci) |
Assignment to another Cmp defined on a different mapping. More... | |
| void | import_symy (int nzet, const Cmp &ci) |
Assignment to another Cmp defined on a different mapping. More... | |
| void | import_asymy (int nzet, const Cmp &ci) |
Assignment to another Cmp defined on a different mapping. More... | |
| Tbl & | set (int l) |
| Read/write of the value in a given domain. More... | |
| const Tbl & | operator() (int l) const |
| Read-only of the value in a given domain. More... | |
| double & | set (int l, int k, int j, int i) |
| Read/write of a particular element. More... | |
| double | operator() (int l, int k, int j, int i) const |
| Read-only of a particular element. More... | |
| double | val_point (double r, double theta, double phi) const |
Computes the value of the field represented by *this at an arbitrary point 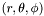 , by means of the spectral expansion. More... , by means of the spectral expansion. More... | |
| void | set_etat_nondef () |
Sets the logical state to ETATNONDEF (undefined). More... | |
| void | set_etat_zero () |
Sets the logical state to ETATZERO (zero). More... | |
| void | set_etat_qcq () |
Sets the logical state to ETATQCQ (ordinary state). More... | |
| void | allocate_all () |
Sets the logical state to ETATQCQ (ordinary state) and performs the memory allocation of all the elements, down to the double arrays of the Tbl s. More... | |
| void | annule_hard () |
Sets the Cmp to zero in a hard way. More... | |
| void | annule (int l) |
Sets the Cmp to zero in a given domain. More... | |
| void | annule (int l_min, int l_max) |
Sets the Cmp to zero in several domains. More... | |
| void | filtre (int n) |
Sets the n lasts coefficients in r to 0 in the external domain. More... | |
| void | filtre_phi (int n, int zone) |
Sets the n lasts coefficients in 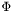 to 0 in the domain to 0 in the domain zone . More... | |
| void | set_val_inf (double val) |
Sets the value of the Cmp to val at infinity. More... | |
| void | set_val_hor (double val, int zone) |
Sets the value of the Cmp to val on the inner boudary of the shell number zone .This is usefull for dealing with undefined values. More... | |
| void | fixe_decroissance (int puis) |
Substracts all the components behaving like 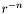 in the external domain, with n strictly lower than in the external domain, with n strictly lower than puis , so that *this decreases at least like 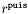 at infinity. More... at infinity. More... | |
| Tbl | multipole_spectrum () |
| Gives the spectrum in terms of multipolar modes l . More... | |
| int | get_etat () const |
| Returns the logical state. More... | |
| const Map * | get_mp () const |
| Returns the mapping. More... | |
| int | get_dzpuis () const |
Returns dzpuis. More... | |
| bool | dz_nonzero () const |
Returns true if the last domain is compactified and *this is not zero in this domain. More... | |
| bool | check_dzpuis (int dzi) const |
Returns false if the last domain is compactified and *this is not zero in this domain and dzpuis is not equal to dzi , otherwise return true. More... | |
| void | sauve (FILE *) const |
| Save in a file. More... | |
| void | affiche_seuil (ostream &ostr, int type=0, int precision=4, double threshold=1.e-7) const |
| Prints only the values greater than a given threshold. More... | |
| void | operator+= (const Cmp &) |
| += Cmp More... | |
| void | operator-= (const Cmp &) |
| -= Cmp More... | |
| void | operator*= (const Cmp &) |
| *= Cmp More... | |
| void | std_base_scal () |
Sets the spectral bases of the Valeur va to the standard ones for a scalar. More... | |
| const Cmp & | dsdr () const |
Returns 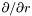 of of *this . More... | |
| const Cmp & | srdsdt () const |
Returns 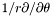 of of *this . More... | |
| const Cmp & | srstdsdp () const |
Returns 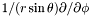 of of *this . More... | |
| const Cmp & | dsdx () const |
Returns 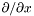 of of *this , where 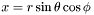 . More... . More... | |
| const Cmp & | dsdy () const |
Returns 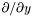 of of *this , where 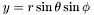 . More... . More... | |
| const Cmp & | dsdz () const |
Returns 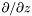 of of *this , where 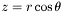 . More... . More... | |
| const Cmp & | deriv (int i) const |
Returns 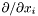 of of *this , where 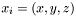 . More... . More... | |
| const Cmp & | laplacien (int zec_mult_r=4) const |
Returns the Laplacian of *this. More... | |
| void | div_r () |
| Division by r everywhere. More... | |
| void | mult_r () |
| Multiplication by r everywhere. More... | |
| void | mult_r_zec () |
| Multiplication by r in the external compactified domain (ZEC) More... | |
| void | mult_rsint () |
Multiplication by 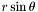 . More... . More... | |
| void | mult_cost () |
| Multiplication by $. More... | |
| Division by f $r sin theta f void | div_rsint () |
| void | dec_dzpuis () |
Decreases by 1 the value of dzpuis and changes accordingly the values of the Cmp in the external compactified domain (ZEC). More... | |
| void | inc_dzpuis () |
Increases by the value of dzpuis and changes accordingly the values of the Cmp in the external compactified domain (ZEC). More... | |
| void | dec2_dzpuis () |
Decreases by 2 the value of dzpuis and changes accordingly the values of the Cmp in the external compactified domain (ZEC). More... | |
| void | inc2_dzpuis () |
Increases by 2 the value of dzpuis and changes accordingly the values of the Cmp in the external compactified domain (ZEC). More... | |
| void | set_dzpuis (int) |
Set a value to dzpuis. More... | |
| double | integrale () const |
Computes the integral over all space of *this . More... | |
| const Tbl & | integrale_domains () const |
Computes the integral in each domain of *this . More... | |
| Valeur ** | asymptot (int n, const int flag=0) const |
| Asymptotic expansion at r = infinity. More... | |
| Cmp | poisson () const |
Solves the scalar Poisson equation with *this as a source. More... | |
| Cmp | poisson_tau () const |
| Same as Poisson with a Tau method. More... | |
| Cmp | poisson_falloff (int k_falloff) const |
| Cmp | poisson_ylm (int nylm, double *intvec) const |
| void | poisson (Param &par, Cmp &uu) const |
Solves the scalar Poisson equation with *this as a source (version with parameters to control the resolution). More... | |
| void | poisson_tau (Param &par, Cmp &uu) const |
| Same as Poisson with a Tau method. More... | |
| void | poisson_falloff (Param &par, Cmp &uu, int k_falloff) const |
| void | poisson_ylm (Param &par, Cmp &uu, int nylm, double *intvec) const |
| Cmp | poisson_dirichlet (const Valeur &limite, int num) const |
Is identicall to Cmp::poisson() . More... | |
| Cmp | poisson_neumann (const Valeur &, int) const |
Idem as Cmp::poisson_dirichlet , the boundary condition being on the radial derivative of the solution. More... | |
| Cmp | poisson_neumann_interne (const Valeur &, Param &par, Cmp &resu) const |
Idem as Cmp::poisson_neumann , the boundary condition is on the radial derivative of the solution. More... | |
| Cmp | poisson_frontiere_double (const Valeur &, const Valeur &, int) const |
| void | poisson_regular (int k_div, int nzet, double unsgam1, Param &par, Cmp &uu, Cmp &uu_regu, Cmp &uu_div, Tenseur &duu_div, Cmp &source_regu, Cmp &source_div) const |
Solves the scalar Poisson equation with *this as a source (version with parameters to control the resolution). More... | |
| Tbl | test_poisson (const Cmp &uu, ostream &ostr, bool detail=false) const |
Checks if a Poisson equation with *this as a source has been correctly solved. More... | |
| void | raccord (int n) |
Performs the 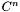 matching of the nucleus with respect to the first shell. More... matching of the nucleus with respect to the first shell. More... | |
| void | raccord_c1_zec (int puis, int nbre, int lmax) |
Performs the 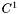 matching of the external domain with respect to the last shell using function like matching of the external domain with respect to the last shell using function like 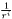 with with 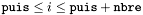 for each spherical harmonics with for each spherical harmonics with 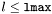 . More... . More... | |
| void | raccord_externe (int puis, int nbre, int lmax) |
| Matching of the external domain with the outermost shell. More... | |
Public Attributes | |
| Valeur | va |
The numerical value of the Cmp. More... | |
Private Member Functions | |
| void | import_gal (int nzet, const Cmp &ci) |
Assignment to another Cmp defined on a different mapping, when the two mappings do not have a particular relative orientation. More... | |
| void | import_align (int nzet, const Cmp &ci) |
Assignment to another Cmp defined on a different mapping, when the two mappings have aligned Cartesian axis. More... | |
| void | import_anti (int nzet, const Cmp &ci) |
Assignment to another Cmp defined on a different mapping, when the two mappings have anti-aligned Cartesian axis (i.e. More... | |
| void | import_align_symy (int nzet, const Cmp &ci) |
Assignment to another Cmp defined on a different mapping, when the two mappings have aligned Cartesian axis. More... | |
| void | import_anti_symy (int nzet, const Cmp &ci) |
Assignment to another Cmp defined on a different mapping, when the two mappings have anti-aligned Cartesian axis (i.e. More... | |
| void | import_align_asymy (int nzet, const Cmp &ci) |
Assignment to another Cmp defined on a different mapping, when the two mappings have aligned Cartesian axis. More... | |
| void | import_anti_asymy (int nzet, const Cmp &ci) |
Assignment to another Cmp defined on a different mapping, when the two mappings have anti-aligned Cartesian axis (i.e. More... | |
| void | del_t () |
| Logical destructor. More... | |
| void | del_deriv () |
| Logical destructor of the derivatives. More... | |
| void | set_der_0x0 () |
| Sets the pointers for derivatives to 0x0. More... | |
Private Attributes | |
| const Map * | mp |
| Reference mapping. More... | |
| int | etat |
Logical state (ETATNONDEF , ETATQCQ or ETATZERO ). More... | |
| int | dzpuis |
Power of r by which the quantity represented by this must be divided in the external compactified zone in order to get the correct physical values. More... | |
| Cmp * | p_dsdr |
Pointer on 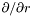 of of *this. More... | |
| Cmp * | p_srdsdt |
Pointer on 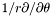 of of *this. More... | |
| Cmp * | p_srstdsdp |
Pointer on 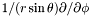 of of *this. More... | |
| Cmp * | p_dsdx |
Pointer on 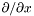 of of *this , where 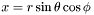 . More... . More... | |
| Cmp * | p_dsdy |
Pointer on 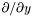 of of *this , where 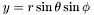 . More... . More... | |
| Cmp * | p_dsdz |
Pointer on 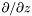 of of *this , where 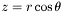 . More... . More... | |
| Cmp * | p_lap |
Pointer on the Laplacian of *this. More... | |
| int | ind_lap |
| Power of r by which the last computed Laplacian has been multiplied in the external compactified domain. More... | |
| Tbl * | p_integ |
Pointer on the space integral of *this (values in each domain) More... | |
Friends | |
| ostream & | operator<< (ostream &, const Cmp &) |
| Display. More... | |
Detailed Description
Component of a tensorial field *** DEPRECATED : use class Scalar instead ***.
()
Constructor & Destructor Documentation
◆ Cmp() [1/4]
|
explicit |
◆ Cmp() [2/4]
|
explicit |
◆ Cmp() [3/4]
| Lorene::Cmp::Cmp | ( | const Cmp & | a | ) |
◆ Cmp() [4/4]
Constructor from a file (see sauve(FILE*) )
Definition at line 237 of file cmp.C.
References dzpuis, etat, Lorene::fread_be(), Lorene::Map::get_mg(), and set_der_0x0().
◆ ~Cmp()
Member Function Documentation
◆ affiche_seuil()
| void Lorene::Cmp::affiche_seuil | ( | ostream & | ostr, |
| int | type = 0, |
||
| int | precision = 4, |
||
| double | threshold = 1.e-7 |
||
| ) | const |
Prints only the values greater than a given threshold.
- Parameters
-
ostr [input] Output stream used for the printing type [input] Type of display : 0 = prints only the coefficients, 1 = prints only the values in configuration space, 2 = prints both precision [input] Number of printed digits (default: 4) threshold [input] Value above which an array element is printed (default: 1.e-7)
Definition at line 615 of file cmp.C.
References etat.
◆ allocate_all()
| void Lorene::Cmp::allocate_all | ( | ) |
Sets the logical state to ETATQCQ (ordinary state) and performs the memory allocation of all the elements, down to the double arrays of the Tbl s.
This function performs in fact recursive calls to set_etat_qcq() on each element of the chain Cmp -> Valeur -> Mtbl -> Tbl .
Definition at line 326 of file cmp.C.
References Lorene::Valeur::c, Lorene::Mtbl::get_nzone(), Lorene::Valeur::set_etat_c_qcq(), Lorene::Mtbl::set_etat_qcq(), Lorene::Tbl::set_etat_qcq(), set_etat_qcq(), Lorene::Mtbl::t, and va.
◆ annule() [1/2]
| void Lorene::Cmp::annule | ( | int | l | ) |
◆ annule() [2/2]
| void Lorene::Cmp::annule | ( | int | l_min, |
| int | l_max | ||
| ) |
Sets the Cmp to zero in several domains.
- Parameters
-
l_min [input] The Cmpwill be set (logically) to zero in the domains whose indices are in the range[l_min,l_max].l_max [input] see the comments for l_min.
Note that annule(0,va.mg->get_nzone()-1) is equivalent to set_etat_zero() .
Definition at line 360 of file cmp.C.
References etat, Lorene::Mg3d::get_nzone(), Lorene::Valeur::mg, set_etat_zero(), and va.
◆ annule_hard()
| void Lorene::Cmp::annule_hard | ( | ) |
Sets the Cmp to zero in a hard way.
1/ Sets the logical state to ETATQCQ , i.e. to an ordinary state. 2/ Fills the Valeur va with zeros. NB: this function must be used for debugging purposes only. For other operations, the functions set_etat_zero() or annule(int, int) must be perferred.
Definition at line 341 of file cmp.C.
References Lorene::Valeur::annule_hard(), del_deriv(), etat, and va.
◆ asymptot()
| Valeur ** Lorene::Cmp::asymptot | ( | int | n, |
| const int | flag = 0 |
||
| ) | const |
Asymptotic expansion at r = infinity.
Determines the coefficients 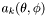 of the expansion
of the expansion
![\[ \sum_{k=0}^n {a_k(\theta, \phi) \over r^k} \]](form_150.png)
of *this when 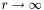 .
.
- Parameters
-
n order of the expansion flag : output
- Returns
- Array of n+1
Valeurs onmg->angu
describing the coefficients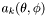 . This array is allocated by the routine.
. This array is allocated by the routine.
Definition at line 74 of file cmp_asymptot.C.
References Lorene::Map::get_mg(), Lorene::Mg3d::get_nzone(), Lorene::Mg3d::get_type_r(), and mp.
◆ check_dzpuis()
| bool Lorene::Cmp::check_dzpuis | ( | int | dzi | ) | const |
Returns false if the last domain is compactified and *this is not zero in this domain and dzpuis is not equal to dzi , otherwise return true.
Definition at line 718 of file cmp.C.
References dz_nonzero(), and dzpuis.
◆ dec2_dzpuis()
| void Lorene::Cmp::dec2_dzpuis | ( | ) |
Decreases by 2 the value of dzpuis and changes accordingly the values of the Cmp in the external compactified domain (ZEC).
Definition at line 183 of file cmp_r_manip.C.
References Lorene::Map::dec2_dzpuis(), mp, and operator=().
◆ dec_dzpuis()
| void Lorene::Cmp::dec_dzpuis | ( | ) |
Decreases by 1 the value of dzpuis and changes accordingly the values of the Cmp in the external compactified domain (ZEC).
Definition at line 157 of file cmp_r_manip.C.
References Lorene::Map::dec_dzpuis(), mp, and operator=().
◆ del_deriv()
|
private |
◆ del_t()
|
private |
Logical destructor.
Definition at line 262 of file cmp.C.
References del_deriv(), Lorene::Valeur::del_t(), etat, and va.
◆ deriv()
| const Cmp & Lorene::Cmp::deriv | ( | int | i | ) | const |
Returns 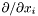 of
of *this , where 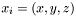 .
.
Note that in the external compactified domain (ZEC), it returns instead 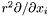 .
.
- Parameters
-
i [input] i=0 for x , i=1 for y , i=2 for z .
Definition at line 214 of file cmp_deriv.C.
◆ div_r()
| void Lorene::Cmp::div_r | ( | ) |
Division by r everywhere.
Definition at line 81 of file cmp_r_manip.C.
References Cmp(), del_deriv(), Lorene::Map::div_r(), mp, and operator=().
◆ dsdr()
| const Cmp & Lorene::Cmp::dsdr | ( | ) | const |
Returns 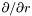 of
of *this .
Note that in the external compactified domain (ZEC), it returns instead 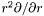 .
.
Definition at line 87 of file cmp_deriv.C.
References etat.
◆ dsdx()
| const Cmp & Lorene::Cmp::dsdx | ( | ) | const |
Returns 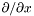 of
of *this , where 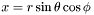 .
.
Note that in the external compactified domain (ZEC), it returns instead 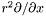 .
.
Definition at line 151 of file cmp_deriv.C.
References etat.
◆ dsdy()
| const Cmp & Lorene::Cmp::dsdy | ( | ) | const |
Returns 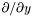 of
of *this , where 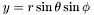 .
.
Note that in the external compactified domain (ZEC), it returns instead 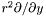 .
.
Definition at line 172 of file cmp_deriv.C.
References etat.
◆ dsdz()
| const Cmp & Lorene::Cmp::dsdz | ( | ) | const |
Returns 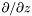 of
of *this , where 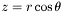 .
.
Note that in the external compactified domain (ZEC), it returns instead 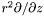 .
.
Definition at line 193 of file cmp_deriv.C.
References etat.
◆ dz_nonzero()
| bool Lorene::Cmp::dz_nonzero | ( | ) | const |
◆ filtre()
| void Lorene::Cmp::filtre | ( | int | n | ) |
Sets the n lasts coefficients in r to 0 in the external domain.
Definition at line 77 of file cmp_manip.C.
References etat.
◆ filtre_phi()
| void Lorene::Cmp::filtre_phi | ( | int | n, |
| int | zone | ||
| ) |
Sets the n lasts coefficients in 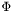 to 0 in the domain
to 0 in the domain zone .
Definition at line 104 of file cmp_manip.C.
References etat.
◆ fixe_decroissance()
| void Lorene::Cmp::fixe_decroissance | ( | int | puis | ) |
Substracts all the components behaving like 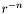 in the external domain, with n strictly lower than
in the external domain, with n strictly lower than puis , so that *this
decreases at least like 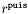 at infinity.
at infinity.
Definition at line 189 of file cmp_manip.C.
References Lorene::Valeur::base, Lorene::Valeur::c_cf, Lorene::Valeur::coef(), Lorene::cos(), dzpuis, Lorene::Map_af::get_alpha(), Lorene::Base_val::get_base_r(), Lorene::Map::get_mg(), Lorene::Mg3d::get_np(), Lorene::Mg3d::get_nr(), Lorene::Mg3d::get_nt(), Lorene::Mg3d::get_nzone(), mp, mult_r_zec(), Lorene::pow(), R_CHEBU, Lorene::Mtbl_cf::set(), Lorene::Valeur::set_etat_cf_qcq(), and va.
◆ get_dzpuis()
|
inline |
◆ get_etat()
|
inline |
◆ get_mp()
|
inline |
◆ import() [1/2]
| void Lorene::Cmp::import | ( | const Cmp & | ci | ) |
Assignment to another Cmp defined on a different mapping.
This assignment is performed point to point by means of the spectral expansion of the original Cmp .
- Parameters
-
ci [input] Cmpto be imported.
Definition at line 76 of file cmp_import.C.
References Lorene::Map::get_mg(), Lorene::Mg3d::get_nzone(), and mp.
◆ import() [2/2]
| void Lorene::Cmp::import | ( | int | nzet, |
| const Cmp & | ci | ||
| ) |
Assignment to another Cmp defined on a different mapping.
This assignment is performed point to point by means of the spectral expansion of the original Cmp .
- Parameters
-
nzet [input] Number of domains of the destination mapping (i.e. this->mp) where the importation is performed: the assignment is done for the domains whose indices are between 0 andnzet-1. In the other domains,*thisis set to zero.ci [input] Cmpto be imported.
Definition at line 88 of file cmp_import.C.
References Lorene::Map::get_bvect_cart(), import_align(), import_anti(), import_gal(), and mp.
◆ import_align()
|
private |
Assignment to another Cmp defined on a different mapping, when the two mappings have aligned Cartesian axis.
This assignment is performed point to point by means of the spectral expansion of the original Cmp .
- Parameters
-
nzet [input] Number of domains of the destination mapping (i.e. this->mp) where the importation is performed: the assignment is done for the domains whose indices are between 0 andnzet-1. In the other domains,*thisis set to zero.ci [input] Cmpto be imported.
Definition at line 530 of file cmp_import.C.
References etat.
◆ import_align_asymy()
|
private |
Assignment to another Cmp defined on a different mapping, when the two mappings have aligned Cartesian axis.
Case where the Cmp is antisymmetric with respect to the plane y=0.
This assignment is performed point to point by means of the spectral expansion of the original Cmp .
- Parameters
-
nzet [input] Number of domains of the destination mapping (i.e. this->mp) where the importation is performed: the assignment is done for the domains whose indices are between 0 andnzet-1. In the other domains,*thisis set to zero.ci [input] Cmpto be imported.
Definition at line 372 of file cmp_import_asymy.C.
References etat.
◆ import_align_symy()
|
private |
Assignment to another Cmp defined on a different mapping, when the two mappings have aligned Cartesian axis.
Case where the Cmp is symmetric with respect to the plane y=0.
This assignment is performed point to point by means of the spectral expansion of the original Cmp .
- Parameters
-
nzet [input] Number of domains of the destination mapping (i.e. this->mp) where the importation is performed: the assignment is done for the domains whose indices are between 0 andnzet-1. In the other domains,*thisis set to zero.ci [input] Cmpto be imported.
Definition at line 343 of file cmp_import_symy.C.
References etat.
◆ import_anti()
|
private |
Assignment to another Cmp defined on a different mapping, when the two mappings have anti-aligned Cartesian axis (i.e.
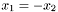 ,
, 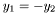 ,
, 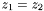 ).
).
This assignment is performed point to point by means of the spectral expansion of the original Cmp .
- Parameters
-
nzet [input] Number of domains of the destination mapping (i.e. this->mp) where the importation is performed: the assignment is done for the domains whose indices are between 0 andnzet-1. In the other domains,*thisis set to zero.ci [input] Cmpto be imported.
Definition at line 338 of file cmp_import.C.
References etat.
◆ import_anti_asymy()
|
private |
Assignment to another Cmp defined on a different mapping, when the two mappings have anti-aligned Cartesian axis (i.e.
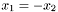 ,
, 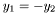 ,
, 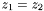 ). Case where the
). Case where the Cmp is antisymmetric with respect to the plane y=0.
This assignment is performed point to point by means of the spectral expansion of the original Cmp .
- Parameters
-
nzet [input] Number of domains of the destination mapping (i.e. this->mp) where the importation is performed: the assignment is done for the domains whose indices are between 0 andnzet-1. In the other domains,*thisis set to zero.ci [input] Cmpto be imported.
Definition at line 129 of file cmp_import_asymy.C.
References etat.
◆ import_anti_symy()
|
private |
Assignment to another Cmp defined on a different mapping, when the two mappings have anti-aligned Cartesian axis (i.e.
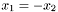 ,
, 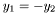 ,
, 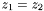 ). Case where the
). Case where the Cmp is symmetric with respect to the plane y=0.
This assignment is performed point to point by means of the spectral expansion of the original Cmp .
- Parameters
-
nzet [input] Number of domains of the destination mapping (i.e. this->mp) where the importation is performed: the assignment is done for the domains whose indices are between 0 andnzet-1. In the other domains,*thisis set to zero.ci [input] Cmpto be imported.
Definition at line 129 of file cmp_import_symy.C.
References etat.
◆ import_asymy() [1/2]
| void Lorene::Cmp::import_asymy | ( | const Cmp & | ci | ) |
Assignment to another Cmp defined on a different mapping.
Case where the Cmp is antisymmetric with respect to the plane y=0. This assignment is performed point to point by means of the spectral expansion of the original Cmp .
- Parameters
-
ci [input] Cmpto be imported.
Definition at line 70 of file cmp_import_asymy.C.
References Lorene::Map::get_mg(), Lorene::Mg3d::get_nzone(), and mp.
◆ import_asymy() [2/2]
| void Lorene::Cmp::import_asymy | ( | int | nzet, |
| const Cmp & | ci | ||
| ) |
Assignment to another Cmp defined on a different mapping.
Case where the Cmp is antisymmetric with respect to the plane y=0. This assignment is performed point to point by means of the spectral expansion of the original Cmp .
- Parameters
-
nzet [input] Number of domains of the destination mapping (i.e. this->mp) where the importation is performed: the assignment is done for the domains whose indices are between 0 andnzet-1. In the other domains,*thisis set to zero.ci [input] Cmpto be imported.
Definition at line 82 of file cmp_import_asymy.C.
References Lorene::Map::get_bvect_cart(), import_align_asymy(), import_anti_asymy(), and mp.
◆ import_gal()
|
private |
Assignment to another Cmp defined on a different mapping, when the two mappings do not have a particular relative orientation.
This assignment is performed point to point by means of the spectral expansion of the original Cmp .
- Parameters
-
nzet [input] Number of domains of the destination mapping (i.e. this->mp) where the importation is performed: the assignment is done for the domains whose indices are between 0 andnzet-1. In the other domains,*thisis set to zero.ci [input] Cmpto be imported.
Definition at line 139 of file cmp_import.C.
◆ import_symy() [1/2]
| void Lorene::Cmp::import_symy | ( | const Cmp & | ci | ) |
Assignment to another Cmp defined on a different mapping.
Case where the Cmp is symmetric with respect to the plane y=0. This assignment is performed point to point by means of the spectral expansion of the original Cmp .
- Parameters
-
ci [input] Cmpto be imported.
Definition at line 70 of file cmp_import_symy.C.
References Lorene::Map::get_mg(), Lorene::Mg3d::get_nzone(), and mp.
◆ import_symy() [2/2]
| void Lorene::Cmp::import_symy | ( | int | nzet, |
| const Cmp & | ci | ||
| ) |
Assignment to another Cmp defined on a different mapping.
Case where the Cmp is symmetric with respect to the plane y=0. This assignment is performed point to point by means of the spectral expansion of the original Cmp .
- Parameters
-
nzet [input] Number of domains of the destination mapping (i.e. this->mp) where the importation is performed: the assignment is done for the domains whose indices are between 0 andnzet-1. In the other domains,*thisis set to zero.ci [input] Cmpto be imported.
Definition at line 82 of file cmp_import_symy.C.
References Lorene::Map::get_bvect_cart(), import_align_symy(), import_anti_symy(), and mp.
◆ inc2_dzpuis()
| void Lorene::Cmp::inc2_dzpuis | ( | ) |
Increases by 2 the value of dzpuis and changes accordingly the values of the Cmp in the external compactified domain (ZEC).
Definition at line 195 of file cmp_r_manip.C.
References Lorene::Map::inc2_dzpuis(), mp, and operator=().
◆ inc_dzpuis()
| void Lorene::Cmp::inc_dzpuis | ( | ) |
Increases by the value of dzpuis and changes accordingly the values of the Cmp in the external compactified domain (ZEC).
Definition at line 169 of file cmp_r_manip.C.
References Lorene::Map::inc_dzpuis(), mp, and operator=().
◆ integrale()
| double Lorene::Cmp::integrale | ( | ) | const |
Computes the integral over all space of *this .
The computed quantity is (u being the field represented by *this ) 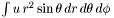 . Note that in the external compactified domain (ZEC),
. Note that in the external compactified domain (ZEC), dzpuis
must be 4 for the computation to take place.
Definition at line 58 of file cmp_integ.C.
References Lorene::Map::get_mg(), Lorene::Mg3d::get_nzone(), integrale_domains(), and mp.
◆ integrale_domains()
| const Tbl & Lorene::Cmp::integrale_domains | ( | ) | const |
Computes the integral in each domain of *this .
The computed quantity is (u being the field represented by *this ) 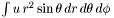 in each domain. The result is returned a
in each domain. The result is returned a Tbl on the various domains. Note that in the external compactified domain (ZEC), dzpuis
must be 4 for the computation to take place.
Definition at line 76 of file cmp_integ.C.
References etat.
◆ laplacien()
| const Cmp & Lorene::Cmp::laplacien | ( | int | zec_mult_r = 4 | ) | const |
Returns the Laplacian of *this.
- Parameters
-
zec_mult_r [input] Determines the quantity computed in the external compactified domain (ZEC) (u in the field represented by *this) : \ zec_mult_r = 0 :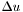 \ zec_mult_r = 2 :
\ zec_mult_r = 2 : 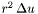 \ zec_mult_r = 4 (default) :
\ zec_mult_r = 4 (default) : 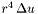
Definition at line 245 of file cmp_deriv.C.
References etat.
◆ mult_cost()
| void Lorene::Cmp::mult_cost | ( | ) |
Multiplication by $.
Definition at line 131 of file cmp_r_manip.C.
References del_deriv(), mp, Lorene::Map::mult_cost(), and operator=().
◆ mult_r()
| void Lorene::Cmp::mult_r | ( | ) |
Multiplication by r everywhere.
Definition at line 94 of file cmp_r_manip.C.
References del_deriv(), mp, and Lorene::Map::mult_r().
◆ mult_r_zec()
| void Lorene::Cmp::mult_r_zec | ( | ) |
Multiplication by r in the external compactified domain (ZEC)
Definition at line 106 of file cmp_r_manip.C.
References del_deriv(), mp, Lorene::Map::mult_r_zec(), and operator=().
◆ mult_rsint()
| void Lorene::Cmp::mult_rsint | ( | ) |
Multiplication by 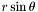 .
.
Definition at line 119 of file cmp_r_manip.C.
References del_deriv(), mp, Lorene::Map::mult_rsint(), and operator=().
◆ multipole_spectrum()
| Tbl Lorene::Cmp::multipole_spectrum | ( | ) |
Gives the spectrum in terms of multipolar modes l .
- Returns
- a
Tblof size (nzone, lmax), where lmax is the maximal multipolar momentum over all domains. The l -th element contains the L1 norm of the l -th multipole (i.e. a sum over all m of the norms (coefficient space) of the component of a given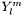 .
.
Definition at line 765 of file cmp.C.
References etat.
◆ operator()() [1/2]
|
inline |
◆ operator()() [2/2]
|
inline |
◆ operator*=()
| void Lorene::Cmp::operator*= | ( | const Cmp & | ci | ) |
◆ operator+=()
| void Lorene::Cmp::operator+= | ( | const Cmp & | ci | ) |
◆ operator-=()
| void Lorene::Cmp::operator-= | ( | const Cmp & | ci | ) |
◆ operator=() [1/5]
| void Lorene::Cmp::operator= | ( | const Cmp & | a | ) |
◆ operator=() [2/5]
| void Lorene::Cmp::operator= | ( | const Valeur & | a | ) |
Assignment to a Valeur.
Definition at line 446 of file cmp.C.
References Lorene::Valeur::get_etat(), and va.
◆ operator=() [3/5]
| void Lorene::Cmp::operator= | ( | const Mtbl & | a | ) |
◆ operator=() [4/5]
| void Lorene::Cmp::operator= | ( | double | x | ) |
Assignment to a double.
Definition at line 529 of file cmp.C.
References del_deriv(), dzpuis, set_etat_qcq(), set_etat_zero(), and va.
◆ operator=() [5/5]
| void Lorene::Cmp::operator= | ( | int | n | ) |
Assignment to an int.
Definition at line 545 of file cmp.C.
References del_deriv(), dzpuis, set_etat_qcq(), set_etat_zero(), and va.
◆ poisson() [1/2]
| Cmp Lorene::Cmp::poisson | ( | ) | const |
Solves the scalar Poisson equation with *this as a source.
The source  of the equation
of the equation 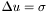 is represented by the
is represented by the Cmp *this . Note that dzpuis must be equal to 2, 3 or 4, i.e. that the quantity stored in *this is in fact 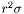 or
or 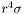 in the external compactified domain. The solution u with the boundary condition u =0 at spatial infinity is the returned
in the external compactified domain. The solution u with the boundary condition u =0 at spatial infinity is the returned Cmp .
Definition at line 97 of file cmp_pde.C.
References mp, and Lorene::Map::poisson().
◆ poisson() [2/2]
Solves the scalar Poisson equation with *this as a source (version with parameters to control the resolution).
The source  of the equation
of the equation 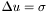 is represented by the
is represented by the Cmp *this . Note that dzpuis must be equal to 2 or 4, i.e. that the quantity stored in *this is in fact 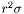 or
or 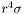 in the external compactified domain.
in the external compactified domain.
- Parameters
-
par [input/output] possible parameters uu [input/output] solution u with the boundary condition u =0 at spatial infinity.
Definition at line 110 of file cmp_pde.C.
References mp, and Lorene::Map::poisson().
◆ poisson_dirichlet()
Is identicall to Cmp::poisson() .
The regularity condition at the origin is replace by a boundary condition of the Dirichlet type.
- Parameters
-
limite [input] : angular function. The boundary condition is given by limite[num] .num [input] : index of the boudary at which the condition is to be fullfilled.
More precisely we impose the solution is equal to limite[num] at the boundary between the domains num and num+1 (the latter one being a shell).
Definition at line 98 of file cmp_pde_frontiere.C.
References mp, and Lorene::Map::poisson_frontiere().
◆ poisson_neumann()
Idem as Cmp::poisson_dirichlet , the boundary condition being on the radial derivative of the solution.
Definition at line 106 of file cmp_pde_frontiere.C.
References mp, and Lorene::Map::poisson_frontiere().
◆ poisson_neumann_interne()
Idem as Cmp::poisson_neumann , the boundary condition is on the radial derivative of the solution.
But in this method, the poisson equation is solved in the shell only. We have so to impose a boundary condition on the surface of the star. This is used for example to solve the continuity equation for the fluid in the star.
Definition at line 113 of file cmp_pde_frontiere.C.
References mp, and Lorene::Map::poisson_interne().
◆ poisson_regular()
| void Lorene::Cmp::poisson_regular | ( | int | k_div, |
| int | nzet, | ||
| double | unsgam1, | ||
| Param & | par, | ||
| Cmp & | uu, | ||
| Cmp & | uu_regu, | ||
| Cmp & | uu_div, | ||
| Tenseur & | duu_div, | ||
| Cmp & | source_regu, | ||
| Cmp & | source_div | ||
| ) | const |
Solves the scalar Poisson equation with *this as a source (version with parameters to control the resolution).
The source  of the equation
of the equation 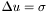 is represented by the
is represented by the Cmp *this . The regularized source 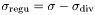 is constructed and solved. Note that
is constructed and solved. Note that dzpuis must be equal to 2 or 4, i.e. that the quantity stored in *this is in fact 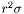 or
or 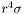 in the external compactified domain.
in the external compactified domain.
- Parameters
-
k_div [input] regularization degree of the procedure nzet [input] number of domains covering the star unsgam1 [input] parameter 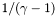 where
where  denotes the adiabatic index
denotes the adiabatic index par [input/output] possible parameters uu [input/output] solution uu_regu [output] solution of the regular part of the source. uu_div [output] solution of the diverging part of the source. duu_div [output] derivative of the diverging potential. source_regu [output] regularized source source_div [output] diverging part of the source
Definition at line 91 of file cmp_poisson_regu.C.
References mp, and Lorene::Map::poisson_regular().
◆ poisson_tau() [1/2]
| Cmp Lorene::Cmp::poisson_tau | ( | ) | const |
Same as Poisson with a Tau method.
Definition at line 123 of file cmp_pde.C.
References mp, and Lorene::Map::poisson_tau().
◆ poisson_tau() [2/2]
Same as Poisson with a Tau method.
Definition at line 136 of file cmp_pde.C.
References mp, and Lorene::Map::poisson_tau().
◆ raccord()
| void Lorene::Cmp::raccord | ( | int | n | ) |
Performs the 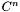 matching of the nucleus with respect to the first shell.
matching of the nucleus with respect to the first shell.
Definition at line 173 of file cmp_raccord.C.
References etat.
◆ raccord_c1_zec()
| void Lorene::Cmp::raccord_c1_zec | ( | int | puis, |
| int | nbre, | ||
| int | lmax | ||
| ) |
Performs the 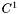 matching of the external domain with respect to the last shell using function like
matching of the external domain with respect to the last shell using function like 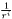 with
with 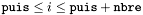 for each spherical harmonics with
for each spherical harmonics with 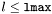 .
.
Definition at line 87 of file cmp_raccord_zec.C.
References etat.
◆ raccord_externe()
| void Lorene::Cmp::raccord_externe | ( | int | puis, |
| int | nbre, | ||
| int | lmax | ||
| ) |
Matching of the external domain with the outermost shell.
Definition at line 94 of file cmp_raccord_externe.C.
References Lorene::Tbl::annule_hard(), Lorene::Valeur::base, Lorene::Valeur::c_cf, Lorene::Valeur::coef(), Lorene::cos(), Lorene::Map_af::get_alpha(), Lorene::Map_af::get_beta(), Lorene::Map::get_mg(), Lorene::Mg3d::get_np(), Lorene::Mg3d::get_nr(), Lorene::Mg3d::get_nt(), Lorene::Mg3d::get_nzone(), mp, Lorene::pow(), Lorene::Matrice::set(), Lorene::Tbl::set(), Lorene::Mtbl_cf::set(), set_dzpuis(), Lorene::Valeur::set_etat_cf_qcq(), Lorene::Matrice::set_etat_qcq(), Lorene::Mtbl_cf::set_etat_qcq(), Lorene::Tbl::set_etat_qcq(), Lorene::sqrt(), Lorene::Mtbl_cf::t, va, Lorene::Valeur::ylm(), and Lorene::Valeur::ylm_i().
◆ sauve()
| void Lorene::Cmp::sauve | ( | FILE * | fd | ) | const |
Save in a file.
Definition at line 564 of file cmp.C.
References dzpuis, etat, Lorene::fwrite_be(), Lorene::Valeur::sauve(), and va.
◆ set() [1/2]
|
inline |
Read/write of the value in a given domain.
NB: to gain in efficiency, the method del_deriv() (to delete the derived members) is not called by this function. It must thus be invoqued by the user.
- Parameters
-
l [input] domain index
- Returns
- Tbl containing the value of the field in domain
l.
Definition at line 724 of file cmp.h.
References etat.
◆ set() [2/2]
|
inline |
Read/write of a particular element.
NB: to gain in efficiency, the method del_deriv() (to delete the derived members) is not called by this function. It must thus be invoqued by the user.
- Parameters
-
l [input] domain index k [input]  index
index j [input]  index
index i [input] r (  ) index
) index
Definition at line 749 of file cmp.h.
References etat.
◆ set_der_0x0()
|
private |
◆ set_dzpuis()
| void Lorene::Cmp::set_dzpuis | ( | int | dzi | ) |
◆ set_etat_nondef()
| void Lorene::Cmp::set_etat_nondef | ( | ) |
◆ set_etat_qcq()
| void Lorene::Cmp::set_etat_qcq | ( | ) |
◆ set_etat_zero()
| void Lorene::Cmp::set_etat_zero | ( | ) |
◆ set_val_hor()
| void Lorene::Cmp::set_val_hor | ( | double | val, |
| int | zone | ||
| ) |
Sets the value of the Cmp to val on the inner boudary of the shell number zone .This is usefull for dealing with undefined values.
Definition at line 162 of file cmp_manip.C.
References etat.
◆ set_val_inf()
| void Lorene::Cmp::set_val_inf | ( | double | val | ) |
Sets the value of the Cmp to val at infinity.
This is usefull for dealing with undefined values. The external domain must be compactified.
Definition at line 129 of file cmp_manip.C.
References etat.
◆ srdsdt()
| const Cmp & Lorene::Cmp::srdsdt | ( | ) | const |
Returns 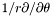 of
of *this .
Note that in the external compactified domain (ZEC), it returns instead 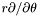 .
.
Definition at line 108 of file cmp_deriv.C.
References etat.
◆ srstdsdp()
| const Cmp & Lorene::Cmp::srstdsdp | ( | ) | const |
Returns 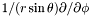 of
of *this .
Note that in the external compactified domain (ZEC), it returns instead 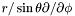 .
.
Definition at line 130 of file cmp_deriv.C.
References etat.
◆ std_base_scal()
| void Lorene::Cmp::std_base_scal | ( | ) |
Sets the spectral bases of the Valeur va to the standard ones for a scalar.
Definition at line 647 of file cmp.C.
References Lorene::Valeur::std_base_scal(), and va.
◆ test_poisson()
Checks if a Poisson equation with *this as a source has been correctly solved.
- Parameters
-
uu [input] Solution u of the Poisson equation 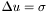 ,
,  being represented by the
being represented by the Cmp*this.ostr [input/output] Output stream used for displaying err.detail [input] - if
truedisplayserr(0,*),err(1,*)anderr(2,*) - if
false(default), displays only the relative errorerr(0,*).
- if
- Returns
- 2-D
Tblerrdecribing the errors in each domain:err(0,l): Relative error in domain no.l, defined as the maximum value of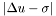 in that domain divided by m , where m is the maximum value of
in that domain divided by m , where m is the maximum value of 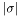 over all domains if
over all domains if dzpuis= 0} or is zero in the external compactified domain (ECD). If
is zero in the external compactified domain (ECD). If dzpuis!= 0} and does not vanish in the ECD, the value of m used in the non-compactified domains is the maximum value over these domains, whereas the value of m used in the external compactified domain is the maximum value on that particular domain.
does not vanish in the ECD, the value of m used in the non-compactified domains is the maximum value over these domains, whereas the value of m used in the external compactified domain is the maximum value on that particular domain. err(1,l): Maximum value of the absolute error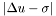 in domain no.
in domain no. l
err(2,l): Maximum value of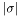 in domain no.
in domain no. l
Definition at line 61 of file cmp_test_poisson.C.
References Lorene::abs(), check_dzpuis(), dzpuis, Lorene::Map::get_mg(), get_mp(), Lorene::Mg3d::get_nzone(), laplacien(), Lorene::max(), mp, Lorene::Tbl::set(), and Lorene::Tbl::set_etat_qcq().
◆ val_point()
| double Lorene::Cmp::val_point | ( | double | r, |
| double | theta, | ||
| double | phi | ||
| ) | const |
Computes the value of the field represented by *this at an arbitrary point 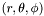 , by means of the spectral expansion.
, by means of the spectral expansion.
- Parameters
-
r [input] value of the coordinate r theta [input] value of the coordinate 
phi [input] value of the coordinate 
- Returns
- value at the point
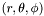 of the field represented by
of the field represented by *this.
Definition at line 735 of file cmp.C.
References etat.
Friends And Related Function Documentation
◆ operator<<
|
friend |
Member Data Documentation
◆ dzpuis
|
private |
◆ etat
|
private |
◆ ind_lap
|
mutableprivate |
◆ mp
◆ p_dsdr
◆ p_dsdx
|
mutableprivate |
◆ p_dsdy
|
mutableprivate |
◆ p_dsdz
|
mutableprivate |
◆ p_integ
|
mutableprivate |
◆ p_lap
|
mutableprivate |
◆ p_srdsdt
|
mutableprivate |
◆ p_srstdsdp
|
mutableprivate |
◆ va
The documentation for this class was generated from the following files:
