Tensor handling *** DEPRECATED : use class Tensor instead ***.
More...
#include <tenseur.h>

Public Member Functions | |
| Tenseur (const Map &map, const Metrique *met=0x0, double weight=0) | |
| Constructor for a scalar field. More... | |
| Tenseur (const Cmp &cmp, const Metrique *met=0x0, double weight=0) | |
Constructor for a scalar field and from a Cmp . More... | |
| Tenseur (const Map &map, int val, const Itbl &tipe, const Base_vect &triad_i, const Metrique *met=0x0, double weight=0) | |
| Standard constructor. More... | |
| Tenseur (const Map &map, int val, const Itbl &tipe, const Base_vect *triad_i, const Metrique *met=0x0, double weight=0) | |
| Standard constructor with the triad passed as a pointer. More... | |
| Tenseur (const Map &map, int val, int tipe, const Base_vect &triad_i, const Metrique *met=0x0, double weight=0) | |
| Standard constructor when all the indices are of the same type. More... | |
| Tenseur (const Tenseur &) | |
| Copy constructor. More... | |
| Tenseur (const Tenseur_sym &) | |
| Constructor from a symmetric tensor. More... | |
| Tenseur (const Map &map, const Base_vect &triad_i, FILE *fich, const Metrique *met=0x0) | |
Constructor from a file (see sauve(FILE*) ). More... | |
| Tenseur (const Map &map, FILE *fich, const Metrique *met=0x0) | |
Constructor from a file for a scalar field (see sauve(FILE*) ). More... | |
| virtual | ~Tenseur () |
| Destructor. More... | |
| void | set_etat_nondef () |
Sets the logical state to ETATNONDEF (undefined state). More... | |
| void | set_etat_zero () |
Sets the logical state to ETATZERO (zero state). More... | |
| void | set_etat_qcq () |
Sets the logical state to ETATQCQ (ordinary state). More... | |
| void | allocate_all () |
Sets the logical state to ETATQCQ (ordinary state) and performs the memory allocation of all the elements, down to the double arrays of the Tbl s. More... | |
| void | change_triad (const Base_vect &new_triad) |
| Sets a new vectorial basis (triad) of decomposition and modifies the components accordingly. More... | |
| void | set_triad (const Base_vect &new_triad) |
| Assigns a new vectorial basis (triad) of decomposition. More... | |
| void | set_poids (double weight) |
| Sets the weight for a tensor density. More... | |
| void | set_metric (const Metrique &met) |
| Sets the pointer on the metric for a tensor density. More... | |
| virtual void | operator= (const Tenseur &tens) |
Assignment to another Tenseur. More... | |
| void | operator= (const Cmp &field) |
Assignment to a Cmp (scalar field only) More... | |
| void | operator= (double) |
Assignment to a double (scalar field only, except for zero) More... | |
| void | operator= (int) |
Assignment to a int (scalar field only, except for zero) More... | |
| Cmp & | set () |
Read/write for a scalar (see also operator=(const Cmp&) ). More... | |
| Cmp & | set (int) |
| Read/write for a vector. More... | |
| Cmp & | set (int, int) |
| Read/write for a tensor of valence 2. More... | |
| Cmp & | set (int, int, int) |
| Read/write for a tensor of valence 3. More... | |
| Cmp & | set (const Itbl &) |
| Read/write in the general case. More... | |
| void | annule (int l) |
Sets the Tenseur to zero in a given domain. More... | |
| void | annule (int l_min, int l_max) |
Sets the Tenseur to zero in several domains. More... | |
| void | set_std_base () |
| Set the standard spectal basis of decomposition for each component. More... | |
| void | dec_dzpuis () |
| dzpuis -= 1 ; More... | |
| void | inc_dzpuis () |
| dzpuis += 1 ; More... | |
| void | dec2_dzpuis () |
| dzpuis -= 2 ; More... | |
| void | inc2_dzpuis () |
| dzpuis += 2 ; More... | |
| void | mult_r_zec () |
| Multiplication by r in the external zone. More... | |
| Tenseur | inverse_poisson_vect (double lambda) const |
Compute 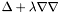 of of *this , *this being of valence 1. More... | |
| virtual int | donne_place (const Itbl &idx) const |
Returns the position in the Cmp 1-D array c of a component given by its indices. More... | |
| virtual Itbl | donne_indices (int place) const |
Returns the indices of a component given by its position in the Cmp 1-D array c . More... | |
| const Map * | get_mp () const |
| Returns pointer on the mapping. More... | |
| const Base_vect * | get_triad () const |
| Returns the vectorial basis (triad) on which the components are defined. More... | |
| int | get_etat () const |
| Returns the logical state. More... | |
| int | get_valence () const |
| Returns the valence. More... | |
| int | get_n_comp () const |
| Returns the number of components. More... | |
| int | get_type_indice (int i) const |
Returns the type of the index number i . More... | |
| Itbl | get_type_indice () const |
| Returns the types of all the indices. More... | |
| double | get_poids () const |
| Returns the weight. More... | |
| const Metrique * | get_metric () const |
| Returns a pointer on the metric defining the conformal factor for tensor densities. More... | |
| const Cmp & | operator() () const |
| Read only for a scalar. More... | |
| const Cmp & | operator() (int) const |
| Read only for a vector. More... | |
| const Cmp & | operator() (int, int) const |
| Read only for a tensor of valence 2. More... | |
| const Cmp & | operator() (int, int, int) const |
| Read only for a tensor of valence 3. More... | |
| const Cmp & | operator() (const Itbl &) const |
| Read only in the general case. More... | |
| void | sauve (FILE *) const |
| Save in a file. More... | |
| const Tenseur & | gradient () const |
Returns the gradient of *this (Cartesian coordinates) More... | |
| const Tenseur & | gradient_spher () const |
Returns the gradient of *this (Spherical coordinates) (scalar field only). More... | |
| const Tenseur & | derive_cov (const Metrique &met) const |
Returns the covariant derivative of *this , with respect to met . More... | |
| const Tenseur & | derive_con (const Metrique &) const |
Returns the contravariant derivative of *this , with respect to met . More... | |
| const Tenseur & | carre_scal (const Metrique &) const |
Returns the scalar square of *this , with respect to met . More... | |
| void | poisson_vect (double lambda, Param &par, Tenseur &shift, Tenseur &vect, Tenseur &scal, bool verbose=true) const |
Solves the vectorial Poisson equation : 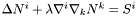 . More... . More... | |
| void | poisson_vect_tau (double lambda, Param &par, Tenseur &shift, Tenseur &vect, Tenseur &scal) const |
| void | poisson_vect_falloff (double lambda, Param &par, Tenseur &shift, Tenseur &vect, Tenseur &scal, int *k_falloff) const |
| void | poisson_vect_ylm (double lambda, Param ¶, Tenseur &shift, Tenseur &vecteur, Tenseur &scalaire, int nylm, double *intvec) const |
| Tenseur | poisson_vect (double lambda, Tenseur &vect, Tenseur &scal) const |
Solves the vectorial Poisson equation 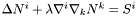 . More... . More... | |
| Tenseur | poisson_vect_tau (double lambda, Tenseur &vect, Tenseur &scal) const |
| Tenseur | poisson_vect_falloff (double lambda, Tenseur &vect, Tenseur &scal, int *k_falloff) const |
| Tenseur | poisson_vect_ylm (double lambda, Tenseur &vecteur, Tenseur &scalaire, int nylm, double *intvec) const |
| void | poisson_vect_oohara (double lambda, Param &par, Tenseur &shift, Tenseur &scal) const |
Solves the vectorial Poisson equation 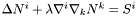 . More... . More... | |
| void | poisson_vect_oohara_tau (double lambda, Param &par, Tenseur &shift, Tenseur &scal) const |
| Tenseur | poisson_vect_oohara (double lambda, Tenseur &scal) const |
Solves the vectorial Poisson equation 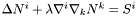 . More... . More... | |
| Tenseur | poisson_vect_oohara_tau (double lambda, Tenseur &scal) const |
| void | poisson_vect_regu (int k_div, int nzet, double unsgam1, double lambda, Param &par, Tenseur &shift, Tenseur &vect, Tenseur &scal) const |
Solves the vectorial Poisson equation : 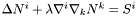 . More... . More... | |
Protected Member Functions | |
| bool | verif () const |
| Returns false for a tensor density without a defined metric. More... | |
| void | new_der_met () |
Builds the arrays met_depend , p_derive_cov , p_derive_con and p_carre_scal and fills them with null pointers. More... | |
| Tenseur (const Map &map, int val, const Itbl &tipe, int n_comp, const Base_vect &triad_i, const Metrique *met=0x0, double weight=0) | |
| Constructor used by the derived classes. More... | |
| Tenseur (const Map &, int val, int tipe, int n_comp, const Base_vect &triad_i, const Metrique *met=0x0, double weight=0) | |
| Constructor used by the derived classes when all the indices are of the same type. More... | |
| void | del_t () |
| Logical destructor. More... | |
| void | del_derive_met (int i) const |
Logical destructor of the derivatives depending on the i-th element of *met_depend . More... | |
| void | del_derive () const |
| Logical destructor of all the derivatives. More... | |
| void | set_der_met_0x0 (int i) const |
Sets the pointers of the derivatives depending on the i-th element of *met_depend to zero (as well as that i-th element). More... | |
| void | set_der_0x0 () const |
| Sets the pointers of all the derivatives to zero. More... | |
| virtual void | fait_gradient () const |
Calculates, if needed, the gradient of *this . More... | |
| void | fait_gradient_spher () const |
Calculates, if needed, the gradient of *this in a spherical orthonormal basis (scalar field only). More... | |
| virtual void | fait_derive_cov (const Metrique &met, int i) const |
Calculates, if needed, the covariant derivative of *this , with respect to met . More... | |
| virtual void | fait_derive_con (const Metrique &, int i) const |
Calculates, if needed, the contravariant derivative of *this , with respect to met . More... | |
| void | fait_carre_scal (const Metrique &, int i) const |
Calculates, if needed, the scalar square of *this , with respect to met . More... | |
| void | set_dependance (const Metrique &met) const |
To be used to describe the fact that the derivatives members have been calculated with met . More... | |
| int | get_place_met (const Metrique &metre) const |
Returns the position of the pointer on metre in the array met_depend . More... | |
Protected Attributes | |
| const Map *const | mp |
| Reference mapping. More... | |
| int | valence |
| Valence. More... | |
| const Base_vect * | triad |
| Vectorial basis (triad) with respect to which the tensor components are defined. More... | |
| Itbl | type_indice |
Array of size valence contening the type of each index, COV for a covariant one and CON for a contravariant one. More... | |
| int | n_comp |
| Number of components, depending on the symmetry. More... | |
| int | etat |
Logical state ETATZERO , ETATQCQ or ETATNONDEF. More... | |
| Cmp ** | c |
| The components. More... | |
| double | poids |
| For tensor densities: the weight. More... | |
| const Metrique * | metric |
| For tensor densities: the metric defining the conformal factor. More... | |
| const Metrique ** | met_depend |
Array of pointers on the Metrique 's used to calculate derivatives members. More... | |
| Tenseur * | p_gradient |
Pointer on the gradient of *this . More... | |
| Tenseur * | p_gradient_spher |
Pointer on the gradient of *this in a spherical orthonormal basis (scalar field only). More... | |
| Tenseur ** | p_derive_cov |
Array of pointers on the covariant derivatives of *this with respect to the corresponding metric in *met_depend . More... | |
| Tenseur ** | p_derive_con |
Array of pointers on the contravariant derivatives of *this with respect to the corresponding metric in *met_depend . More... | |
| Tenseur ** | p_carre_scal |
Array of pointers on the scalar squares of *this with respect to the corresponding metric in *met_depend . More... | |
Friends | |
| class | Tenseur_sym |
| class | Metrique |
| ostream & | operator<< (ostream &, const Tenseur &) |
| Tenseur | operator* (const Tenseur &, const Tenseur &) |
| Tensorial product. More... | |
| Tenseur | operator% (const Tenseur &, const Tenseur &) |
| Tensorial product with desaliasing. More... | |
| Tenseur | contract (const Tenseur &, int id1, int id2) |
Self contraction of two indices of a Tenseur . More... | |
| Tenseur | contract (const Tenseur &, int id1, const Tenseur &, int id2) |
Contraction of two Tenseur . More... | |
| Tenseur | contract_desal (const Tenseur &, int id1, const Tenseur &, int id2) |
| Tenseur | flat_scalar_prod (const Tenseur &t1, const Tenseur &t2) |
Scalar product of two Tenseur when the metric is 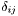 : performs the contraction of the last index of : performs the contraction of the last index of t1 with the first one of t2 , irrespective of the type of these indices. More... | |
| Tenseur | flat_scalar_prod_desal (const Tenseur &t1, const Tenseur &t2) |
Same as flat_scalar_prod but with desaliasing. More... | |
| Tenseur | manipule (const Tenseur &, const Metrique &, int idx) |
Raise or lower the index idx depending on its type, using the given Metrique . More... | |
| Tenseur | manipule (const Tenseur &, const Metrique &) |
Raise or lower all the indices, depending on their type, using the given Metrique . More... | |
| Tenseur | skxk (const Tenseur &) |
Contraction of the last index of (*this) with 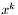 or or 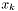 , depending on the type of S . More... , depending on the type of S . More... | |
| Tenseur | lie_derive (const Tenseur &, const Tenseur &, const Metrique *) |
Lie Derivative of t with respect to x . More... | |
Detailed Description
Tensor handling *** DEPRECATED : use class Tensor instead ***.
()
This class is intended to store the components of a tensorial field in a specific basis. Tensor densities can also be stored. A tensor density 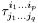 is defined by:
is defined by: 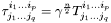 where T is a q -covariant p -contravariant tensor and
where T is a q -covariant p -contravariant tensor and  is the determinant of the used 3-metric. n is called the weight of the tensor density.
is the determinant of the used 3-metric. n is called the weight of the tensor density.
All this is 3D meaning that the indices go from 0 to 2. Moreover, the components are described in orthonormal bases.
When first constructed, the memory for each component is not allocated.
Constructor & Destructor Documentation
◆ Tenseur() [1/11]
|
explicit |
◆ Tenseur() [2/11]
|
explicit |
Constructor for a scalar field and from a Cmp .
Definition at line 240 of file tenseur.C.
References Lorene::Cmp::get_etat().
◆ Tenseur() [3/11]
| Lorene::Tenseur::Tenseur | ( | const Map & | map, |
| int | val, | ||
| const Itbl & | tipe, | ||
| const Base_vect & | triad_i, | ||
| const Metrique * | met = 0x0, |
||
| double | weight = 0 |
||
| ) |
Standard constructor.
- Parameters
-
map the mapping val valence of the tensor tipe 1-D Itblof sizevalencecontaining the type of each index,COVfor a covariant one andCONfor a contravariant one, with the following storage convention:tipe(0): type of the first indextipe(1): type of the second index- and so on...
triad_i vectorial basis (triad) with respect to which the tensor components are defined met for tensor densities only: a pointer on the metric defining the conformal factor weight for tensor densities: the weight
◆ Tenseur() [4/11]
| Lorene::Tenseur::Tenseur | ( | const Map & | map, |
| int | val, | ||
| const Itbl & | tipe, | ||
| const Base_vect * | triad_i, | ||
| const Metrique * | met = 0x0, |
||
| double | weight = 0 |
||
| ) |
Standard constructor with the triad passed as a pointer.
- Parameters
-
map the mapping val valence of the tensor tipe 1-D Itblof sizevalencecontaining the type of each index,COVfor a covariant one andCONfor a contravariant one, with the following storage convention:tipe(0): type of the first indextipe(1): type of the second index- and so on...
triad_i pointer on the vectorial basis (triad) with respect to which the tensor components are defined (can be set to 0x0 for a scalar field) met for tensor densities only: a pointer on the metric defining the conformal factor weight for tensor densities: the weight
◆ Tenseur() [5/11]
| Lorene::Tenseur::Tenseur | ( | const Map & | map, |
| int | val, | ||
| int | tipe, | ||
| const Base_vect & | triad_i, | ||
| const Metrique * | met = 0x0, |
||
| double | weight = 0 |
||
| ) |
Standard constructor when all the indices are of the same type.
- Parameters
-
map the mapping val valence of the tensor tipe the type of the indices. triad_i vectorial basis (triad) with respect to which the tensor components are defined. met for tensor densities only: a pointer on the metric defining the conformal factor weight for tensor densities: the weight
◆ Tenseur() [6/11]
| Lorene::Tenseur::Tenseur | ( | const Tenseur & | source | ) |
Copy constructor.
Definition at line 334 of file tenseur.C.
References c, donne_indices(), donne_place(), met_depend, n_comp, new_der_met(), p_carre_scal, p_derive_con, p_derive_cov, p_gradient, p_gradient_spher, Lorene::pow(), set_dependance(), Tenseur(), and valence.
◆ Tenseur() [7/11]
|
explicit |
Constructor from a symmetric tensor.
Definition at line 382 of file tenseur.C.
References c, donne_indices(), Lorene::Tenseur_sym::donne_place(), met_depend, n_comp, new_der_met(), p_carre_scal, p_derive_con, p_derive_cov, p_gradient, Lorene::pow(), set_dependance(), Tenseur(), valence, and verif().
◆ Tenseur() [8/11]
| Lorene::Tenseur::Tenseur | ( | const Map & | map, |
| const Base_vect & | triad_i, | ||
| FILE * | fich, | ||
| const Metrique * | met = 0x0 |
||
| ) |
Constructor from a file (see sauve(FILE*) ).
- Parameters
-
map the mapping triad_i vectorial basis (triad) with respect to which the tensor components are defined. It will be checked that it coincides with the basis saved in the file. fich file which has been created by the function sauve(FILE*).met for tensor densities only: a pointer on the metric defining the conformal factor
Definition at line 427 of file tenseur.C.
References Lorene::Base_vect::bvect_from_file(), c, etat, Lorene::fread_be(), n_comp, triad, and valence.
◆ Tenseur() [9/11]
| Lorene::Tenseur::Tenseur | ( | const Map & | map, |
| FILE * | fich, | ||
| const Metrique * | met = 0x0 |
||
| ) |
Constructor from a file for a scalar field (see sauve(FILE*) ).
- Parameters
-
map the mapping fich file which has been created by the function sauve(FILE*).met for tensor densities only: a pointer on the metric defining the conformal factor
Definition at line 464 of file tenseur.C.
References c, etat, Lorene::fread_be(), n_comp, triad, and valence.
◆ Tenseur() [10/11]
|
protected |
Constructor used by the derived classes.
- Parameters
-
map the mapping val valence of the tensor tipe 1-D Itblof sizevalencecontaining the type of each index,COVfor a covariant one andCONfor a contravariant one, with the following storage convention:tipe(0): type of the first indextipe(1): type of the second index- and so on...
n_comp the number of components. triad_i vectorial basis (triad) with respect to which the tensor components are defined met for tensor densities only: a pointer on the metric defining the conformal factor weight for tensor densities: the weight
◆ Tenseur() [11/11]
|
protected |
Constructor used by the derived classes when all the indices are of the same type.
- Parameters
-
map the mapping val valence of the tensor tipe the type of the indices. n_comp the number of components. triad_i vectorial basis (triad) with respect to which the tensor components are defined met for tensor densities only: a pointer on the metric defining the conformal factor weight for tensor densities: the weight
◆ ~Tenseur()
|
virtual |
Destructor.
Definition at line 549 of file tenseur.C.
References c, del_t(), met_depend, p_carre_scal, p_derive_con, and p_derive_cov.
Member Function Documentation
◆ allocate_all()
| void Lorene::Tenseur::allocate_all | ( | ) |
Sets the logical state to ETATQCQ (ordinary state) and performs the memory allocation of all the elements, down to the double arrays of the Tbl s.
This function performs in fact recursive calls to set_etat_qcq() on each element of the chain Tenseur -> Cmp -> Valeur -> Mtbl -> Tbl .
Definition at line 673 of file tenseur.C.
References Lorene::Cmp::allocate_all(), c, n_comp, and set_etat_qcq().
◆ annule() [1/2]
| void Lorene::Tenseur::annule | ( | int | l | ) |
◆ annule() [2/2]
| void Lorene::Tenseur::annule | ( | int | l_min, |
| int | l_max | ||
| ) |
Sets the Tenseur to zero in several domains.
- Parameters
-
l_min [input] The Tenseurwill be set (logically) to zero in the domains whose indices are in the range[l_min,l_max] .l_max [input] see the comments for l_min.Note that \c annule(0,nz-1), where \c nz is the total number
of domains, is equivalent toset_etat_zero().
Definition at line 921 of file tenseur.C.
References etat, Lorene::Map::get_mg(), Lorene::Mg3d::get_nzone(), mp, and set_etat_zero().
◆ carre_scal()
| const Tenseur & Lorene::Tenseur::carre_scal | ( | const Metrique & | metre | ) | const |
Returns the scalar square of *this , with respect to met .
Definition at line 1593 of file tenseur.C.
References fait_carre_scal(), get_place_met(), p_carre_scal, and set_dependance().
◆ change_triad()
| void Lorene::Tenseur::change_triad | ( | const Base_vect & | new_triad | ) |
Sets a new vectorial basis (triad) of decomposition and modifies the components accordingly.
Definition at line 684 of file tenseur.C.
References Lorene::Base_vect::change_basis().
◆ dec2_dzpuis()
| void Lorene::Tenseur::dec2_dzpuis | ( | ) |
◆ dec_dzpuis()
| void Lorene::Tenseur::dec_dzpuis | ( | ) |
◆ del_derive()
|
protected |
Logical destructor of all the derivatives.
Definition at line 589 of file tenseur.C.
References del_derive_met(), p_gradient, p_gradient_spher, and set_der_0x0().
◆ del_derive_met()
|
protected |
Logical destructor of the derivatives depending on the i-th element of *met_depend .
Definition at line 570 of file tenseur.C.
References met_depend, p_carre_scal, p_derive_con, p_derive_cov, and set_der_met_0x0().
◆ del_t()
|
protected |
Logical destructor.
Definition at line 561 of file tenseur.C.
References c, del_derive(), and n_comp.
◆ derive_con()
| const Tenseur & Lorene::Tenseur::derive_con | ( | const Metrique & | metre | ) | const |
Returns the contravariant derivative of *this , with respect to met .
Definition at line 1584 of file tenseur.C.
References fait_derive_con(), get_place_met(), p_derive_con, and set_dependance().
◆ derive_cov()
| const Tenseur & Lorene::Tenseur::derive_cov | ( | const Metrique & | met | ) | const |
Returns the covariant derivative of *this , with respect to met .
Definition at line 1570 of file tenseur.C.
References fait_derive_cov(), get_place_met(), gradient(), p_derive_cov, set_dependance(), and valence.
◆ donne_indices()
|
virtual |
Returns the indices of a component given by its position in the Cmp 1-D array c .
- Returns
- 1-D array of integers (
Itbl) of sizevalencegiving the value of each index for the component located at the positionplacein theCmp1-D arrayc. Each element of thisItblis 0, 1 or 2, which corresponds to spatial indices 1, 2 or 3 respectively. If(*this) is a scalar the function returns an undefinedItbl.
Reimplemented in Lorene::Tenseur_sym.
Definition at line 720 of file tenseur.C.
References n_comp, Lorene::Itbl::set(), Lorene::Itbl::set_etat_qcq(), and valence.
◆ donne_place()
|
virtual |
Returns the position in the Cmp 1-D array c of a component given by its indices.
- Returns
- position in the
Cmp1-D arrayc
corresponding to the indices given inidx.idxmust be a 1-DItblof sizevalence, each element of which must be 0, 1 or 2, corresponding to spatial indices 1, 2 or 3 respectively.
Reimplemented in Lorene::Tenseur_sym.
Definition at line 706 of file tenseur.C.
References Lorene::Itbl::get_dim(), Lorene::Itbl::get_ndim(), and valence.
◆ fait_carre_scal()
|
protected |
◆ fait_derive_con()
|
protectedvirtual |
Calculates, if needed, the contravariant derivative of *this , with respect to met .
The result is in *p_derive_con[i]
Reimplemented in Lorene::Tenseur_sym.
Definition at line 1515 of file tenseur.C.
References change_triad(), contract, derive_cov(), gradient(), p_derive_con, Tenseur(), and valence.
◆ fait_derive_cov()
|
protectedvirtual |
Calculates, if needed, the covariant derivative of *this , with respect to met .
The result is in *p_derive_cov[i]
Reimplemented in Lorene::Tenseur_sym.
Definition at line 1445 of file tenseur.C.
References etat.
◆ fait_gradient()
|
protectedvirtual |
Calculates, if needed, the gradient of *this .
The result is in *p_gradient
Reimplemented in Lorene::Tenseur_sym.
Definition at line 1361 of file tenseur.C.
References etat.
◆ fait_gradient_spher()
|
protected |
◆ get_etat()
|
inline |
◆ get_metric()
|
inline |
◆ get_mp()
|
inline |
◆ get_n_comp()
|
inline |
◆ get_place_met()
|
protected |
Returns the position of the pointer on metre in the array met_depend .
Definition at line 614 of file tenseur.C.
References met_depend.
◆ get_poids()
|
inline |
◆ get_triad()
|
inline |
◆ get_type_indice() [1/2]
|
inline |
Returns the type of the index number i .
i must be strictly lower than valence and obey the following convention:
i= 0 : first indexi= 1 : second index- and so on...
- Returns
- COV for a covariant index, CON for a contravariant one.
Definition at line 732 of file tenseur.h.
References type_indice.
◆ get_type_indice() [2/2]
|
inline |
Returns the types of all the indices.
- Returns
- 1-D
Itblof sizevalencecontaining the type of each index,COVfor a covariant one andCON
for a contravariant one.
Definition at line 741 of file tenseur.h.
References type_indice.
◆ get_valence()
|
inline |
◆ gradient()
| const Tenseur & Lorene::Tenseur::gradient | ( | ) | const |
Returns the gradient of *this (Cartesian coordinates)
Definition at line 1558 of file tenseur.C.
References fait_gradient(), and p_gradient.
◆ gradient_spher()
| const Tenseur & Lorene::Tenseur::gradient_spher | ( | ) | const |
Returns the gradient of *this (Spherical coordinates) (scalar field only).
Definition at line 1564 of file tenseur.C.
References fait_gradient_spher(), and p_gradient_spher.
◆ inc2_dzpuis()
| void Lorene::Tenseur::inc2_dzpuis | ( | ) |
◆ inc_dzpuis()
| void Lorene::Tenseur::inc_dzpuis | ( | ) |
◆ inverse_poisson_vect()
| Tenseur Lorene::Tenseur::inverse_poisson_vect | ( | double | lambda | ) | const |
Compute 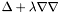 of
of *this , *this being of valence 1.
Definition at line 62 of file tenseur_inv_pois_vect.C.
◆ mult_r_zec()
| void Lorene::Tenseur::mult_r_zec | ( | ) |
◆ new_der_met()
|
protected |
Builds the arrays met_depend , p_derive_cov , p_derive_con and p_carre_scal and fills them with null pointers.
Definition at line 212 of file tenseur.C.
References met_depend, p_carre_scal, p_derive_con, p_derive_cov, and set_der_0x0().
◆ operator()() [1/5]
| const Cmp & Lorene::Tenseur::operator() | ( | ) | const |
◆ operator()() [2/5]
| const Cmp & Lorene::Tenseur::operator() | ( | int | indice | ) | const |
◆ operator()() [3/5]
| const Cmp & Lorene::Tenseur::operator() | ( | int | indice1, |
| int | indice2 | ||
| ) | const |
◆ operator()() [4/5]
| const Cmp & Lorene::Tenseur::operator() | ( | int | indice1, |
| int | indice2, | ||
| int | indice3 | ||
| ) | const |
◆ operator()() [5/5]
Read only in the general case.
Definition at line 1087 of file tenseur.C.
References etat, Lorene::Itbl::get_dim(), Lorene::Itbl::get_ndim(), and valence.
◆ operator=() [1/4]
|
virtual |
Assignment to another Tenseur.
Reimplemented in Lorene::Tenseur_sym.
Definition at line 734 of file tenseur.C.
References etat, metric, poids, triad, type_indice, and valence.
◆ operator=() [2/4]
| void Lorene::Tenseur::operator= | ( | const Cmp & | field | ) |
◆ operator=() [3/4]
| void Lorene::Tenseur::operator= | ( | double | x | ) |
Assignment to a double (scalar field only, except for zero)
Definition at line 808 of file tenseur.C.
References c, metric, poids, set_etat_qcq(), set_etat_zero(), and valence.
◆ operator=() [4/4]
| void Lorene::Tenseur::operator= | ( | int | x | ) |
Assignment to a int (scalar field only, except for zero)
Definition at line 823 of file tenseur.C.
References c, metric, poids, set_etat_qcq(), set_etat_zero(), and valence.
◆ poisson_vect() [1/2]
| void Lorene::Tenseur::poisson_vect | ( | double | lambda, |
| Param & | par, | ||
| Tenseur & | shift, | ||
| Tenseur & | vect, | ||
| Tenseur & | scal, | ||
| bool | verbose = true |
||
| ) | const |
Solves the vectorial Poisson equation : 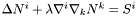 .
.
with 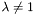 .
.
*this must be given with dzpuis = 4.
It uses the Shibata scheme, where 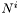 is given by :
is given by :
![\[ N^i = \frac{1}{2}\frac{\lambda+2}{\lambda+1}W^i-\frac{1}{2} \frac{\lambda}{\lambda+1}\left(\nabla^i\chi+\nabla^iW^kx_k\right) \]](form_777.png)
with 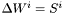 and
and 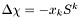 .
.
- Parameters
-
lambda [input] 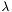 .
. par [input/output] see Map::donne_para_poisson_vect. shift [input] solution 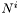 at the previous step. Zero if nothing is known.
at the previous step. Zero if nothing is known. shift [output] solution at this step. vect [input/output] the same thing than for shiftbut for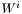 .
. scal [input/output] the same thing than for shiftbut for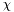 .
. verbose [input] if true, the method gives some info to the standard output.
Definition at line 124 of file tenseur_pde.C.
References etat, get_type_indice(), get_valence(), type_indice, and valence.
◆ poisson_vect() [2/2]
Solves the vectorial Poisson equation 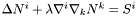 .
.
with 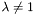 .
.
*this must be given with dzpuis = 4.
It uses the Shibata scheme, where 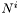 is given by :
is given by :
![\[ N^i = \frac{1}{2}\frac{\lambda+2}{\lambda+1}W^i-\frac{1}{2} \frac{\lambda}{\lambda+1}\left(\nabla^i\chi+\nabla^iW^kx_k\right) \]](form_777.png)
with 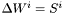 and
and 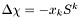 .
.
This version is to be used only with an affine mapping.
- Parameters
-
lambda [input] 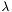 .
. vect [input] 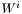 at the previous step. Zero if nothing is known.
at the previous step. Zero if nothing is known. vect [output] 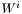 at this step.
at this step. scal [input/output] the same thing than for shiftbut for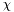 .
.
- Returns
- the solution
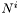 .
.
Definition at line 207 of file tenseur_pde.C.
References metric, mp, poids, poisson_vect(), set_etat_qcq(), triad, type_indice, and valence.
◆ poisson_vect_oohara() [1/2]
| void Lorene::Tenseur::poisson_vect_oohara | ( | double | lambda, |
| Param & | par, | ||
| Tenseur & | shift, | ||
| Tenseur & | scal | ||
| ) | const |
Solves the vectorial Poisson equation 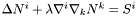 .
.
with 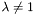 .
.
*this must be given with dzpuis = 3 or 4 and be continuous.
It uses the Oohara scheme, where 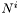 is given by
is given by
![\[ \Delta N^i = S^i-\lambda \nabla^i \chi \]](form_780.png)
with 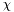 solution of :
solution of :
![\[ \Delta \chi = \frac{1}{\lambda+1}\nabla_k S^k \]](form_781.png)
- Parameters
-
lambda [input] 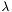 .
. par [input/output] see Map::donne_para_poisson_vect. shift [input] solution 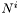 at the previous step. Zero if nothing is known.
at the previous step. Zero if nothing is known. shift [output] solution at this step. scal [input/output] the same thing than for shiftbut for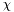 .
.
Definition at line 225 of file tenseur_pde.C.
References etat, get_type_indice(), get_valence(), type_indice, and valence.
◆ poisson_vect_oohara() [2/2]
Solves the vectorial Poisson equation 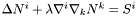 .
.
with 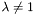 .
.
*this must be given with dzpuis = 3 or 4 and be continuous.
This version is to be used only with an affine mapping.
It uses the Oohara scheme, where 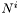 is given by :
is given by :
![\[ \Delta N^i = S^i-\lambda \nabla^i \chi \]](form_780.png)
with 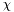 solution of :
solution of :
![\[ \Delta \chi = \frac{1}{\lambda+1}\nabla_k S^k \]](form_781.png)
This version is to be used only with an affine mapping.
- Parameters
-
lambda [input] 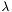 .
. scal [input] 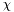 at the previous step. Zero if nothing is known.
at the previous step. Zero if nothing is known. scal [output] 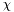 at this step.
at this step.
- Returns
- the solution
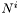 .
.
Definition at line 297 of file tenseur_pde.C.
References metric, mp, poids, poisson_vect_oohara(), set_etat_qcq(), triad, type_indice, and valence.
◆ poisson_vect_regu()
| void Lorene::Tenseur::poisson_vect_regu | ( | int | k_div, |
| int | nzet, | ||
| double | unsgam1, | ||
| double | lambda, | ||
| Param & | par, | ||
| Tenseur & | shift, | ||
| Tenseur & | vect, | ||
| Tenseur & | scal | ||
| ) | const |
Solves the vectorial Poisson equation : 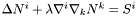 .
.
with 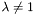 by regularizing the source term.
by regularizing the source term.
*this must be given with dzpuis = 4.
It uses the Shibata scheme, where 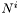 is given by :
is given by :
![\[ N^i = \frac{1}{2}\frac{\lambda+2}{\lambda+1}W^i-\frac{1}{2} \frac{\lambda}{\lambda+1}\left(\nabla^i\chi+\nabla^iW^kx_k\right) \]](form_777.png)
with 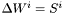 and
and 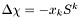 .
.
- Parameters
-
k_div [input] regularization degree. nzet [input] number of domains covering a star. unsgam1 [input] 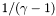 .
. lambda [input] 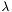 .
. par [input/output] see Map::donne_para_poisson_vect. shift [input] solution 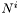 at the previous step. Zero if nothing is known.
at the previous step. Zero if nothing is known. shift [output] solution at this step. vect [input/output] the same thing than for shiftbut for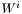 .
. scal [input/output] the same thing than for shiftbut for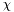 .
.
Definition at line 74 of file tenseur_pde_regu.C.
References etat, get_type_indice(), get_valence(), type_indice, and valence.
◆ sauve()
| void Lorene::Tenseur::sauve | ( | FILE * | fd | ) | const |
Save in a file.
Definition at line 1341 of file tenseur.C.
References etat, Lorene::fwrite_be(), n_comp, Lorene::Base_vect::sauve(), Lorene::Itbl::sauve(), triad, type_indice, and valence.
◆ set() [1/5]
| Cmp & Lorene::Tenseur::set | ( | ) |
Read/write for a scalar (see also operator=(const Cmp&) ).
Definition at line 840 of file tenseur.C.
References del_derive(), and etat.
◆ set() [2/5]
| Cmp & Lorene::Tenseur::set | ( | int | ind | ) |
Read/write for a vector.
Definition at line 850 of file tenseur.C.
References del_derive(), etat, and valence.
◆ set() [3/5]
| Cmp & Lorene::Tenseur::set | ( | int | ind1, |
| int | ind2 | ||
| ) |
Read/write for a tensor of valence 2.
Definition at line 861 of file tenseur.C.
References del_derive(), etat, and valence.
◆ set() [4/5]
| Cmp & Lorene::Tenseur::set | ( | int | ind1, |
| int | ind2, | ||
| int | ind3 | ||
| ) |
Read/write for a tensor of valence 3.
Definition at line 880 of file tenseur.C.
References del_derive(), etat, and valence.
◆ set() [5/5]
Read/write in the general case.
Definition at line 900 of file tenseur.C.
References del_derive(), etat, Lorene::Itbl::get_dim(), Lorene::Itbl::get_ndim(), and valence.
◆ set_dependance()
|
protected |
To be used to describe the fact that the derivatives members have been calculated with met .
First it sets a null element of met_depend to &met and puts this in the list of the dependancies of met .
Definition at line 624 of file tenseur.C.
References met_depend.
◆ set_der_0x0()
|
protected |
Sets the pointers of all the derivatives to zero.
Definition at line 607 of file tenseur.C.
References p_gradient, p_gradient_spher, and set_der_met_0x0().
◆ set_der_met_0x0()
|
protected |
Sets the pointers of the derivatives depending on the i-th element of *met_depend to zero (as well as that i-th element).
Definition at line 599 of file tenseur.C.
References met_depend, p_carre_scal, p_derive_con, and p_derive_cov.
◆ set_etat_nondef()
| void Lorene::Tenseur::set_etat_nondef | ( | ) |
◆ set_etat_qcq()
| void Lorene::Tenseur::set_etat_qcq | ( | ) |
◆ set_etat_zero()
| void Lorene::Tenseur::set_etat_zero | ( | ) |
◆ set_metric()
| void Lorene::Tenseur::set_metric | ( | const Metrique & | met | ) |
◆ set_poids()
| void Lorene::Tenseur::set_poids | ( | double | weight | ) |
◆ set_std_base()
| void Lorene::Tenseur::set_std_base | ( | ) |
◆ set_triad()
| void Lorene::Tenseur::set_triad | ( | const Base_vect & | new_triad | ) |
Assigns a new vectorial basis (triad) of decomposition.
NB: this function modifies only the member triad and leave unchanged the components (member c ). In order to change them coherently with the new basis, the function change_triad(const Base_vect&) must be called instead.
Definition at line 690 of file tenseur.C.
References triad.
◆ verif()
|
protected |
Friends And Related Function Documentation
◆ contract [1/2]
Self contraction of two indices of a Tenseur .
The two indices must be of different type, i.e. covariant and contravariant, or contravariant and covariant.
- Parameters
-
id1 [input] number of the first index for the contraction; id1must be strictly lower than the valence of the tensor and obeys the following convention:id1= 0 : first indexid1= 1 : second index- and so on...
id2 [input] number of the second index for the contraction; id2must be strictly lower than the valence of the tensor and obeys the following convention:id2= 0 : first indexid2= 1 : second index- and so on...
Definition at line 282 of file tenseur_operateur.C.
◆ contract [2/2]
Contraction of two Tenseur .
The two indices must be of different type, i.e. covariant and contravariant, or contravariant and covariant.
- Parameters
-
id1 [input] number of the index of contraction for the first Tenseur;id1must be strictly lower than the valence of the tensor and obeys the following convention:id1= 0 : first indexid1= 1 : second index- and so on...
id2 [input] number of index of contraction for the second one; id2must be strictly lower than the valence of the tensor and obeys the following convention:id2= 0 : first indexid2= 1 : second index- and so on...
Definition at line 351 of file tenseur_operateur.C.
◆ flat_scalar_prod
Scalar product of two Tenseur when the metric is 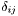 : performs the contraction of the last index of
: performs the contraction of the last index of t1 with the first one of t2 , irrespective of the type of these indices.
Definition at line 656 of file tenseur_operateur.C.
◆ flat_scalar_prod_desal
Same as flat_scalar_prod but with desaliasing.
Definition at line 738 of file tenseur_operateur.C.
◆ lie_derive
Lie Derivative of t with respect to x .
If no other argument is given, it uses partial derivatives with respect to cartesian coordinates to calculate the result (this is the default). Otherwise, it uses the covariant derivative associated to the metric given as last argument.
Definition at line 819 of file tenseur_operateur.C.
◆ manipule [1/2]
Raise or lower the index idx depending on its type, using the given Metrique .
Definition at line 512 of file tenseur_operateur.C.
◆ manipule [2/2]
Raise or lower all the indices, depending on their type, using the given Metrique .
Definition at line 565 of file tenseur_operateur.C.
◆ operator%
Tensorial product with desaliasing.
Definition at line 202 of file tenseur_operateur.C.
◆ operator*
Tensorial product.
Definition at line 122 of file tenseur_operateur.C.
◆ skxk
Contraction of the last index of (*this) with 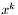 or
or 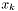 , depending on the type of S .
, depending on the type of S .
The calculation is performed to avoid singularities in the external zone. This is done only for a flat metric.
Definition at line 583 of file tenseur_operateur.C.
Member Data Documentation
◆ c
◆ etat
|
protected |
◆ met_depend
|
protected |
◆ metric
|
protected |
◆ mp
|
protected |
◆ n_comp
|
protected |
◆ p_carre_scal
|
protected |
◆ p_derive_con
|
protected |
◆ p_derive_cov
|
protected |
◆ p_gradient
|
mutableprotected |
◆ p_gradient_spher
|
mutableprotected |
◆ poids
|
protected |
◆ triad
|
protected |
◆ type_indice
|
protected |
◆ valence
The documentation for this class was generated from the following files:
