Divergence-free vectors. More...
#include <vector.h>
Public Member Functions | |
| Vector_divfree (const Map &map, const Base_vect &triad_i, const Metric &met) | |
| Standard constructor. More... | |
| Vector_divfree (const Vector_divfree &) | |
| Copy constructor. More... | |
| Vector_divfree (const Map &map, const Base_vect &triad_i, const Metric &met, FILE *fich) | |
Constructor from a file (see Tensor::sauve(FILE*) ). More... | |
| virtual | ~Vector_divfree () |
| Destructor. More... | |
| void | operator= (const Vector_divfree &a) |
Assignment from another Vector_divfree. More... | |
| virtual void | operator= (const Vector &a) |
Assignment from a Vector. More... | |
| virtual void | operator= (const Tensor &a) |
Assignment from a Tensor. More... | |
| void | set_vr_mu (const Scalar &vr_i, const Scalar &mu_i) |
Sets the angular potentials  (see member (see member p_mu ), and the 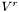 component of the vector. More... component of the vector. More... | |
| void | set_vr_eta_mu (const Scalar &vr_i, const Scalar &eta_i, const Scalar &mu_i) |
Defines the components through 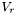 , ,  and and  . More... . More... | |
| void | set_A_mu (const Scalar &A_i, const Scalar &mu_i, const Param *par_bc) |
Defines the components through potentials 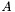 and and  . More... . More... | |
| virtual const Scalar & | eta () const |
Gives the field  such that the angular components such that the angular components 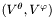 of the vector are written: of the vector are written:
. More... | |
| Vector_divfree | poisson () const |
Computes the solution of a vectorial Poisson equation with *this 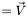 as a source: as a source:
. More... | |
| void | update_etavr () |
Computes the components 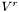 and and  from the potential A and the divergence-free condition, according to : from the potential A and the divergence-free condition, according to :
. More... | |
| Vector_divfree | poisson (Param &par) const |
Computes the solution of a vectorial Poisson equation with *this 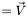 as a source: as a source:
. More... | |
| virtual void | change_triad (const Base_vect &) |
| Sets a new vectorial basis (triad) of decomposition and modifies the components accordingly. More... | |
| void | decompose_div (const Metric &) const |
Makes the Helmholtz decomposition (see documentation of p_potential ) of this with respect to a given Metric , only in the case of contravariant vectors. More... | |
| const Scalar & | potential (const Metric &) const |
| Returns the potential in the Helmholtz decomposition. More... | |
| const Vector_divfree & | div_free (const Metric &) const |
| Returns the div-free vector in the Helmholtz decomposition. More... | |
| virtual void | exponential_filter_r (int lzmin, int lzmax, int p, double alpha=-16.) |
Applies exponential filters to all components (see Scalar::exponential_filter_r ). More... | |
| virtual void | exponential_filter_ylm (int lzmin, int lzmax, int p, double alpha=-16.) |
Applies exponential filters to all components (see Scalar::exponential_filter_ylm ). More... | |
| Scalar & | set (int) |
| Read/write access to a component. More... | |
| Scalar & | set (const Itbl &ind) |
| Returns the value of a component (read/write version). More... | |
| Scalar & | set (int i1, int i2) |
| Returns the value of a component for a tensor of valence 2 (read/write version). More... | |
| Scalar & | set (int i1, int i2, int i3) |
| Returns the value of a component for a tensor of valence 3 (read/write version). More... | |
| Scalar & | set (int i1, int i2, int i3, int i4) |
| Returns the value of a component for a tensor of valence 4 (read/write version). More... | |
| const Scalar & | operator() (int) const |
| Readonly access to a component. More... | |
| const Scalar & | operator() (const Itbl &ind) const |
| Returns the value of a component (read-only version). More... | |
| const Scalar & | operator() (int i1, int i2) const |
| Returns the value of a component for a tensor of valence 2 (read-only version). More... | |
| const Scalar & | operator() (int i1, int i2, int i3) const |
| Returns the value of a component for a tensor of valence 3 (read-only version). More... | |
| const Scalar & | operator() (int i1, int i2, int i3, int i4) const |
| Returns the value of a component for a tensor of valence 4 (read-only version). More... | |
| virtual int | position (const Itbl &idx) const |
Returns the position in the Scalar array cmp of a component given by its index. More... | |
| virtual Itbl | indices (int place) const |
Returns the index of a component given by its position in the Scalar array cmp . More... | |
| virtual void | std_spectral_base () |
| Sets the standard spectal bases of decomposition for each component. More... | |
| virtual void | pseudo_spectral_base () |
| Sets the standard spectal bases of decomposition for each component for a pseudo_vector. More... | |
| virtual const Scalar & | mu () const |
Gives the field  such that the angular components such that the angular components 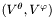 of the vector are written: of the vector are written:
. More... | |
| virtual const Scalar & | A () const |
Gives the field 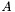 defined by defined by
Related to the curl, A is insensitive to the longitudinal part of the vector. More... | |
| void | update_vtvp () |
Computes the components 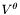 and and 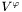 from the potential from the potential  and and  , according to: , according to:
. More... | |
| const Scalar & | divergence (const Metric &) const |
The divergence of this with respect to a Metric . More... | |
| const Vector_divfree | curl () const |
The curl of this with respect to a (flat) Metric . More... | |
| Vector | derive_lie (const Vector &v) const |
Computes the Lie derivative of this with respect to some vector field v. More... | |
| Sym_tensor | ope_killing (const Metric &gam) const |
| Computes the Killing operator associated with a given metric. More... | |
| Sym_tensor | ope_killing_conf (const Metric &gam) const |
| Computes the conformal Killing operator associated with a given metric. More... | |
| Vector | poisson (double lambda, int method=6) const |
Solves the vector Poisson equation with *this as a source. More... | |
| Vector | poisson (double lambda, const Metric_flat &met_f, int method=6) const |
Solves the vector Poisson equation with *this as a source. More... | |
| Vector | poisson (const double lambda, Param &par, int method=6) const |
Solves the vector Poisson equation with *this as a source and parameters controlling the solution. More... | |
| void | poisson_boundary (double lambda, const Mtbl_cf &limit_vr, const Mtbl_cf &limit_eta, const Mtbl_cf &limit_mu, int num_front, double fact_dir, double fact_neu, Vector &resu) const |
Solves the vector Poisson equation with *this as a source with a boundary condition on the excised sphere. More... | |
| void | poisson_boundary2 (double lam, Vector &resu, Scalar boundvr, Scalar boundeta, Scalar boundmu, double dir_vr, double neum_vr, double dir_eta, double neum_eta, double dir_mu, double neum_mu) const |
| Alternative to previous poisson_boundary method for vectors ; this uses method 6 for vectorial solving, updated version (as in the poisson_vector_block routine). More... | |
| Vector | poisson_dirichlet (double lambda, const Valeur &limit_vr, const Valeur &limit_vt, const Valeur &limit_vp, int num_front) const |
| Vector | poisson_neumann (double lambda, const Valeur &limit_vr, const Valeur &limit_vt, const Valeur &limit_vp, int num_front) const |
Solves the vector Poisson equation with *this as a source with a boundary condition on the excised sphere. More... | |
| Vector | poisson_robin (double lambda, const Valeur &limit_vr, const Valeur &limit_vt, const Valeur &limit_vp, double fact_dir, double fact_neu, int num_front) const |
Solves the vector Poisson equation with *this as a source with a boundary condition on the excised sphere. More... | |
| double | flux (double radius, const Metric &met) const |
| Computes the flux of the vector accross a sphere r = const. More... | |
| void | poisson_block (double lambda, Vector &resu) const |
| void | visu_arrows (double xmin, double xmax, double ymin, double ymax, double zmin, double zmax, const char *title0=0x0, const char *filename0=0x0, bool start_dx=true, int nx=8, int ny=8, int nz=8) const |
| 3D visualization via OpenDX. More... | |
| void | visu_streamline (double xmin, double xmax, double ymin, double ymax, double zmin, double zmax, const char *title0=0x0, const char *filename0=0x0, bool start_dx=true, int nx=8, int ny=8, int nz=8) const |
| virtual void | set_etat_nondef () |
Sets the logical state of all components to ETATNONDEF (undefined state). More... | |
| virtual void | set_etat_zero () |
Sets the logical state of all components to ETATZERO (zero state). More... | |
| virtual void | set_etat_qcq () |
Sets the logical state of all components to ETATQCQ (ordinary state). More... | |
| virtual void | allocate_all () |
Performs the memory allocation of all the elements, down to the double arrays of the Tbl s. More... | |
| void | set_triad (const Base_vect &new_triad) |
| Assigns a new vectorial basis (triad) of decomposition. More... | |
| void | annule_domain (int l) |
Sets the Tensor to zero in a given domain. More... | |
| virtual void | annule (int l_min, int l_max) |
Sets the Tensor to zero in several domains. More... | |
| void | annule_extern_cn (int l_0, int deg) |
| Performs a smooth (C^n) transition in a given domain to zero. More... | |
| virtual void | std_spectral_base_odd () |
| Sets the standard odd spectal bases of decomposition for each component. More... | |
| virtual void | dec_dzpuis (int dec=1) |
Decreases by dec units the value of dzpuis and changes accordingly the values in the compactified external domain (CED). More... | |
| virtual void | inc_dzpuis (int inc=1) |
Increases by inc units the value of dzpuis and changes accordingly the values in the compactified external domain (CED). More... | |
| virtual void | exponential_filter_ylm_phi (int lzmin, int lzmax, int p_r, int p_tet, int p_phi, double alpha=-16.) |
Applies exponential filters to all components (see Scalar::exponential_filter_ylm_phi ). More... | |
| void | copy_coefs_from_smaller_grid (const Tensor &tens_small_grid) |
Copies the content of the argument Tensor to this defined on a larger grid, with similar mappings. More... | |
| void | copy_coefs_from_larger_grid (const Tensor &tens_large_grid) |
Copies the content of the argument Tensor to this defined on a smaller grid, with similar mappings. More... | |
| const Tensor & | derive_cov (const Metric &gam) const |
Returns the covariant derivative of this with respect to some metric  . More... . More... | |
| const Tensor & | derive_con (const Metric &gam) const |
Returns the "contravariant" derivative of this with respect to some metric  , by raising the last index of the covariant derivative (cf. More... , by raising the last index of the covariant derivative (cf. More... | |
| Tensor | up (int ind, const Metric &gam) const |
Computes a new tensor by raising an index of *this. More... | |
| Tensor | down (int ind, const Metric &gam) const |
Computes a new tensor by lowering an index of *this. More... | |
| Tensor | up_down (const Metric &gam) const |
Computes a new tensor by raising or lowering all the indices of *this . More... | |
| Tensor | trace (int ind1, int ind2) const |
| Trace on two different type indices. More... | |
| Tensor | trace (int ind1, int ind2, const Metric &gam) const |
| Trace with respect to a given metric. More... | |
| Scalar | trace () const |
| Trace on two different type indices for a valence 2 tensor. More... | |
| Scalar | trace (const Metric &gam) const |
| Trace with respect to a given metric for a valence 2 tensor. More... | |
| const Map & | get_mp () const |
| Returns the mapping. More... | |
| const Base_vect * | get_triad () const |
| Returns the vectorial basis (triad) on which the components are defined. More... | |
| int | get_valence () const |
| Returns the valence. More... | |
| int | get_n_comp () const |
| Returns the number of stored components. More... | |
| int | get_index_type (int i) const |
Gives the type (covariant or contravariant) of the index number i . More... | |
| Itbl | get_index_type () const |
| Returns the types of all the indices. More... | |
| int & | set_index_type (int i) |
Sets the type of the index number i . More... | |
| Itbl & | set_index_type () |
| Sets the types of all the indices. More... | |
| void | operator+= (const Tensor &) |
| += Tensor More... | |
| void | operator-= (const Tensor &) |
| -= Tensor More... | |
| virtual void | sauve (FILE *) const |
| Save in a binary file. More... | |
| virtual void | spectral_display (const char *comment=0x0, double threshold=1.e-7, int precision=4, ostream &ostr=cout) const |
| Displays the spectral coefficients and the associated basis functions of each component. More... | |
Protected Member Functions | |
| virtual void | del_deriv () const |
| Deletes the derived quantities. More... | |
| void | set_der_0x0 () const |
| Sets the pointers on derived quantities to 0x0. More... | |
| void | sol_Dirac_A (const Scalar &aaa, Scalar &eta, Scalar &vr, const Param *par_bc=0x0) const |
| Solves a system of two-coupled first-order PDEs obtained from the divergence-free condition and the requirement that the potential A has a given value. More... | |
| void | sol_Dirac_A_tau (const Scalar &aaa, Scalar &eta, Scalar &vr, const Param *par_bc=0x0) const |
| Solves via a tau method a system of two-coupled first-order PDEs obtained from the divergence-free condition and the requirement that the potential A has a given value. More... | |
| void | sol_Dirac_A_poisson (const Scalar &aaa, Scalar &eta, Scalar &vr, const Param *par_bc=0x0) const |
| Solves via a poisson method a system of two-coupled first-order PDEs obtained from the divergence-free condition and the requirement that the potential A has a given value. More... | |
| void | sol_Dirac_A_1z (const Scalar &aaa, Scalar &eta, Scalar &vr, const Param *par_bc=0x0) const |
| Solves a one-domain system of two-coupled first-order PDEs obtained from the divergence-free condition and the requirement that the potential A has a given value. More... | |
| virtual void | del_derive_met (int) const |
Logical destructor of the derivatives depending on the i-th element of met_depend in the class Vector. More... | |
| void | set_der_met_0x0 (int) const |
Sets all the i-th components of met_depend in the class Vector (p_potential , etc...) to 0x0. More... | |
| void | set_dependance (const Metric &) const |
To be used to describe the fact that the derivatives members have been calculated with met . More... | |
| int | get_place_met (const Metric &) const |
Returns the position of the pointer on metre in the array met_depend . More... | |
| void | compute_derive_lie (const Vector &v, Tensor &resu) const |
Computes the Lie derivative of this with respect to some vector field v (protected method; the public interface is method derive_lie ). More... | |
Protected Attributes | |
| const Metric *const | met_div |
| Metric with respect to which the divergence is defined. More... | |
| Scalar * | p_potential [N_MET_MAX] |
The potential  giving the gradient part in the Helmholtz decomposition of any 3D vector giving the gradient part in the Helmholtz decomposition of any 3D vector 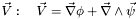 . More... . More... | |
| Vector_divfree * | p_div_free [N_MET_MAX] |
The divergence-free vector 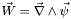 of the Helmholtz decomposition of any 3D vector of the Helmholtz decomposition of any 3D vector 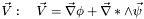 . More... . More... | |
| Scalar * | p_eta |
Field  such that the angular components such that the angular components 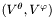 of the vector are written: of the vector are written:
. More... | |
| Scalar * | p_mu |
Field  such that the angular components such that the angular components 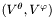 of the vector are written: of the vector are written:
. More... | |
| Scalar * | p_A |
Field 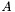 defined by defined by
Insensitive to the longitudinal part of the vector, related to the curl. More... | |
| const Map *const | mp |
| Mapping on which the numerical values at the grid points are defined. More... | |
| int | valence |
| Valence of the tensor (0 = scalar, 1 = vector, etc...) More... | |
| const Base_vect * | triad |
| Vectorial basis (triad) with respect to which the tensor components are defined. More... | |
| Itbl | type_indice |
1D array of integers (class Itbl ) of size valence containing the type of each index: COV for a covariant one and CON for a contravariant one. More... | |
| int | n_comp |
| Number of stored components, depending on the symmetry. More... | |
| Scalar ** | cmp |
Array of size n_comp of pointers onto the components. More... | |
| const Metric * | met_depend [N_MET_MAX] |
Array on the Metric 's which were used to compute derived quantities, like p_derive_cov , etc... More... | |
| Tensor * | p_derive_cov [N_MET_MAX] |
Array of pointers on the covariant derivatives of this with respect to various metrics. More... | |
| Tensor * | p_derive_con [N_MET_MAX] |
Array of pointers on the contravariant derivatives of this with respect to various metrics. More... | |
| Tensor * | p_divergence [N_MET_MAX] |
Array of pointers on the divergence of this with respect to various metrics. More... | |
Detailed Description
Divergence-free vectors.
()
This class is designed to store divergence-free vectors, with the component expressed in a orthonormal spherical basis 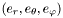 .
.
Constructor & Destructor Documentation
◆ Vector_divfree() [1/3]
| Lorene::Vector_divfree::Vector_divfree | ( | const Map & | map, |
| const Base_vect & | triad_i, | ||
| const Metric & | met | ||
| ) |
Standard constructor.
- Parameters
-
map the mapping triad_i vectorial basis (triad) with respect to which the vector components are defined met the metric with respect to which the divergence is defined
Definition at line 82 of file vector_divfree.C.
References set_der_0x0().
◆ Vector_divfree() [2/3]
| Lorene::Vector_divfree::Vector_divfree | ( | const Vector_divfree & | source | ) |
Copy constructor.
Definition at line 94 of file vector_divfree.C.
References Lorene::Vector::p_eta, Lorene::Vector::p_mu, and set_der_0x0().
◆ Vector_divfree() [3/3]
| Lorene::Vector_divfree::Vector_divfree | ( | const Map & | map, |
| const Base_vect & | triad_i, | ||
| const Metric & | met, | ||
| FILE * | fich | ||
| ) |
Constructor from a file (see Tensor::sauve(FILE*) ).
- Parameters
-
map the mapping triad_i vectorial basis (triad) with respect to which the tensor components are defined. It will be checked that it coincides with the basis saved in the file. met the metric with respect to which the divergence is defined fich file which has been created by the function sauve(FILE*).
Definition at line 106 of file vector_divfree.C.
References set_der_0x0().
◆ ~Vector_divfree()
|
virtual |
Member Function Documentation
◆ A()
|
virtualinherited |
Gives the field 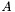 defined by
defined by
![\[ A = {\partial \eta \over \partial r} + { \eta \over r} - {V^r \over r} \]](form_885.png)
Related to the curl, A is insensitive to the longitudinal part of the vector.
Definition at line 138 of file vector_etamu.C.
References Lorene::Tensor::cmp, Lorene::Scalar::div_r_dzpuis(), Lorene::Scalar::dsdr(), Lorene::Vector::eta(), Lorene::Vector::p_A, Lorene::Vector::p_eta, Lorene::Scalar::set_dzpuis(), and Lorene::Tensor::triad.
◆ allocate_all()
|
virtualinherited |
Performs the memory allocation of all the elements, down to the double arrays of the Tbl s.
This function performs in fact recursive calls to set_etat_qcq() on each element of the chain Scalar -> Valeur -> Mtbl -> Tbl .
Reimplemented in Lorene::Scalar.
Definition at line 518 of file tensor.C.
References Lorene::Scalar::allocate_all(), Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), and Lorene::Tensor::n_comp.
◆ annule()
|
virtualinherited |
Sets the Tensor to zero in several domains.
- Parameters
-
l_min [input] The Tensorwill be set (logically) to zero in the domains whose indices are in the range[l_min,l_max] .l_max [input] see the comments for l_min.
Note that annule(0,nz-1) , where nz is the total number of domains, is equivalent to set_etat_zero() .
Reimplemented in Lorene::Scalar.
Definition at line 681 of file tensor.C.
References Lorene::Scalar::annule(), Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), Lorene::Map::get_mg(), Lorene::Mg3d::get_nzone(), Lorene::Tensor::mp, Lorene::Tensor::n_comp, and Lorene::Tensor::set_etat_zero().
◆ annule_domain()
|
inherited |
Sets the Tensor to zero in a given domain.
- Parameters
-
l [input] Index of the domain in which the Tensorwill be set (logically) to zero.
Definition at line 676 of file tensor.C.
References Lorene::Tensor::annule().
◆ annule_extern_cn()
|
inherited |
Performs a smooth (C^n) transition in a given domain to zero.
- Parameters
-
l_0 [input] in the domain of index l0 the tensor is multiplied by the right polynomial (of degree 2n+1), to ensure continuty of the function and its n first derivative at both ends of this domain. The tensor is unchanged in the domains l < l_0 and set to zero in domains l > l_0. deg [input] the degree n of smoothness of the transition.
Definition at line 700 of file tensor.C.
References Lorene::Map::get_mg(), Lorene::Mg3d::get_type_r(), and Lorene::Tensor::mp.
◆ change_triad()
|
virtualinherited |
Sets a new vectorial basis (triad) of decomposition and modifies the components accordingly.
Reimplemented from Lorene::Tensor.
Definition at line 78 of file vector_change_triad.C.
References Lorene::Tensor::cmp, Lorene::Map::comp_p_from_cartesian(), Lorene::Map::comp_r_from_cartesian(), Lorene::Map::comp_t_from_cartesian(), Lorene::Map::comp_x_from_spherical(), Lorene::Map::comp_y_from_spherical(), Lorene::Map::comp_z_from_spherical(), Lorene::Base_vect_cart::get_align(), Lorene::Map::get_bvect_cart(), Lorene::Map::get_bvect_spher(), Lorene::Map::get_mg(), Lorene::Mg3d::get_nt(), Lorene::Mg3d::get_nzone(), Lorene::Tensor::mp, and Lorene::Tensor::triad.
◆ compute_derive_lie()
|
protectedinherited |
Computes the Lie derivative of this with respect to some vector field v (protected method; the public interface is method derive_lie ).
Definition at line 342 of file tensor_calculus.C.
References Lorene::Tensor::cmp, Lorene::contract(), Lorene::Scalar::dec_dzpuis(), Lorene::Tensor::derive_cov(), Lorene::Map::flat_met_cart(), Lorene::Map::flat_met_spher(), Lorene::Scalar::get_dzpuis(), Lorene::Tensor::get_n_comp(), Lorene::Tensor::get_triad(), Lorene::Tensor::indices(), Lorene::Tensor::mp, Lorene::Tensor::n_comp, Lorene::Tensor::operator()(), Lorene::Itbl::set(), Lorene::Tensor::set(), Lorene::Tensor::triad, Lorene::Tensor::type_indice, and Lorene::Tensor::valence.
◆ copy_coefs_from_larger_grid()
|
inherited |
Copies the content of the argument Tensor to this defined on a smaller grid, with similar mappings.
It copies the coefficients, discarding the additional ones. Used for de-aliasing purposes.
- Parameters
-
tens_small_grid [input] Tensorto be copied, defined on the larger grid.
Definition at line 1123 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Scalar::copy_coefs_from_large_grid(), and Lorene::Tensor::n_comp.
◆ copy_coefs_from_smaller_grid()
|
inherited |
Copies the content of the argument Tensor to this defined on a larger grid, with similar mappings.
It copies the coefficients, setting the additional ones to zero. Used for de-aliasing purposes.
- Parameters
-
tens_small_grid [input] Tensorto be copied, defined on the smaller grid.
Definition at line 1116 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Scalar::copy_coefs_from_small_grid(), and Lorene::Tensor::n_comp.
◆ curl()
|
inherited |
The curl of this with respect to a (flat) Metric .
The Vector is assumed to be contravariant.
Definition at line 408 of file vector.C.
References Lorene::Tensor::cmp, Lorene::Scalar::div_r(), Lorene::Scalar::div_tant(), Lorene::Scalar::dsdt(), Lorene::Scalar::dsdx(), Lorene::Scalar::dsdy(), Lorene::Scalar::dsdz(), Lorene::Map::flat_met_cart(), Lorene::Map::flat_met_spher(), Lorene::Map::get_bvect_cart(), Lorene::Map::get_bvect_spher(), Lorene::Base_vect::identify(), Lorene::Tensor::mp, Lorene::Scalar::mult_r(), Lorene::Vector::set(), Lorene::Tensor::set(), Lorene::Scalar::srstdsdp(), and Lorene::Tensor::triad.
◆ dec_dzpuis()
|
virtualinherited |
Decreases by dec units the value of dzpuis and changes accordingly the values in the compactified external domain (CED).
Reimplemented in Lorene::Scalar.
Definition at line 818 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), and Lorene::Tensor::n_comp.
◆ decompose_div()
|
inherited |
Makes the Helmholtz decomposition (see documentation of p_potential ) of this with respect to a given Metric , only in the case of contravariant vectors.
Definition at line 522 of file vector.C.
References Lorene::Scalar::check_dzpuis(), Lorene::Tensor::cmp, Lorene::Vector::divergence(), Lorene::Scalar::get_dzpuis(), Lorene::Scalar::get_etat(), Lorene::Map::get_mg(), Lorene::Mg3d::get_nzone(), Lorene::Tensor::get_place_met(), Lorene::Tensor::mp, Lorene::Vector::p_div_free, Lorene::Vector::p_potential, Lorene::Tensor::set_dependance(), and Lorene::Tensor::type_indice.
◆ del_deriv()
|
protectedvirtual |
Deletes the derived quantities.
Reimplemented from Lorene::Vector.
Definition at line 131 of file vector_divfree.C.
References Lorene::Vector::del_deriv(), and set_der_0x0().
◆ del_derive_met()
|
protectedvirtualinherited |
Logical destructor of the derivatives depending on the i-th element of met_depend in the class Vector.
Reimplemented from Lorene::Tensor.
Definition at line 248 of file vector.C.
References Lorene::Tensor::del_derive_met(), Lorene::Tensor::met_depend, Lorene::Vector::p_div_free, Lorene::Vector::p_potential, and Lorene::Vector::set_der_met_0x0().
◆ derive_con()
Returns the "contravariant" derivative of this with respect to some metric  , by raising the last index of the covariant derivative (cf.
, by raising the last index of the covariant derivative (cf.
method derive_cov() ) with  .
.
Definition at line 1024 of file tensor.C.
References Lorene::Metric::con(), Lorene::contract(), Lorene::Tensor::derive_cov(), Lorene::Tensor::get_index_type(), Lorene::Tensor::get_place_met(), Lorene::Tensor::mp, Lorene::Tensor::p_derive_con, Lorene::Itbl::set(), Lorene::Tensor::set_dependance(), Lorene::Tensor_sym::sym_index1(), Lorene::Tensor_sym::sym_index2(), Lorene::Tensor::Tensor(), Lorene::Tensor::triad, and Lorene::Tensor::valence.
◆ derive_cov()
Returns the covariant derivative of this with respect to some metric  .
.
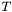 denoting the tensor represented by
denoting the tensor represented by this and 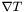 its covariant derivative with respect to the metric
its covariant derivative with respect to the metric  , the extra index (with respect to the indices of
, the extra index (with respect to the indices of 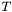 ) of
) of 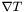 is chosen to be the last one. This convention agrees with that of MTW (see Eq. (10.17) of MTW). For instance, if
is chosen to be the last one. This convention agrees with that of MTW (see Eq. (10.17) of MTW). For instance, if 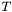 is a 1-form, whose components w.r.t. the triad
is a 1-form, whose components w.r.t. the triad 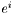 are
are 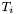 :
: 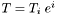 , then the covariant derivative of
, then the covariant derivative of 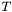 is the bilinear form
is the bilinear form 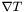 whose components
whose components 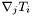 are such that
are such that
![\[ \nabla T = \nabla_j T_i \; e^i \otimes e^j \]](form_177.png)
- Parameters
-
gam metric 
- Returns
- covariant derivative
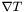 of
of thiswith respect to the connection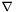 associated with the metric
associated with the metric 
Definition at line 1012 of file tensor.C.
References Lorene::Metric::connect(), Lorene::Tensor::get_place_met(), Lorene::Connection::p_derive_cov(), Lorene::Tensor::p_derive_cov, and Lorene::Tensor::set_dependance().
◆ derive_lie()
Computes the Lie derivative of this with respect to some vector field v.
Definition at line 398 of file vector.C.
References Lorene::Tensor::compute_derive_lie(), Lorene::Tensor::mp, Lorene::Tensor::triad, and Lorene::Tensor::type_indice.
◆ div_free()
|
inherited |
Returns the div-free vector in the Helmholtz decomposition.
It first makes the Helmholtz decomposition (see documentation of p_potential ) of this with respect to a given Metric and then returns 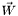 . Only in the case of contravariant vectors.
. Only in the case of contravariant vectors.
Definition at line 510 of file vector.C.
References Lorene::Vector::decompose_div(), Lorene::Tensor::get_place_met(), Lorene::Vector::p_div_free, and Lorene::Tensor::set_dependance().
◆ divergence()
The divergence of this with respect to a Metric .
The Vector is assumed to be contravariant.
Definition at line 387 of file vector.C.
References Lorene::Tensor::divergence().
◆ down()
Computes a new tensor by lowering an index of *this.
- Parameters
-
ind index to be lowered, with the following convention : ind1= 0 : first index of the tensorind1= 1 : second index of the tensor- and so on... (
indmust be of covariant type (CON)).
gam metric used to lower the index (contraction with the twice covariant form of the metric on the index ind).
Definition at line 268 of file tensor_calculus.C.
References Lorene::contract(), Lorene::Metric::cov(), Lorene::Tensor::indices(), Lorene::Tensor::mp, Lorene::Tensor::n_comp, Lorene::Itbl::set(), Lorene::Tensor::set(), Lorene::Tensor::triad, Lorene::Tensor::type_indice, and Lorene::Tensor::valence.
◆ eta()
|
virtual |
Gives the field  such that the angular components
such that the angular components 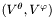 of the vector are written:
of the vector are written:
![\[ V^\theta = {\partial \eta \over \partial\theta} - {1\over\sin\theta} {\partial \mu \over \partial\varphi} \]](form_856.png)
![\[ V^\varphi = {1\over\sin\theta} {\partial \eta \over \partial\varphi} + {\partial \mu \over \partial\theta} \]](form_857.png)
.
Reimplemented from Lorene::Vector.
Definition at line 196 of file vector_divfree.C.
References Lorene::Tensor::cmp, Lorene::Scalar::dsdr(), Lorene::Scalar::get_dzpuis(), Lorene::Scalar::mult_r_dzpuis(), Lorene::Vector::p_eta, Lorene::Scalar::poisson_angu(), and Lorene::Tensor::triad.
◆ exponential_filter_r()
|
virtualinherited |
Applies exponential filters to all components (see Scalar::exponential_filter_r ).
Does a loop for Cartesian components, and works in terms of the r-component,  and
and  for spherical components.
for spherical components.
Reimplemented from Lorene::Tensor.
Definition at line 856 of file vector.C.
References Lorene::Tensor::cmp, Lorene::Vector::eta(), Lorene::Scalar::exponential_filter_r(), Lorene::Map::get_bvect_cart(), Lorene::Map::get_bvect_spher(), Lorene::Base_vect::identify(), Lorene::Tensor::mp, Lorene::Vector::mu(), Lorene::Tensor::n_comp, Lorene::Vector::operator()(), Lorene::Vector::set_vr_eta_mu(), and Lorene::Tensor::triad.
◆ exponential_filter_ylm()
|
virtualinherited |
Applies exponential filters to all components (see Scalar::exponential_filter_ylm ).
Does a loop for Cartesian components, and works in terms of the r-component,  and
and  for spherical components.
for spherical components.
Reimplemented from Lorene::Tensor.
Definition at line 873 of file vector.C.
References Lorene::Tensor::cmp, Lorene::Vector::eta(), Lorene::Scalar::exponential_filter_ylm(), Lorene::Map::get_bvect_cart(), Lorene::Map::get_bvect_spher(), Lorene::Base_vect::identify(), Lorene::Tensor::mp, Lorene::Vector::mu(), Lorene::Tensor::n_comp, Lorene::Vector::operator()(), Lorene::Vector::set_vr_eta_mu(), and Lorene::Tensor::triad.
◆ exponential_filter_ylm_phi()
|
virtualinherited |
Applies exponential filters to all components (see Scalar::exponential_filter_ylm_phi ).
Works only for Cartesian components.
Reimplemented in Lorene::Scalar.
Definition at line 1102 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Map::get_bvect_cart(), Lorene::Base_vect::identify(), Lorene::Tensor::mp, Lorene::Tensor::n_comp, and Lorene::Tensor::triad.
◆ flux()
|
inherited |
Computes the flux of the vector accross a sphere r = const.
- Parameters
-
radius radius of the sphere S on which the flux is to be taken; the center of S is assumed to be the center of the mapping (member mp).radiuscan take the value__infinity(to get the flux at spatial infinity).met metric 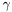 giving the area element of the sphere
giving the area element of the sphere
- Returns
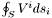 , where
, where 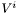 is the vector represented by
is the vector represented by *thisand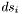 is the area element induced on S by
is the area element induced on S by 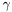 .
.
Definition at line 813 of file vector.C.
References Lorene::Vector::change_triad(), Lorene::Map::get_bvect_spher(), Lorene::Map_af::integrale_surface(), Lorene::Map_af::integrale_surface_infini(), Lorene::Tensor::mp, Lorene::Tensor::triad, Lorene::Tensor::type_indice, and Lorene::Vector::Vector().
◆ get_index_type() [1/2]
|
inlineinherited |
Gives the type (covariant or contravariant) of the index number i .
i must be strictly lower than valence and obey the following convention:
i= 0 : first indexi= 1 : second index- and so on...
- Returns
- COV for a covariant index, CON for a contravariant one.
Definition at line 927 of file tensor.h.
References Lorene::Tensor::type_indice.
◆ get_index_type() [2/2]
|
inlineinherited |
Returns the types of all the indices.
- Returns
- 1-D array of integers (class
Itbl) of sizevalence
containing the type of each index,COVfor a covariant one andCON
for a contravariant one.
Definition at line 937 of file tensor.h.
References Lorene::Tensor::type_indice.
◆ get_mp()
|
inlineinherited |
◆ get_n_comp()
|
inlineinherited |
Returns the number of stored components.
Definition at line 913 of file tensor.h.
References Lorene::Tensor::n_comp.
◆ get_place_met()
|
protectedinherited |
Returns the position of the pointer on metre in the array met_depend .
Definition at line 453 of file tensor.C.
References Lorene::Tensor::met_depend.
◆ get_triad()
|
inlineinherited |
Returns the vectorial basis (triad) on which the components are defined.
Definition at line 907 of file tensor.h.
References Lorene::Tensor::triad.
◆ get_valence()
|
inlineinherited |
◆ inc_dzpuis()
|
virtualinherited |
Increases by inc units the value of dzpuis and changes accordingly the values in the compactified external domain (CED).
Reimplemented in Lorene::Scalar.
Definition at line 826 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), and Lorene::Tensor::n_comp.
◆ indices()
|
inlinevirtualinherited |
Returns the index of a component given by its position in the Scalar array cmp .
- Returns
- the index is stored in an 1-D array (
Itbl) of size 1 giving its value for the component located at the positionplacein theScalararraycmp. The element of thisItbl
corresponds to a spatial index 1, 2 or 3.
Reimplemented from Lorene::Tensor.
◆ mu()
|
virtualinherited |
Gives the field  such that the angular components
such that the angular components 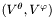 of the vector are written:
of the vector are written:
![\[ V^\theta = {\partial \eta \over \partial\theta} - {1\over\sin\theta} {\partial \mu \over \partial\varphi} \]](form_856.png)
![\[ V^\varphi = {1\over\sin\theta} {\partial \eta \over \partial\varphi} + {\partial \mu \over \partial\theta} \]](form_857.png)
.
Definition at line 107 of file vector_etamu.C.
References Lorene::Tensor::cmp, Lorene::Scalar::div_tant(), Lorene::Scalar::dsdt(), Lorene::Vector::p_mu, Lorene::Scalar::poisson_angu(), Lorene::Scalar::stdsdp(), and Lorene::Tensor::triad.
◆ ope_killing()
|
inherited |
Computes the Killing operator associated with a given metric.
The Killing operator is defined by 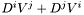 for a contravariant vector and by
for a contravariant vector and by 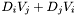 for a covariant vector.
for a covariant vector.
- Parameters
-
gam metric with respect to which the covariant derivative 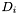 is defined.
is defined.
Definition at line 444 of file vector.C.
References Lorene::Tensor::derive_con(), Lorene::Tensor::derive_cov(), Lorene::Tensor::mp, Lorene::Tensor::set(), Lorene::Tensor::triad, and Lorene::Tensor::type_indice.
◆ ope_killing_conf()
|
inherited |
Computes the conformal Killing operator associated with a given metric.
The conformal Killing operator is defined by 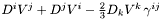 for a contravariant vector and by
for a contravariant vector and by 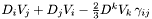 for a covariant vector.
for a covariant vector.
- Parameters
-
gam metric 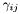 with respect to which the covariant derivative
with respect to which the covariant derivative 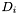 is defined.
is defined.
Definition at line 468 of file vector.C.
References Lorene::Metric::con(), Lorene::Metric::cov(), Lorene::Tensor::derive_con(), Lorene::Tensor::derive_cov(), Lorene::Vector::divergence(), Lorene::Tensor::mp, Lorene::Tensor::set(), Lorene::Tensor::trace(), Lorene::Tensor::triad, and Lorene::Tensor::type_indice.
◆ operator()() [1/5]
|
inherited |
Readonly access to a component.
Definition at line 311 of file vector.C.
References Lorene::Tensor::cmp.
◆ operator()() [2/5]
Returns the value of a component (read-only version).
- Parameters
-
ind 1-D Itblof sizevalencecontaining the values of each index specifing the component, with the following storage convention:ind(0): value of the first index (1, 2 or 3)ind(1): value of the second index (1, 2 or 3)- and so on...
- Returns
- reference on the component specified by
ind
Definition at line 808 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Itbl::get_dim(), Lorene::Itbl::get_ndim(), Lorene::Tensor::position(), and Lorene::Tensor::valence.
◆ operator()() [3/5]
|
inherited |
Returns the value of a component for a tensor of valence 2 (read-only version).
- Parameters
-
i1 value of the first index (1, 2 or 3) i2 value of the second index (1, 2 or 3)
- Returns
- reference on the component specified by
(i1,i2)
Definition at line 770 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::position(), Lorene::Itbl::set(), and Lorene::Tensor::valence.
◆ operator()() [4/5]
|
inherited |
Returns the value of a component for a tensor of valence 3 (read-only version).
- Parameters
-
i1 value of the first index (1, 2 or 3) i2 value of the second index (1, 2 or 3) i3 value of the third index (1, 2 or 3)
- Returns
- reference on the component specified by
(i1,i2,i3)
Definition at line 781 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::position(), Lorene::Itbl::set(), and Lorene::Tensor::valence.
◆ operator()() [5/5]
|
inherited |
Returns the value of a component for a tensor of valence 4 (read-only version).
- Parameters
-
i1 value of the first index (1, 2 or 3) i2 value of the second index (1, 2 or 3) i3 value of the third index (1, 2 or 3) i4 value of the fourth index (1, 2 or 3)
- Returns
- reference on the component specified by
(i1,i2,i3,i4)
Definition at line 793 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::position(), Lorene::Itbl::set(), and Lorene::Tensor::valence.
◆ operator+=()
|
inherited |
+= Tensor
Definition at line 581 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), Lorene::Tensor::indices(), Lorene::Tensor::n_comp, Lorene::Tensor::position(), Lorene::Tensor::triad, Lorene::Tensor::type_indice, and Lorene::Tensor::valence.
◆ operator-=()
|
inherited |
-= Tensor
Definition at line 597 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), Lorene::Tensor::indices(), Lorene::Tensor::n_comp, Lorene::Tensor::position(), Lorene::Tensor::triad, Lorene::Tensor::type_indice, and Lorene::Tensor::valence.
◆ operator=() [1/3]
| void Lorene::Vector_divfree::operator= | ( | const Vector_divfree & | a | ) |
Assignment from another Vector_divfree.
Definition at line 144 of file vector_divfree.C.
References del_deriv(), met_div, and Lorene::Vector::operator=().
◆ operator=() [2/3]
|
virtual |
Assignment from a Vector.
Reimplemented from Lorene::Vector.
Definition at line 156 of file vector_divfree.C.
References del_deriv(), and Lorene::Vector::operator=().
◆ operator=() [3/3]
|
virtual |
Assignment from a Tensor.
Reimplemented from Lorene::Vector.
Definition at line 166 of file vector_divfree.C.
References del_deriv(), and Lorene::Vector::operator=().
◆ poisson() [1/5]
|
inherited |
Solves the vector Poisson equation with *this as a source.
The equation solved is 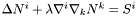 .
. *this must be given with dzpuis = 4. It uses the Helmholtz decomposition (see documentation of p_potential ), with a flat metric, deduced from the triad.
- Parameters
-
lambda [input] 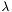 .
. method [input] method used to solve the equation (see Vector::poisson(double, Metric_flat, int) for details).
- Returns
- the solution
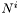 .
.
Definition at line 521 of file vector_poisson.C.
References Lorene::Map::flat_met_cart(), Lorene::Map::flat_met_spher(), Lorene::Tensor::mp, and Lorene::Tensor::triad.
◆ poisson() [2/5]
|
inherited |
Solves the vector Poisson equation with *this as a source.
The equation solved is 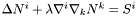 .
. *this must be given with dzpuis = 4. It uses the Helmholtz decomposition (see documentation of p_potential ), with the flat metric met_f given in argument.
- Parameters
-
lambda [input] 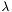 .
. met_f [input] the flat metric for the Helmholtz decomposition. method [input] method used to solve the equation: - 0 : It uses the Helmholtz decomposition (see documentation of
p_potential), with the flat metricmet_fgiven in argument (the default). - 1 : It solves, first for the divergence (calculated using
met_f), then the r -component, the potential, and fianlly the
potential, and fianlly the  potential (see documentation of
potential (see documentation of Vector_div_free. - 2 : The sources is transformed to cartesian components and the equation is solved using Shibata method (see Granclement et al. JCPH 2001.
- 6 : Solves for the r -component and
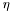 together in a system, and for the
together in a system, and for the 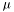 potential (which decouples). The solution is then built from these fields through the method
potential (which decouples). The solution is then built from these fields through the method Vector::set_vr_eta_mu(). It is the default method.
- 0 : It uses the Helmholtz decomposition (see documentation of
- Returns
- the solution
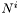 .
.
Definition at line 133 of file vector_poisson.C.
References Lorene::Tensor::cmp.
◆ poisson() [3/5]
Solves the vector Poisson equation with *this as a source and parameters controlling the solution.
The equatiopn solved is 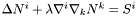 .
. *this must be given with dzpuis = 4. It uses the Helmholtz decomposition (see documentation of p_potential ), with a flat metric, deduced from the triad.
- Parameters
-
lambda [input] 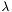 .
. par [input/output] possible parameters uu [input/output] solution u with the boundary condition u =0 at spatial infinity.
Definition at line 546 of file vector_poisson.C.
References Lorene::Param::add_cmp_mod(), Lorene::Param::add_double(), Lorene::Param::add_int(), Lorene::Param::add_int_mod(), Lorene::Cmp::annule_hard(), Lorene::Tensor::cmp, Lorene::Tensor::dec_dzpuis(), Lorene::Scalar::derive_con(), Lorene::Vector::div_free(), Lorene::Map::get_bvect_cart(), Lorene::Map::get_bvect_spher(), Lorene::Param::get_cmp_mod(), Lorene::Param::get_double(), Lorene::Param::get_int(), Lorene::Param::get_int_mod(), Lorene::Scalar::inc_dzpuis(), Lorene::Tensor::mp, poisson(), Lorene::Scalar::poisson(), Lorene::Vector::potential(), Lorene::Vector::set(), Lorene::Tenseur::set(), Lorene::Tenseur::set_etat_qcq(), Lorene::Scalar::set_etat_zero(), Lorene::Tenseur::set_std_base(), and Lorene::Tensor::triad.
◆ poisson() [4/5]
| Vector_divfree Lorene::Vector_divfree::poisson | ( | ) | const |
Computes the solution of a vectorial Poisson equation with *this 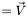 as a source:
as a source:
![\[ \Delta \vec{W} = \vec{V} \]](form_870.png)
.
- Returns
- solution
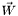 of the above equation with the boundary condition
of the above equation with the boundary condition 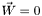 at spatial infinity.
at spatial infinity.
Definition at line 149 of file vector_df_poisson.C.
References Lorene::Tensor::cmp, met_div, Lorene::Tensor::mp, Lorene::Vector::mu(), Lorene::Scalar::poisson(), and Lorene::Tensor::triad.
◆ poisson() [5/5]
| Vector_divfree Lorene::Vector_divfree::poisson | ( | Param & | par | ) | const |
Computes the solution of a vectorial Poisson equation with *this 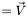 as a source:
as a source:
![\[ \Delta \vec{W} = \vec{V} \]](form_870.png)
.
- Returns
- solution
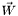 of the above equation with the boundary condition
of the above equation with the boundary condition 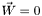 at spatial infinity.
at spatial infinity.
Definition at line 72 of file vector_df_poisson.C.
References Lorene::Param::add_cmp_mod(), Lorene::Param::add_double(), Lorene::Param::add_int(), Lorene::Param::add_int_mod(), Lorene::Tensor::cmp, Lorene::Scalar::div_r(), Lorene::Param::get_cmp_mod(), Lorene::Param::get_double(), Lorene::Param::get_int(), Lorene::Param::get_int_mod(), met_div, Lorene::Tensor::mp, Lorene::Vector::mu(), Lorene::Scalar::mult_r(), Lorene::Scalar::poisson(), Lorene::Scalar::set_etat_zero(), set_vr_mu(), and Lorene::Tensor::triad.
◆ poisson_boundary()
|
inherited |
Solves the vector Poisson equation with *this as a source with a boundary condition on the excised sphere.
The equation solved is 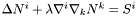 .
. *this must be given with dzpuis = 4. It uses the Helmholtz decomposition (see documentation of p_potential )
- Parameters
-
lambda [input] 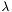 .
. resu [output] the solution 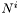 .
.
Definition at line 68 of file vector_poisson_boundary.C.
References Lorene::Tensor::cmp, Lorene::Map::get_mg(), Lorene::Mg3d::get_nzone(), Lorene::Mg3d::get_type_r(), Lorene::Tensor::mp, and Lorene::Tensor::triad.
◆ poisson_boundary2()
|
inherited |
Alternative to previous poisson_boundary method for vectors ; this uses method 6 for vectorial solving, updated version (as in the poisson_vector_block routine).
Boundary arguments are here required as scalar fields.
Definition at line 83 of file vector_poisson_boundary2.C.
References Lorene::Valeur::c_cf, Lorene::Tensor::cmp, Lorene::Map::get_mg(), Lorene::Mg3d::get_nzone(), Lorene::Scalar::get_spectral_va(), Lorene::Mg3d::get_type_r(), Lorene::Tensor::mp, Lorene::Scalar::set_spectral_va(), Lorene::Tensor::triad, and Lorene::Valeur::ylm().
◆ poisson_neumann()
|
inherited |
Solves the vector Poisson equation with *this as a source with a boundary condition on the excised sphere.
The equation solved is 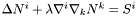 .
. *this must be given with dzpuis = 4. It uses the Helmholtz decomposition (see documentation of p_potential )
- Parameters
-
lambda [input] 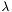 .
. resu [output] the solution 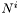 .
.
Definition at line 694 of file vector_poisson_boundary.C.
References Lorene::Tensor::mp, Lorene::Vector::poisson_robin(), and Lorene::Tensor::triad.
◆ poisson_robin()
|
inherited |
Solves the vector Poisson equation with *this as a source with a boundary condition on the excised sphere.
The equation solved is 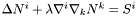 .
. *this must be given with dzpuis = 4. It uses the Helmholtz decomposition (see documentation of p_potential )
- Parameters
-
lambda [input] 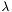 .
. resu [output] the solution 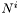 .
.
Definition at line 705 of file vector_poisson_boundary.C.
References Lorene::Scalar::annule_hard(), Lorene::Valeur::base, Lorene::Valeur::c_cf, Lorene::Tensor::cmp, Lorene::Valeur::coef(), Lorene::Scalar::div_tant(), Lorene::Scalar::dsdt(), Lorene::Valeur::get_mg(), Lorene::Map::get_mg(), Lorene::Mg3d::get_np(), Lorene::Mg3d::get_nt(), Lorene::Mg3d::get_nzone(), Lorene::Tensor::mp, Lorene::norme(), Lorene::Scalar::poisson_angu(), Lorene::Valeur::set(), Lorene::Valeur::set_base(), Lorene::Scalar::set_grid_point(), Lorene::Scalar::set_spectral_va(), Lorene::Scalar::stdsdp(), and Lorene::Valeur::ylm().
◆ position()
|
inlinevirtualinherited |
Returns the position in the Scalar array cmp of a component given by its index.
- Returns
- position in the
Scalararraycmp
corresponding to the index given inidx.idxmust be a 1-DItblof size 1, the element of which must be one of the spatial indices 1, 2 or 3.
Reimplemented from Lorene::Tensor.
Definition at line 392 of file vector.h.
References Lorene::Itbl::get_dim(), and Lorene::Itbl::get_ndim().
◆ potential()
Returns the potential in the Helmholtz decomposition.
It first makes the Helmholtz decomposition (see documentation of p_potential ) of this with respect to a given Metric and then returns  . Only in the case of contravariant vectors.
. Only in the case of contravariant vectors.
Definition at line 498 of file vector.C.
References Lorene::Vector::decompose_div(), Lorene::Tensor::get_place_met(), Lorene::Vector::p_potential, and Lorene::Tensor::set_dependance().
◆ pseudo_spectral_base()
|
virtualinherited |
Sets the standard spectal bases of decomposition for each component for a pseudo_vector.
Definition at line 352 of file vector.C.
References Lorene::Tensor::cmp, Lorene::Map::get_bvect_cart(), Lorene::Map::get_bvect_spher(), Lorene::Map::get_mg(), Lorene::Base_vect::identify(), Lorene::Tensor::mp, Lorene::Mg3d::pseudo_base_vect_cart(), Lorene::Mg3d::pseudo_base_vect_spher(), Lorene::Scalar::set_spectral_base(), and Lorene::Tensor::triad.
◆ sauve()
|
virtualinherited |
Save in a binary file.
Reimplemented in Lorene::Tensor_sym, and Lorene::Scalar.
Definition at line 916 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::fwrite_be(), Lorene::Tensor::n_comp, Lorene::Base_vect::sauve(), Lorene::Itbl::sauve(), Lorene::Tensor::triad, Lorene::Tensor::type_indice, and Lorene::Tensor::valence.
◆ set() [1/5]
|
inherited |
Read/write access to a component.
Definition at line 302 of file vector.C.
References Lorene::Tensor::cmp, and Lorene::Vector::del_deriv().
◆ set() [2/5]
Returns the value of a component (read/write version).
- Parameters
-
ind 1-D Itblof sizevalencecontaining the values of each index specifing the component, with the following storage convention:ind(0): value of the first index (1, 2 or 3)ind(1): value of the second index (1, 2 or 3)- and so on...
- Returns
- modifiable reference on the component specified by
ind
Definition at line 664 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), Lorene::Itbl::get_dim(), Lorene::Itbl::get_ndim(), Lorene::Tensor::position(), and Lorene::Tensor::valence.
◆ set() [3/5]
|
inherited |
Returns the value of a component for a tensor of valence 2 (read/write version).
- Parameters
-
i1 value of the first index (1, 2 or 3) i2 value of the second index (1, 2 or 3)
- Returns
- modifiable reference on the component specified by
(i1,i2)
Definition at line 616 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), Lorene::Tensor::position(), Lorene::Itbl::set(), and Lorene::Tensor::valence.
◆ set() [4/5]
|
inherited |
Returns the value of a component for a tensor of valence 3 (read/write version).
- Parameters
-
i1 value of the first index (1, 2 or 3) i2 value of the second index (1, 2 or 3) i3 value of the third index (1, 2 or 3)
- Returns
- modifiable reference on the component specified by
(i1,i2,i3)
Definition at line 631 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), Lorene::Tensor::position(), Lorene::Itbl::set(), and Lorene::Tensor::valence.
◆ set() [5/5]
|
inherited |
Returns the value of a component for a tensor of valence 4 (read/write version).
- Parameters
-
i1 value of the first index (1, 2 or 3) i2 value of the second index (1, 2 or 3) i3 value of the third index (1, 2 or 3) i4 value of the fourth index (1, 2 or 3)
- Returns
- modifiable reference on the component specified by
(i1,i2,i3,i4)
Definition at line 647 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), Lorene::Tensor::position(), Lorene::Itbl::set(), and Lorene::Tensor::valence.
◆ set_A_mu()
| void Lorene::Vector_divfree::set_A_mu | ( | const Scalar & | A_i, |
| const Scalar & | mu_i, | ||
| const Param * | par_bc | ||
| ) |
Defines the components through potentials 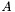 and
and  .
.
(see members p_A and p_mu ),
- Parameters
-
A_i [input] Angular potential 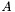
mu_i [input] Angular potential 
Definition at line 123 of file vector_divfree_aux.C.
References Lorene::Tensor::cmp, del_deriv(), Lorene::Tensor::get_mp(), Lorene::Tensor::mp, Lorene::Vector::p_A, Lorene::Vector::p_eta, Lorene::Vector::p_mu, Lorene::Scalar::set_dzpuis(), sol_Dirac_A(), Lorene::Tensor::triad, and Lorene::Vector::update_vtvp().
◆ set_dependance()
|
protectedinherited |
To be used to describe the fact that the derivatives members have been calculated with met .
First it sets a null element of met_depend to &met and puts this in the list of the dependancies of met .
Definition at line 463 of file tensor.C.
References Lorene::Tensor::met_depend, and Lorene::Metric::tensor_depend.
◆ set_der_0x0()
|
protected |
Sets the pointers on derived quantities to 0x0.
Definition at line 138 of file vector_divfree.C.
◆ set_der_met_0x0()
|
protectedinherited |
Sets all the i-th components of met_depend in the class Vector (p_potential , etc...) to 0x0.
Definition at line 264 of file vector.C.
References Lorene::Vector::p_div_free, and Lorene::Vector::p_potential.
◆ set_etat_nondef()
|
virtualinherited |
Sets the logical state of all components to ETATNONDEF
(undefined state).
Reimplemented in Lorene::Scalar.
Definition at line 499 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), Lorene::Tensor::n_comp, and Lorene::Scalar::set_etat_nondef().
◆ set_etat_qcq()
|
virtualinherited |
Sets the logical state of all components to ETATQCQ
(ordinary state).
Reimplemented in Lorene::Scalar.
Definition at line 491 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), Lorene::Tensor::n_comp, and Lorene::Scalar::set_etat_qcq().
◆ set_etat_zero()
|
virtualinherited |
Sets the logical state of all components to ETATZERO
(zero state).
Reimplemented in Lorene::Scalar.
Definition at line 507 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), Lorene::Tensor::n_comp, and Lorene::Scalar::set_etat_zero().
◆ set_index_type() [1/2]
|
inlineinherited |
Sets the type of the index number i .
i must be strictly lower than valence and obey the following convention:
i= 0 : first indexi= 1 : second index- and so on...
- Returns
- reference on the type that can be modified (
COVfor a covariant index,CONfor a contravariant one)
Definition at line 950 of file tensor.h.
References Lorene::Itbl::set(), and Lorene::Tensor::type_indice.
◆ set_index_type() [2/2]
|
inlineinherited |
Sets the types of all the indices.
- Returns
- a reference on the 1-D array of integers (class
Itbl) of sizevalencethat can be modified (COVfor a covariant one andCONfor a contravariant one)
Definition at line 959 of file tensor.h.
References Lorene::Tensor::type_indice.
◆ set_triad()
|
inherited |
Assigns a new vectorial basis (triad) of decomposition.
NB: this function modifies only the member triad and leave unchanged the components (member cmp ). In order to change them coherently with the new basis, the function change_triad(const Base_vect& ) must be called instead.
Definition at line 529 of file tensor.C.
References Lorene::Tensor::triad.
◆ set_vr_eta_mu()
| void Lorene::Vector_divfree::set_vr_eta_mu | ( | const Scalar & | vr_i, |
| const Scalar & | eta_i, | ||
| const Scalar & | mu_i | ||
| ) |
Defines the components through 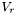 ,
,  and
and  .
.
(see members p_eta and p_mu ),
- Parameters
-
vr_i [input] r-component of the vector eta_i [input] Angular potential 
mu_i [input] Angular potential 
Definition at line 99 of file vector_divfree_aux.C.
References Lorene::Tensor::cmp, Lorene::Tensor::get_mp(), Lorene::Vector::p_eta, Lorene::Vector::p_mu, Lorene::Tensor::triad, and Lorene::Vector::update_vtvp().
◆ set_vr_mu()
Sets the angular potentials  (see member
(see member p_mu ), and the 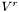 component of the vector.
component of the vector.
The potential  is then deduced from
is then deduced from 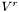 by the divergence-free condition. The components
by the divergence-free condition. The components 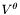 and
and 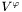 are updated consistently by a call to the method
are updated consistently by a call to the method update_vtvp() .
- Parameters
-
vr_i [input] component 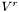 of the vector
of the vector mu_i [input] angular potential 
Definition at line 177 of file vector_divfree.C.
References Lorene::Tensor::cmp, del_deriv(), eta(), Lorene::Vector::p_mu, Lorene::Tensor::triad, and Lorene::Vector::update_vtvp().
◆ sol_Dirac_A()
|
protected |
Solves a system of two-coupled first-order PDEs obtained from the divergence-free condition and the requirement that the potential A has a given value.
The system reads :
![\[ {\partial \eta \over \partial r} + {\eta \over r} - {V^r \over r} = A \]](form_883.png)
![\[ {\partial V^r \over \partial r} + {2 V^r \over r} + {1 \over r}\Delta_{\vartheta \varphi}\eta = 0 \]](form_884.png)
Definition at line 80 of file vector_divfree_A.C.
References Lorene::Map::get_mg(), Lorene::Mg3d::get_type_r(), and Lorene::Tensor::mp.
◆ sol_Dirac_A_1z()
|
protected |
Solves a one-domain system of two-coupled first-order PDEs obtained from the divergence-free condition and the requirement that the potential A has a given value.
The system reads :
![\[ {\partial \eta \over \partial r} + {\eta \over r} - {V^r \over r} = A \]](form_883.png)
![\[ {\partial V^r \over \partial r} + {2 V^r \over r} + {1 \over r}\Delta_{\vartheta \varphi}\eta = 0 \]](form_884.png)
Definition at line 72 of file vector_divfree_A_1z.C.
References Lorene::Map::get_mg(), Lorene::Mg3d::get_type_r(), and Lorene::Tensor::mp.
◆ sol_Dirac_A_poisson()
|
protected |
Solves via a poisson method a system of two-coupled first-order PDEs obtained from the divergence-free condition and the requirement that the potential A has a given value.
The system reads :
![\[ {\partial \eta \over \partial r} + {\eta \over r} - {V^r \over r} = A \]](form_883.png)
![\[ {\partial V^r \over \partial r} + {2 V^r \over r} + {1 \over r}\Delta_{\vartheta \varphi}\eta = 0 \]](form_884.png)
Definition at line 71 of file vector_divfree_A_poisson.C.
References Lorene::Scalar::div_r(), Lorene::Scalar::dsdr(), Lorene::Scalar::lapang(), Lorene::Scalar::mult_r_dzpuis(), and Lorene::Scalar::poisson_tau().
◆ sol_Dirac_A_tau()
|
protected |
Solves via a tau method a system of two-coupled first-order PDEs obtained from the divergence-free condition and the requirement that the potential A has a given value.
The system reads :
![\[ {\partial \eta \over \partial r} + {\eta \over r} - {V^r \over r} = A \]](form_883.png)
![\[ {\partial V^r \over \partial r} + {2 V^r \over r} + {1 \over r}\Delta_{\vartheta \varphi}\eta = 0 \]](form_884.png)
Definition at line 73 of file vector_divfree_A_tau.C.
References Lorene::Map::get_mg(), Lorene::Mg3d::get_type_r(), and Lorene::Tensor::mp.
◆ spectral_display()
|
virtualinherited |
Displays the spectral coefficients and the associated basis functions of each component.
This function shows only the values greater than a given threshold.
- Parameters
-
comment comment to be printed at top of the display (default: 0x0 = nothing printed) threshold [input] Value above which a coefficient is printed (default: 1.e-7) precision [input] Number of printed digits (default: 4) ostr [input] Output stream used for the printing (default: cout)
Reimplemented in Lorene::Scalar.
Definition at line 884 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::indices(), Lorene::Tensor::n_comp, Lorene::Scalar::spectral_display(), and Lorene::Tensor::valence.
◆ std_spectral_base()
|
virtualinherited |
Sets the standard spectal bases of decomposition for each component.
Reimplemented from Lorene::Tensor.
Definition at line 322 of file vector.C.
References Lorene::Tensor::cmp, Lorene::Map::get_bvect_cart(), Lorene::Map::get_bvect_spher(), Lorene::Map::get_mg(), Lorene::Base_vect::identify(), Lorene::Tensor::mp, Lorene::Scalar::set_spectral_base(), Lorene::Mg3d::std_base_vect_cart(), Lorene::Mg3d::std_base_vect_spher(), and Lorene::Tensor::triad.
◆ std_spectral_base_odd()
|
virtualinherited |
Sets the standard odd spectal bases of decomposition for each component.
Currently only implemented for a scalar.
Reimplemented in Lorene::Scalar.
Definition at line 992 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Scalar::std_spectral_base_odd(), and Lorene::Tensor::valence.
◆ trace() [1/4]
|
inherited |
Trace on two different type indices.
- Parameters
-
ind1 first index for the contraction, with the following convention : ind1= 0 : first index of the tensorind1= 1 : second index of the tensor- and so on...
ind2 second index for the contraction
Definition at line 97 of file tensor_calculus.C.
References Lorene::Tensor::cmp, Lorene::Tensor::get_n_comp(), Lorene::Tensor::indices(), Lorene::Tensor::mp, Lorene::Tensor::position(), Lorene::Itbl::set(), Lorene::Tensor::set(), Lorene::Scalar::set_etat_zero(), Lorene::Tensor::triad, Lorene::Tensor::type_indice, and Lorene::Tensor::valence.
◆ trace() [2/4]
Trace with respect to a given metric.
- Parameters
-
ind1 first index for the contraction, with the following convention : ind1= 0 : first index of the tensorind1= 1 : second index of the tensor- and so on...
ind2 second index for the contraction gam metric used to raise or lower ind1 in order that it has a opposite type than ind2
Definition at line 156 of file tensor_calculus.C.
References Lorene::Metric::con(), Lorene::contract(), Lorene::Metric::cov(), Lorene::Tensor::trace(), Lorene::Tensor::type_indice, and Lorene::Tensor::valence.
◆ trace() [3/4]
|
inherited |
Trace on two different type indices for a valence 2 tensor.
Definition at line 183 of file tensor_calculus.C.
References Lorene::Tensor::mp, Lorene::Tensor::operator()(), Lorene::Scalar::set_etat_zero(), Lorene::Tensor::type_indice, and Lorene::Tensor::valence.
◆ trace() [4/4]
Trace with respect to a given metric for a valence 2 tensor.
- Parameters
-
gam metric used to raise or lower one of the indices, in order to take the trace
Definition at line 200 of file tensor_calculus.C.
References Lorene::Metric::con(), Lorene::contract(), Lorene::Metric::cov(), Lorene::Tensor::trace(), Lorene::Tensor::type_indice, and Lorene::Tensor::valence.
◆ up()
Computes a new tensor by raising an index of *this.
- Parameters
-
ind index to be raised, with the following convention : ind1= 0 : first index of the tensorind1= 1 : second index of the tensor- and so on... (
indmust be of covariant type (COV)).
gam metric used to raise the index (contraction with the twice contravariant form of the metric on the index ind).
Definition at line 228 of file tensor_calculus.C.
References Lorene::Metric::con(), Lorene::contract(), Lorene::Tensor::indices(), Lorene::Tensor::mp, Lorene::Tensor::n_comp, Lorene::Itbl::set(), Lorene::Tensor::set(), Lorene::Tensor::triad, Lorene::Tensor::type_indice, and Lorene::Tensor::valence.
◆ up_down()
Computes a new tensor by raising or lowering all the indices of *this .
- Parameters
-
gam metric used to lower the contravariant indices and raising the covariant ones.
Definition at line 308 of file tensor_calculus.C.
References Lorene::Tensor::down(), Lorene::Tensor::Tensor(), Lorene::Tensor::type_indice, Lorene::Tensor::up(), and Lorene::Tensor::valence.
◆ update_etavr()
| void Lorene::Vector_divfree::update_etavr | ( | ) |
Computes the components 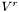 and
and  from the potential A and the divergence-free condition, according to :
from the potential A and the divergence-free condition, according to :
![\[ {\partial \eta \over \ partial r} + { \eta \over r} - {V^r \over r} = A \]](form_881.png)
![\[ {\partial V^r \over \partial r} + {2 V^r \over r} + {1 \over r} \Delta_{\vartheta \varphi} \eta = 0 \]](form_882.png)
.
Definition at line 76 of file vector_divfree_aux.C.
References Lorene::Tensor::cmp, Lorene::Vector::del_deriv(), Lorene::Tensor::mp, Lorene::Vector::p_A, Lorene::Vector::p_eta, and sol_Dirac_A().
◆ update_vtvp()
|
inherited |
Computes the components 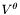 and
and 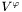 from the potential
from the potential  and
and  , according to:
, according to:
![\[ V^\theta = {\partial \eta \over \partial\theta} - {1\over\sin\theta} {\partial \mu \over \partial\varphi} \]](form_856.png)
![\[ V^\varphi = {1\over\sin\theta} {\partial \eta \over \partial\varphi} + {\partial \mu \over \partial\theta} \]](form_857.png)
.
Definition at line 176 of file vector_etamu.C.
References Lorene::Tensor::cmp, Lorene::Vector::del_deriv(), Lorene::Scalar::dsdt(), Lorene::Vector::p_eta, Lorene::Vector::p_mu, and Lorene::Scalar::stdsdp().
◆ visu_arrows()
|
inherited |
3D visualization via OpenDX.
- Parameters
-
xmin [input] defines with xmaxthe x range of the visualization boxxmax [input] defines with xminthe x range of the visualization boxymin [input] defines with ymaxthe y range of the visualization boxymax [input] defines with yminthe y range of the visualization boxzmin [input] defines with zmaxthe z range of the visualization boxzmax [input] defines with zminthe z range of the visualization boxtitle [input] title for the graph (for OpenDX legend) filename [input] name for the file which will be the input for OpenDX; the default 0x0 is transformed into "vector_arrows" start_dx [input] determines whether OpenDX must be launched (as a subprocess) to view the field; if set to false, only input files for future usage of OpenDX are creatednx [input] number of points in the x direction (uniform sampling)
ny [input] number of points in the y direction (uniform sampling)
nz [input] number of points in the z direction (uniform sampling)
Definition at line 65 of file vector_visu.C.
References Lorene::Valeur::c_cf, Lorene::Vector::change_triad(), Lorene::Scalar::check_dzpuis(), Lorene::Valeur::coef(), Lorene::Map::convert_absolute(), Lorene::Scalar::dec_dzpuis(), Lorene::Map::get_bvect_cart(), Lorene::Map::get_bvect_spher(), Lorene::Scalar::get_dzpuis(), Lorene::Tensor::mp, Lorene::Vector::operator()(), Lorene::Vector::set(), Lorene::Tensor::triad, Lorene::Map::val_lx(), Lorene::Mtbl_cf::val_point(), and Lorene::Vector::Vector().
Member Data Documentation
◆ cmp
|
protectedinherited |
◆ met_depend
|
mutableprotectedinherited |
◆ met_div
|
protected |
◆ mp
|
protectedinherited |
◆ n_comp
|
protectedinherited |
◆ p_A
|
mutableprotectedinherited |
◆ p_derive_con
|
mutableprotectedinherited |
Array of pointers on the contravariant derivatives of this with respect to various metrics.
See the comments of met_depend . See also the comments of method derive_con() for a precise definition of a "contravariant" derivative.
◆ p_derive_cov
|
mutableprotectedinherited |
Array of pointers on the covariant derivatives of this with respect to various metrics.
See the comments of met_depend . See also the comments of method derive_cov() for the index convention of the covariant derivation.
◆ p_div_free
|
mutableprotectedinherited |
◆ p_divergence
|
mutableprotectedinherited |
Array of pointers on the divergence of this with respect to various metrics.
See the comments of met_depend . See also the comments of method divergence() for a precise definition of a the divergence with respect to a given metric.
◆ p_eta
|
mutableprotectedinherited |
◆ p_mu
|
mutableprotectedinherited |
◆ p_potential
|
mutableprotectedinherited |
◆ triad
|
protectedinherited |
◆ type_indice
|
protectedinherited |
◆ valence
|
protectedinherited |
The documentation for this class was generated from the following files:
![\[ A = {\partial \eta \over \ partial r} + { \eta \over r} - {V^r \over r} \]](form_879.png)
