Surface where boundary conditions for quantities in the bulk will be calculated It relies on geometrical properties of the associated Spheroid() (*** WARNING! under development***) More...
#include <excision_surf.h>
Public Member Functions | |
| Excision_surf (const Scalar &h_in, const Metric &gij, const Sym_tensor &Kij2, const Scalar &ppsi, const Scalar &nn, const Vector &beta, double timestep, int int_nos) | |
Constructor of an excision surface embedded in a 3-slice (Time_slice ) of 3+1 formalism. More... | |
| Excision_surf (const Excision_surf &) | |
| Copy constructor. More... | |
| Excision_surf (FILE *) | |
Constructor from a file (see sauve(FILE*) ) More... | |
| virtual | ~Excision_surf () |
| Destructor. More... | |
| void | operator= (const Excision_surf &) |
| Assignment to another Excision_surf. More... | |
| void | get_evol_params_from_ID (double alpha, double beta, double gamma, Scalar &Ee, Vector &Jj, Sym_tensor &Ss) |
| Computes the parameters for the hyperbolic evolution in set_expa_hyperb(), so that the expansion has a C1 matching with initial data. More... | |
| void | set_expa_parab (double c_theta_lap, double c_theta_fin, Scalar &expa_fin) |
| Sets a new value for expansion rescaled over lapse (and its derivative), obtained by parabolic evolution. More... | |
| void | set_expa_hyperb (double alph0, double beta0, double gamma0) |
| Sets a new value for expansion rescaled over lapse (and its derivative), obtained by hyperbolic evolution. More... | |
| const Spheroid & | get_sph () const |
| Returns the spheroid. More... | |
| const Scalar & | get_conf_fact () const |
| Returns the conformal factor associated with the surface. More... | |
| const Scalar & | get_lapse () const |
| Returns the lapse function. More... | |
| const Vector & | get_shift () const |
| Returns the shift vector field. More... | |
| const Metric & | get_gamij () const |
Returns the symmetric tensor 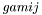 . More... . More... | |
| const Sym_tensor & | get_Kij () const |
returns the 3-d extrinsic curvature 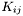 More... More... | |
| double | get_delta_t () const |
| Returns the timestep used for evolution. More... | |
| double | get_no_of_steps () const |
| Returns the internal number of timesteps for one iteration. More... | |
| const Scalar & | get_expa () const |
| Returns the assumed expansion associated to the excised surface at t. More... | |
| const Scalar & | get_dt_expa () const |
| Returns the assumed time derivative of the expansion at t, evolved by functions of this class;. More... | |
| Spheroid & | set_sph () |
| Sets a new spheroid from data. More... | |
| Scalar & | set_conf_fact () |
| Sets the value of the conformal factor. More... | |
| Scalar & | set_lapse () |
| Sets the lapse function. More... | |
| Vector & | set_shift () |
| Sets the shift vector field. More... | |
| Metric & | set_gamij () |
| Sets the 3d metric of the TimeSlice. More... | |
| Sym_tensor & | set_Kij () |
| Sets the extrinsic curvature. More... | |
| double | set_delta_t () |
| double | set_no_of_steps () |
| Scalar & | set_expa () |
| Sets the expansion function on the surface at time t (considering to protect this function) More... | |
| Scalar & | set_dt_expa () |
| Sets the time derivative of the expansion function on the surface at time t (considering to protect this function) More... | |
| const Scalar & | get_BC_conf_fact_1 (bool isMOTS=false) const |
| Source for a Neumann BC on the conformal factor. If boolean isMOTS is false, it is based on expansion value of the spheroid or the value of exppa; it is based on zero expansion if isMOTS is true. More... | |
| const Scalar & | get_BC_lapse_1 (double value) const |
| const Vector & | get_BC_shift_1 (double Omega) const |
| const Scalar & | get_BC_Npsi_1 (double value) const |
| const Scalar & | get_BC_conf_fact_2 (double c_psi_lap, double c_psi_fin, Scalar &expa_fin) const |
| Source for the Dirichlet BC on the conformal factor, based on a parabolic driver for the conformal factor. More... | |
| const Scalar & | get_BC_conf_fact_3 (double c_theta_lap, double c_theta_fin, Scalar &expa_fin) const |
| Source for the Neumann BC on the conformal factor, based on a parabolic driver for the expansio. More... | |
| const Scalar & | get_BC_conf_fact_4 () const |
| Source for the Dirchlet BC on the conformal factor, based on the consistency condition derived from the trace. More... | |
| const Scalar & | get_BC_lapse_2 (double lapse_fin, double c_lapse_lap, double c_lapse_fi) const |
| Source for Dirichlet BC on the lapse, based on a parabolic driver towards arbitrary constant value. More... | |
| const Scalar & | get_BC_lapse_3 (Scalar &dttheta, Scalar &Ee, Vector &Jj, Sym_tensor &Sij, bool sph_sym=true) const |
| Source for Dirichlet BC on the lapse, based on einstein equations. More... | |
| const Scalar & | get_BC_lapse_4 (Scalar &old_nn, Vector &beta_point, Sym_tensor &strain_tens) const |
| Source for Dirichlet BC on the lapse, based on einstein equations (conservation of isotropic gauge) More... | |
| const Scalar & | derive_t_expa (Scalar &Ee, Vector &Jj, Sym_tensor &Sij) const |
| Forms the prospective time derivative for the expansion using projected Einstein equations. Does NOT modify the member dt_expa: do it by hand! More... | |
| const Vector & | get_BC_shift_2 (double c_bb_lap, double c_bb_fin, double c_V_lap, double epsilon) const |
| Source for a Dirichlet BC on the shift, based on a Parabolic driver; no assumptions are made except a global conformal Killing symmetry. More... | |
| const Vector & | get_BC_shift_3 (Scalar &dtpsi, double c_V_lap, double epsilon) const |
| Source for a Dirichlet BC on the shift, based on a Parabolic driver; Radial part is dealt with using a kinematical relation. More... | |
| const Vector & | get_BC_shift_4 (Scalar &dttheta, Scalar &Ee, Vector &Jj, Sym_tensor &Sij, double c_V_lap, double epsilon, bool sph_sym=true) const |
| Source for a Dirichlet BC on the shift, based on a Parabolic driver; Radial part is dealt with using projection of Einstein Equations. More... | |
| const Scalar & | get_BC_Npsi_2 (double value, double c_npsi_lap, double c_npsi_fin) const |
| Source for the Dirichlet BC on (N*Psi1), based on a parabolic driver. More... | |
| const Scalar & | get_BC_Npsi_3 (double n_0, double beta) const |
| Source for the Dirichlet BC on (N*Psi1), with Kerr_Schild-like form for the lapse boundary. More... | |
| const Scalar & | get_BC_Npsi_4 (double Kappa) const |
| Source for a Dirichlet BC on (N*Psi1), fixing a constant surface gravity in space and time. More... | |
| const Scalar & | get_BC_Npsi_5 (double Kappa) const |
| Source for a Neumann BC on (N*Psi1), fixing a constant surface gravity in space and time. More... | |
| virtual void | sauve (FILE *) const |
| Save in a file. More... | |
Protected Member Functions | |
| virtual void | del_deriv () const |
| Deletes all the derived quantities. More... | |
| void | set_der_0x0 () const |
Sets to 0x0 all the pointers on derived quantities. More... | |
Protected Attributes | |
| Spheroid | sph |
| The associated Spheroid object. More... | |
| Scalar | conf_fact |
| The value of the conformal factor on the 3-slice. More... | |
| Scalar | lapse |
| The lapse defined on the 3 slice. More... | |
| Vector | shift |
| The Shift 3-vector on the slice. More... | |
| Metric | gamij |
| The 3-d metric on the slice. More... | |
| Sym_tensor | Kij |
| The 3-d extrinsic curvature on the slice. More... | |
| double | delta_t |
| The time step for evolution in parabolic drivers. More... | |
| double | no_of_steps |
| The internal number of timesteps for one iteration. More... | |
| Scalar | expa |
| The 2d expansion, directly evolved from the initial excision with Einstein Equations. More... | |
| Scalar | dt_expa |
| The time derivative of the expansion, derived from Einstein equations and arbitrary evolution. More... | |
| Scalar * | p_get_BC_conf_fact_1 |
Source of Neumann boundary condition on 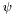 ,. More... ,. More... | |
| Scalar * | p_get_BC_lapse_1 |
Source of Dirichlet boundary condition of 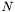 . More... . More... | |
| Vector * | p_get_BC_shift_1 |
Source of Dirichlet BC for the shift vector 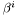 . More... . More... | |
| Scalar * | p_get_BC_Npsi_1 |
Source of Neumann boundary condition on 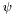 . More... . More... | |
| Scalar * | p_get_BC_conf_fact_2 |
Source of Neumann boundary condition on 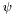 ,. More... ,. More... | |
| Scalar * | p_get_BC_conf_fact_3 |
Source of Neumann boundary condition on 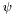 ,. More... ,. More... | |
| Scalar * | p_get_BC_conf_fact_4 |
Source of Birichlet boundary condition on 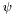 ,. More... ,. More... | |
| Scalar * | p_get_BC_lapse_2 |
Source of Dirichlet boundary condition of 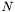 . More... . More... | |
| Scalar * | p_get_BC_lapse_3 |
Source of Dirichlet condtion on 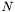 , based on einstein equations. More... , based on einstein equations. More... | |
| Scalar * | p_get_BC_lapse_4 |
Source of Dirichlet condtion on 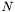 , based on einstein equations (conservation of isotropic gauge) More... , based on einstein equations (conservation of isotropic gauge) More... | |
| Scalar * | p_derive_t_expa |
| Computation of an updated expansion scalar. More... | |
| Vector * | p_get_BC_shift_2 |
Source of Dirichlet BC for the shift vector 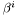 . More... . More... | |
| Vector * | p_get_BC_shift_3 |
Source of Dirichlet BC for the shift vector 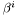 , partly derived from kinematical relation. More... , partly derived from kinematical relation. More... | |
| Vector * | p_get_BC_shift_4 |
Source of Dirichlet BC for the shift vector 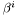 , partly from projection of Einstein Equations. More... , partly from projection of Einstein Equations. More... | |
| Scalar * | p_get_BC_Npsi_2 |
Source of Dirichlet boundary condition on 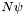 . More... . More... | |
| Scalar * | p_get_BC_Npsi_3 |
Source of Dirichlet boundary condition on 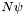 . More... . More... | |
| Scalar * | p_get_BC_Npsi_4 |
Source of Dirichlet boundary condition on 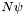 . More... . More... | |
| Scalar * | p_get_BC_Npsi_5 |
Source of Neumann boundary condition on 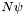 . More... . More... | |
Friends | |
| ostream & | operator<< (ostream &, const Spheroid &) |
| Display. More... | |
Detailed Description
Surface where boundary conditions for quantities in the bulk will be calculated It relies on geometrical properties of the associated Spheroid() (*** WARNING! under development***)
Definition at line 43 of file excision_surf.h.
Constructor & Destructor Documentation
◆ Excision_surf() [1/3]
| Lorene::Excision_surf::Excision_surf | ( | const Scalar & | h_in, |
| const Metric & | gij, | ||
| const Sym_tensor & | Kij2, | ||
| const Scalar & | ppsi, | ||
| const Scalar & | nn, | ||
| const Vector & | beta, | ||
| double | timestep, | ||
| int | int_nos = 1 |
||
| ) |
Constructor of an excision surface embedded in a 3-slice (Time_slice ) of 3+1 formalism.
This is done from the Time_slice data.
- Parameters
-
h_in : the location of the surface r = h_in (WARNING:must be defined on a mono-domain angular grid) gij : the 3-metric on the 3slice Kij : the extrinsic curvature of the 3-slice (covariant representation) timestep : time interval associated with the parabolic-driven boundary conditions. int_nos : Number of iterations to be done during timestep.
Definition at line 64 of file excision_surf.C.
References dt_expa, set_der_0x0(), and Lorene::Scalar::set_etat_zero().
◆ Excision_surf() [2/3]
| Lorene::Excision_surf::Excision_surf | ( | const Excision_surf & | exc_in | ) |
◆ Excision_surf() [3/3]
| Lorene::Excision_surf::Excision_surf | ( | FILE * | ) |
Constructor from a file (see sauve(FILE*) )
◆ ~Excision_surf()
|
virtual |
Member Function Documentation
◆ del_deriv()
|
protectedvirtual |
Deletes all the derived quantities.
Definition at line 139 of file excision_surf.C.
References p_derive_t_expa, p_get_BC_conf_fact_1, p_get_BC_conf_fact_2, p_get_BC_conf_fact_3, p_get_BC_conf_fact_4, p_get_BC_lapse_1, p_get_BC_lapse_2, p_get_BC_lapse_3, p_get_BC_lapse_4, p_get_BC_Npsi_1, p_get_BC_Npsi_2, p_get_BC_Npsi_3, p_get_BC_Npsi_4, p_get_BC_Npsi_5, p_get_BC_shift_1, p_get_BC_shift_2, p_get_BC_shift_3, p_get_BC_shift_4, and set_der_0x0().
◆ derive_t_expa()
| const Scalar & Lorene::Excision_surf::derive_t_expa | ( | Scalar & | Ee, |
| Vector & | Jj, | ||
| Sym_tensor & | Sij | ||
| ) | const |
Forms the prospective time derivative for the expansion using projected Einstein equations. Does NOT modify the member dt_expa: do it by hand!
Definition at line 783 of file excision_surf.C.
References Lorene::Tensor::annule_domain(), Lorene::Scalar::annule_hard(), Lorene::contract(), delta_t, Lorene::Scalar::derive_cov(), Lorene::Spheroid::derive_cov2d(), gamij, Lorene::Spheroid::get_ll(), Lorene::Map::get_mg(), Lorene::Tensor::get_mp(), Lorene::Spheroid::get_qab(), Lorene::Spheroid::get_ricci(), Kij, lapse, p_derive_t_expa, Lorene::Metric::radial_vect(), Lorene::Scalar::set_grid_point(), Lorene::Scalar::set_spectral_va(), Lorene::Spheroid::shear(), shift, sph, Lorene::Scalar::std_spectral_base(), Lorene::Spheroid::theta_minus(), Lorene::Spheroid::theta_plus(), Lorene::Tensor::up_down(), Lorene::Scalar::val_grid_point(), and Lorene::Valeur::ylm().
◆ get_BC_conf_fact_1()
| const Scalar & Lorene::Excision_surf::get_BC_conf_fact_1 | ( | bool | isMOTS = false | ) | const |
Source for a Neumann BC on the conformal factor. If boolean isMOTS is false, it is based on expansion value of the spheroid or the value of exppa; it is based on zero expansion if isMOTS is true.
Definition at line 280 of file excision_surf.C.
References Lorene::Scalar::allocate_all(), Lorene::Tensor::annule_domain(), conf_fact, Lorene::contract(), Lorene::Metric::cov(), Lorene::Scalar::derive_cov(), Lorene::Vector::divergence(), Lorene::Scalar::dsdr(), expa, gamij, Lorene::Valeur::get_etat(), Lorene::Map::get_mg(), Lorene::Tensor::get_mp(), Lorene::Scalar::get_spectral_va(), Kij, lapse, p_get_BC_conf_fact_1, Lorene::pow(), Lorene::Metric::radial_vect(), Lorene::Scalar::set_etat_zero(), Lorene::Scalar::set_spectral_va(), sph, Lorene::Tensor::std_spectral_base(), Lorene::Scalar::std_spectral_base(), Lorene::Spheroid::theta_plus(), Lorene::Tensor::trace(), and Lorene::Valeur::ylm().
◆ get_BC_conf_fact_2()
| const Scalar & Lorene::Excision_surf::get_BC_conf_fact_2 | ( | double | c_psi_lap, |
| double | c_psi_fin, | ||
| Scalar & | expa_fin | ||
| ) | const |
Source for the Dirichlet BC on the conformal factor, based on a parabolic driver for the conformal factor.
Definition at line 364 of file excision_surf.C.
References Lorene::Scalar::allocate_all(), Lorene::Tensor::annule_domain(), conf_fact, Lorene::contract(), Lorene::Metric::cov(), delta_t, Lorene::Scalar::derive_cov(), Lorene::Vector::divergence(), gamij, Lorene::Map::get_mg(), Lorene::Tensor::get_mp(), Kij, lapse, p_get_BC_conf_fact_2, Lorene::pow(), Lorene::Metric::radial_vect(), Lorene::Scalar::set_spectral_va(), sph, Lorene::Tensor::std_spectral_base(), Lorene::Scalar::std_spectral_base(), Lorene::Spheroid::theta_plus(), Lorene::Tensor::trace(), Lorene::Scalar::val_grid_point(), and Lorene::Valeur::ylm().
◆ get_BC_conf_fact_3()
| const Scalar & Lorene::Excision_surf::get_BC_conf_fact_3 | ( | double | c_theta_lap, |
| double | c_theta_fin, | ||
| Scalar & | expa_fin | ||
| ) | const |
Source for the Neumann BC on the conformal factor, based on a parabolic driver for the expansio.
Definition at line 452 of file excision_surf.C.
References Lorene::Scalar::allocate_all(), conf_fact, delta_t, get_BC_conf_fact_1(), Lorene::Map::get_mg(), Lorene::Tensor::get_mp(), Lorene::Scalar::lapang(), lapse, p_get_BC_conf_fact_3, Lorene::pow(), Lorene::Scalar::set_spectral_va(), sph, Lorene::Scalar::std_spectral_base(), Lorene::Spheroid::theta_plus(), Lorene::Scalar::val_grid_point(), and Lorene::Valeur::ylm().
◆ get_BC_conf_fact_4()
| const Scalar & Lorene::Excision_surf::get_BC_conf_fact_4 | ( | ) | const |
Source for the Dirchlet BC on the conformal factor, based on the consistency condition derived from the trace.
Definition at line 533 of file excision_surf.C.
References Lorene::Tensor::annule_domain(), conf_fact, Lorene::contract(), delta_t, Lorene::Scalar::derive_cov(), Lorene::Vector::divergence(), Lorene::Map::flat_met_spher(), gamij, Lorene::Map::get_mg(), Lorene::Tensor::get_mp(), Kij, lapse, p_get_BC_conf_fact_4, Lorene::Scalar::set_spectral_va(), shift, Lorene::Scalar::std_spectral_base(), Lorene::Tensor::trace(), and Lorene::Valeur::ylm().
◆ get_BC_lapse_2()
| const Scalar & Lorene::Excision_surf::get_BC_lapse_2 | ( | double | lapse_fin, |
| double | c_lapse_lap, | ||
| double | c_lapse_fi | ||
| ) | const |
Source for Dirichlet BC on the lapse, based on a parabolic driver towards arbitrary constant value.
Definition at line 603 of file excision_surf.C.
References delta_t, Lorene::Scalar::lapang(), lapse, p_get_BC_lapse_2, Lorene::Scalar::set_spectral_va(), Lorene::Scalar::std_spectral_base(), and Lorene::Valeur::ylm().
◆ get_BC_lapse_3()
| const Scalar & Lorene::Excision_surf::get_BC_lapse_3 | ( | Scalar & | dttheta, |
| Scalar & | Ee, | ||
| Vector & | Jj, | ||
| Sym_tensor & | Sij, | ||
| bool | sph_sym = true |
||
| ) | const |
Source for Dirichlet BC on the lapse, based on einstein equations.
Definition at line 647 of file excision_surf.C.
References Lorene::Scalar::allocate_all(), Lorene::Tensor::annule_domain(), Lorene::Scalar::annule_hard(), Lorene::Valeur::coef_i(), Lorene::Metric::con(), Lorene::Metric_flat::con(), Lorene::contract(), Lorene::Spheroid::delta(), Lorene::Scalar::derive_cov(), Lorene::Spheroid::derive_cov2d(), Lorene::Spheroid::derive_cov2dflat(), Lorene::Map::flat_met_spher(), gamij, Lorene::Spheroid::get_hsurf(), Lorene::Spheroid::get_ll(), Lorene::Map::get_mg(), Lorene::Tensor::get_mp(), Lorene::Spheroid::get_qab(), Lorene::Spheroid::get_ricci(), Kij, lapse, p_get_BC_lapse_3, Lorene::Scalar::poisson_angu(), Lorene::Metric::radial_vect(), Lorene::Tensor::set(), Lorene::Scalar::set_grid_point(), Lorene::Scalar::set_spectral_va(), Lorene::Spheroid::shear(), shift, sph, Lorene::Spheroid::sqrt_q(), Lorene::Tensor::std_spectral_base(), Lorene::Scalar::std_spectral_base(), Lorene::Spheroid::theta_minus(), Lorene::Spheroid::theta_plus(), Lorene::Tensor::up_down(), Lorene::Scalar::val_grid_point(), and Lorene::Valeur::ylm().
◆ get_BC_lapse_4()
| const Scalar & Lorene::Excision_surf::get_BC_lapse_4 | ( | Scalar & | old_nn, |
| Vector & | beta_point, | ||
| Sym_tensor & | strain_tens | ||
| ) | const |
Source for Dirichlet BC on the lapse, based on einstein equations (conservation of isotropic gauge)
Definition at line 15 of file excision_lapse_4.C.
References Lorene::Tensor::annule_domain(), Lorene::Scalar::annule_hard(), Lorene::Metric::con(), conf_fact, Lorene::contract(), delta_t, Lorene::Scalar::derive_con(), Lorene::Tensor::derive_cov(), Lorene::Scalar::derive_cov(), Lorene::Sym_tensor::derive_lie(), Lorene::Scalar::derive_lie(), Lorene::Vector::divergence(), gamij, Lorene::Map::get_bvect_spher(), Lorene::Map::get_mg(), Lorene::Tensor::get_mp(), Lorene::Scalar::inc_dzpuis(), Kij, lapse, Lorene::log(), Lorene::Vector::ope_killing_conf(), p_get_BC_lapse_4, Lorene::Tensor::set(), Lorene::Scalar::set_spectral_va(), shift, Lorene::Tensor::std_spectral_base(), Lorene::Scalar::std_spectral_base(), Lorene::Tensor::trace(), Lorene::Tensor::up_down(), and Lorene::Valeur::ylm().
◆ get_BC_Npsi_2()
| const Scalar & Lorene::Excision_surf::get_BC_Npsi_2 | ( | double | value, |
| double | c_npsi_lap, | ||
| double | c_npsi_fin | ||
| ) | const |
Source for the Dirichlet BC on (N*Psi1), based on a parabolic driver.
Definition at line 1717 of file excision_surf.C.
References conf_fact, delta_t, Lorene::Scalar::lapang(), lapse, p_get_BC_Npsi_2, Lorene::Scalar::set_spectral_va(), Lorene::Scalar::std_spectral_base(), and Lorene::Valeur::ylm().
◆ get_BC_Npsi_3()
| const Scalar & Lorene::Excision_surf::get_BC_Npsi_3 | ( | double | n_0, |
| double | beta | ||
| ) | const |
Source for the Dirichlet BC on (N*Psi1), with Kerr_Schild-like form for the lapse boundary.
Definition at line 1757 of file excision_surf.C.
References conf_fact, Lorene::Map::cost, Lorene::Tensor::get_mp(), lapse, p_get_BC_Npsi_3, Lorene::Scalar::set_spectral_va(), Lorene::sqrt(), and Lorene::Valeur::ylm().
◆ get_BC_Npsi_4()
| const Scalar & Lorene::Excision_surf::get_BC_Npsi_4 | ( | double | Kappa | ) | const |
Source for a Dirichlet BC on (N*Psi1), fixing a constant surface gravity in space and time.
Definition at line 1804 of file excision_surf.C.
References conf_fact, Lorene::contract(), Lorene::Scalar::derive_cov(), gamij, Kij, lapse, p_get_BC_Npsi_4, Lorene::Metric::radial_vect(), Lorene::Scalar::set_dzpuis(), Lorene::Scalar::set_spectral_va(), Lorene::Scalar::std_spectral_base(), and Lorene::Valeur::ylm().
◆ get_BC_Npsi_5()
| const Scalar & Lorene::Excision_surf::get_BC_Npsi_5 | ( | double | Kappa | ) | const |
Source for a Neumann BC on (N*Psi1), fixing a constant surface gravity in space and time.
Definition at line 1825 of file excision_surf.C.
References Lorene::Tensor::annule_domain(), conf_fact, Lorene::contract(), Lorene::Scalar::derive_cov(), gamij, Lorene::Map::get_mg(), Lorene::Tensor::get_mp(), Kij, lapse, p_get_BC_Npsi_5, Lorene::pow(), Lorene::Metric::radial_vect(), Lorene::Scalar::set_spectral_va(), Lorene::Scalar::std_spectral_base(), and Lorene::Valeur::ylm().
◆ get_BC_shift_2()
| const Vector & Lorene::Excision_surf::get_BC_shift_2 | ( | double | c_bb_lap, |
| double | c_bb_fin, | ||
| double | c_V_lap, | ||
| double | epsilon | ||
| ) | const |
Source for a Dirichlet BC on the shift, based on a Parabolic driver; no assumptions are made except a global conformal Killing symmetry.
Definition at line 888 of file excision_surf.C.
References Lorene::Scalar::allocate_all(), Lorene::Tensor::annule_domain(), Lorene::Metric::con(), Lorene::contract(), Lorene::Metric::cov(), delta_t, Lorene::Tensor::derive_cov(), Lorene::Tensor::down(), gamij, Lorene::Map::get_mg(), Lorene::Tensor::get_mp(), Lorene::Spheroid::get_ricci(), Lorene::Scalar::lapang(), lapse, p_get_BC_shift_2, Lorene::Metric::radial_vect(), Lorene::Scalar::set_spectral_va(), shift, sph, Lorene::Vector::std_spectral_base(), Lorene::Tensor::std_spectral_base(), Lorene::Scalar::std_spectral_base(), Lorene::Tensor::up_down(), Lorene::Scalar::val_grid_point(), and Lorene::Valeur::ylm().
◆ get_BC_shift_3()
| const Vector & Lorene::Excision_surf::get_BC_shift_3 | ( | Scalar & | dtpsi, |
| double | c_V_lap, | ||
| double | epsilon | ||
| ) | const |
Source for a Dirichlet BC on the shift, based on a Parabolic driver; Radial part is dealt with using a kinematical relation.
Definition at line 1127 of file excision_surf.C.
References Lorene::Scalar::allocate_all(), Lorene::Tensor::annule_domain(), Lorene::Metric::con(), conf_fact, Lorene::contract(), Lorene::Metric::cov(), delta_t, Lorene::Tensor::derive_cov(), Lorene::Scalar::derive_cov(), Lorene::Vector::divergence(), Lorene::Tensor::down(), Lorene::Map::flat_met_spher(), gamij, Lorene::Map::get_mg(), Lorene::Tensor::get_mp(), Lorene::Spheroid::get_ricci(), lapse, p_get_BC_shift_3, Lorene::Metric::radial_vect(), shift, sph, Lorene::Vector::std_spectral_base(), Lorene::Tensor::std_spectral_base(), Lorene::Tensor::up_down(), and Lorene::Scalar::val_grid_point().
◆ get_BC_shift_4()
| const Vector & Lorene::Excision_surf::get_BC_shift_4 | ( | Scalar & | dttheta, |
| Scalar & | Ee, | ||
| Vector & | Jj, | ||
| Sym_tensor & | Sij, | ||
| double | c_V_lap, | ||
| double | epsilon, | ||
| bool | sph_sym = true |
||
| ) | const |
Source for a Dirichlet BC on the shift, based on a Parabolic driver; Radial part is dealt with using projection of Einstein Equations.
Definition at line 1361 of file excision_surf.C.
References Lorene::Scalar::allocate_all(), Lorene::Tensor::annule_domain(), Lorene::Scalar::annule_hard(), Lorene::Valeur::coef_i(), Lorene::Metric::con(), Lorene::Metric_flat::con(), Lorene::contract(), Lorene::Metric::cov(), Lorene::Spheroid::delta(), delta_t, Lorene::Tensor::derive_cov(), Lorene::Scalar::derive_cov(), Lorene::Spheroid::derive_cov2d(), Lorene::Spheroid::derive_cov2dflat(), Lorene::Tensor::down(), Lorene::Map::flat_met_spher(), gamij, Lorene::Spheroid::get_hsurf(), Lorene::Spheroid::get_ll(), Lorene::Map::get_mg(), Lorene::Tensor::get_mp(), Lorene::Spheroid::get_qab(), Lorene::Spheroid::get_ricci(), Lorene::Scalar::get_spectral_base(), Kij, lapse, p_get_BC_shift_4, Lorene::Metric::radial_vect(), Lorene::Tensor::set(), Lorene::Scalar::set_grid_point(), Lorene::Scalar::set_spectral_va(), Lorene::Spheroid::shear(), shift, sph, Lorene::Spheroid::sqrt_q(), Lorene::Vector::std_spectral_base(), Lorene::Tensor::std_spectral_base(), Lorene::Scalar::std_spectral_base(), Lorene::Spheroid::theta_minus(), Lorene::Spheroid::theta_plus(), Lorene::Tensor::up_down(), Lorene::Scalar::val_grid_point(), and Lorene::Valeur::ylm().
◆ get_conf_fact()
|
inline |
Returns the conformal factor associated with the surface.
Definition at line 170 of file excision_surf.h.
References conf_fact.
◆ get_delta_t()
|
inline |
Returns the timestep used for evolution.
Definition at line 185 of file excision_surf.h.
References delta_t.
◆ get_dt_expa()
|
inline |
Returns the assumed time derivative of the expansion at t, evolved by functions of this class;.
Definition at line 194 of file excision_surf.h.
References dt_expa.
◆ get_evol_params_from_ID()
| void Lorene::Excision_surf::get_evol_params_from_ID | ( | double | alpha, |
| double | beta, | ||
| double | gamma, | ||
| Scalar & | Ee, | ||
| Vector & | Jj, | ||
| Sym_tensor & | Ss | ||
| ) |
Computes the parameters for the hyperbolic evolution in set_expa_hyperb(), so that the expansion has a C1 matching with initial data.
Sets also values for expa() and dt_expa() accordingly with initial conditions
Definition at line 195 of file excision_surf.C.
References Lorene::Valeur::c_cf, derive_t_expa(), Lorene::max(), set_dt_expa(), set_expa(), Lorene::Scalar::set_spectral_va(), sph, Lorene::Scalar::std_spectral_base(), Lorene::Spheroid::theta_plus(), Lorene::Mtbl_cf::val_in_bound_jk(), and Lorene::Valeur::ylm().
◆ get_expa()
|
inline |
Returns the assumed expansion associated to the excised surface at t.
Definition at line 191 of file excision_surf.h.
References expa.
◆ get_gamij()
|
inline |
◆ get_Kij()
|
inline |
◆ get_lapse()
|
inline |
◆ get_no_of_steps()
|
inline |
Returns the internal number of timesteps for one iteration.
Definition at line 188 of file excision_surf.h.
References no_of_steps.
◆ get_shift()
|
inline |
◆ get_sph()
|
inline |
◆ operator=()
| void Lorene::Excision_surf::operator= | ( | const Excision_surf & | surf_in | ) |
Assignment to another Excision_surf.
Definition at line 110 of file excision_surf.C.
References conf_fact, del_deriv(), delta_t, dt_expa, expa, gamij, Kij, lapse, no_of_steps, shift, and sph.
◆ sauve()
|
virtual |
Save in a file.
Definition at line 1851 of file excision_surf.C.
◆ set_conf_fact()
|
inline |
Sets the value of the conformal factor.
Definition at line 200 of file excision_surf.h.
References conf_fact, and del_deriv().
◆ set_der_0x0()
|
protected |
Sets to 0x0 all the pointers on derived quantities.
Definition at line 161 of file excision_surf.C.
References p_derive_t_expa, p_get_BC_conf_fact_1, p_get_BC_conf_fact_2, p_get_BC_conf_fact_3, p_get_BC_conf_fact_4, p_get_BC_lapse_1, p_get_BC_lapse_2, p_get_BC_lapse_3, p_get_BC_lapse_4, p_get_BC_Npsi_1, p_get_BC_Npsi_2, p_get_BC_Npsi_3, p_get_BC_Npsi_4, p_get_BC_Npsi_5, p_get_BC_shift_1, p_get_BC_shift_2, p_get_BC_shift_3, and p_get_BC_shift_4.
◆ set_dt_expa()
|
inline |
Sets the time derivative of the expansion function on the surface at time t (considering to protect this function)
Definition at line 224 of file excision_surf.h.
References del_deriv(), and dt_expa.
◆ set_expa()
|
inline |
Sets the expansion function on the surface at time t (considering to protect this function)
Definition at line 220 of file excision_surf.h.
References del_deriv(), and expa.
◆ set_expa_hyperb()
| void Lorene::Excision_surf::set_expa_hyperb | ( | double | alph0, |
| double | beta0, | ||
| double | gamma0 | ||
| ) |
Sets a new value for expansion rescaled over lapse (and its derivative), obtained by hyperbolic evolution.
Parameters for the hyperbolic driver are determined by the function Excision_surf::get_evol_params_from_ID() so that the expansion stays of regularity $C^{1}$ throughout. All manipulated quantities are 2-dimensional.
Definition at line 99 of file set_expa_evol.C.
References Lorene::Scalar::annule_hard(), delta_t, dt_expa, expa, Lorene::Valeur::get_etat(), Lorene::Map::get_mg(), Lorene::Tensor::get_mp(), Lorene::Scalar::get_spectral_va(), Lorene::Scalar::lapang(), lapse, set_dt_expa(), set_expa(), Lorene::Scalar::set_spectral_va(), Lorene::Scalar::val_grid_point(), and Lorene::Valeur::ylm().
◆ set_expa_parab()
| void Lorene::Excision_surf::set_expa_parab | ( | double | c_theta_lap, |
| double | c_theta_fin, | ||
| Scalar & | expa_fin | ||
| ) |
Sets a new value for expansion rescaled over lapse (and its derivative), obtained by parabolic evolution.
Definition at line 20 of file set_expa_evol.C.
References Lorene::Scalar::annule_hard(), delta_t, expa, Lorene::Valeur::get_etat(), Lorene::Map::get_mg(), Lorene::Tensor::get_mp(), Lorene::Scalar::get_spectral_va(), Lorene::Scalar::lapang(), lapse, set_dt_expa(), set_expa(), Lorene::Scalar::set_spectral_va(), Lorene::Scalar::std_spectral_base(), Lorene::Scalar::val_grid_point(), and Lorene::Valeur::ylm().
◆ set_gamij()
|
inline |
Sets the 3d metric of the TimeSlice.
Definition at line 209 of file excision_surf.h.
References del_deriv(), and gamij.
◆ set_Kij()
|
inline |
Sets the extrinsic curvature.
Definition at line 212 of file excision_surf.h.
References del_deriv(), and Kij.
◆ set_lapse()
|
inline |
Sets the lapse function.
Definition at line 203 of file excision_surf.h.
References del_deriv(), and lapse.
◆ set_shift()
|
inline |
Sets the shift vector field.
Definition at line 206 of file excision_surf.h.
References del_deriv(), and shift.
◆ set_sph()
|
inline |
Sets a new spheroid from data.
Definition at line 197 of file excision_surf.h.
References del_deriv(), and sph.
Friends And Related Function Documentation
◆ operator<<
|
friend |
Display.
Member Data Documentation
◆ conf_fact
|
protected |
The value of the conformal factor on the 3-slice.
Definition at line 53 of file excision_surf.h.
◆ delta_t
|
protected |
The time step for evolution in parabolic drivers.
Definition at line 68 of file excision_surf.h.
◆ dt_expa
|
protected |
The time derivative of the expansion, derived from Einstein equations and arbitrary evolution.
Definition at line 77 of file excision_surf.h.
◆ expa
|
protected |
The 2d expansion, directly evolved from the initial excision with Einstein Equations.
Definition at line 74 of file excision_surf.h.
◆ gamij
|
protected |
The 3-d metric on the slice.
Definition at line 62 of file excision_surf.h.
◆ Kij
|
protected |
The 3-d extrinsic curvature on the slice.
Definition at line 65 of file excision_surf.h.
◆ lapse
|
protected |
The lapse defined on the 3 slice.
Definition at line 56 of file excision_surf.h.
◆ no_of_steps
|
protected |
The internal number of timesteps for one iteration.
Definition at line 71 of file excision_surf.h.
◆ p_derive_t_expa
|
mutableprotected |
Computation of an updated expansion scalar.
Definition at line 94 of file excision_surf.h.
◆ p_get_BC_conf_fact_1
|
mutableprotected |
Source of Neumann boundary condition on 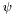 ,.
,.
Definition at line 84 of file excision_surf.h.
◆ p_get_BC_conf_fact_2
|
mutableprotected |
Source of Neumann boundary condition on 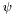 ,.
,.
Definition at line 88 of file excision_surf.h.
◆ p_get_BC_conf_fact_3
|
mutableprotected |
Source of Neumann boundary condition on 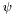 ,.
,.
Definition at line 89 of file excision_surf.h.
◆ p_get_BC_conf_fact_4
|
mutableprotected |
Source of Birichlet boundary condition on 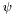 ,.
,.
Definition at line 90 of file excision_surf.h.
◆ p_get_BC_lapse_1
|
mutableprotected |
Source of Dirichlet boundary condition of 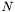 .
.
Definition at line 85 of file excision_surf.h.
◆ p_get_BC_lapse_2
|
mutableprotected |
Source of Dirichlet boundary condition of 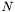 .
.
Definition at line 91 of file excision_surf.h.
◆ p_get_BC_lapse_3
|
mutableprotected |
Source of Dirichlet condtion on 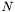 , based on einstein equations.
, based on einstein equations.
Definition at line 92 of file excision_surf.h.
◆ p_get_BC_lapse_4
|
mutableprotected |
Source of Dirichlet condtion on 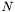 , based on einstein equations (conservation of isotropic gauge)
, based on einstein equations (conservation of isotropic gauge)
Definition at line 93 of file excision_surf.h.
◆ p_get_BC_Npsi_1
|
mutableprotected |
Source of Neumann boundary condition on 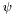 .
.
Definition at line 87 of file excision_surf.h.
◆ p_get_BC_Npsi_2
|
mutableprotected |
Source of Dirichlet boundary condition on 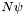 .
.
Definition at line 98 of file excision_surf.h.
◆ p_get_BC_Npsi_3
|
mutableprotected |
Source of Dirichlet boundary condition on 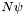 .
.
Definition at line 99 of file excision_surf.h.
◆ p_get_BC_Npsi_4
|
mutableprotected |
Source of Dirichlet boundary condition on 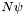 .
.
Definition at line 100 of file excision_surf.h.
◆ p_get_BC_Npsi_5
|
mutableprotected |
Source of Neumann boundary condition on 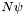 .
.
Definition at line 101 of file excision_surf.h.
◆ p_get_BC_shift_1
|
mutableprotected |
Source of Dirichlet BC for the shift vector 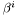 .
.
Definition at line 86 of file excision_surf.h.
◆ p_get_BC_shift_2
|
mutableprotected |
Source of Dirichlet BC for the shift vector 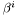 .
.
Definition at line 95 of file excision_surf.h.
◆ p_get_BC_shift_3
|
mutableprotected |
Source of Dirichlet BC for the shift vector 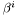 , partly derived from kinematical relation.
, partly derived from kinematical relation.
Definition at line 96 of file excision_surf.h.
◆ p_get_BC_shift_4
|
mutableprotected |
Source of Dirichlet BC for the shift vector 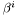 , partly from projection of Einstein Equations.
, partly from projection of Einstein Equations.
Definition at line 97 of file excision_surf.h.
◆ shift
|
protected |
The Shift 3-vector on the slice.
Definition at line 59 of file excision_surf.h.
◆ sph
|
protected |
The associated Spheroid object.
Definition at line 50 of file excision_surf.h.
The documentation for this class was generated from the following files:
