Spheroidal 2-surfaces embedded in a time-slice of the 3+1 formalism. More...
#include <spheroid.h>

Public Member Functions | |
| Spheroid (const Map_af &map, double radius) | |
| The delta tensorial fields linked to Christoffel symbols. More... | |
| Spheroid (const Scalar &h_in, const Metric &gamij, const Sym_tensor &Kij) | |
Constructor of a spheroid embedded in a 3-slice (Time_slice ) of 3+1 formalism. More... | |
| Spheroid (const Spheroid &) | |
| Copy constructor. More... | |
| Spheroid (FILE *) | |
Constructor from a file (see sauve(FILE*) ) More... | |
| virtual | ~Spheroid () |
| Destructor. More... | |
| void | operator= (const Spheroid &) |
| Assignment to another Spheroid. More... | |
| void | set_ephi (const Scalar &) |
| Assigns the conformal Killing vector field to phi. More... | |
| const Scalar & | get_hsurf () const |
Returns the field h_surf. More... | |
| const Metric & | get_qab () const |
Returns the metric 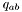 . More... . More... | |
| const Scalar & | get_ricci () const |
Returns the 2-ricci scalar 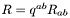 . More... . More... | |
| const Sym_tensor & | get_hh () const |
Returns the symmetric tensor 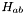 . More... . More... | |
| const Sym_tensor & | get_qq () const |
returns the 3-d degenerate 2-metric 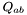 More... More... | |
| const Tensor & | get_proj () const |
returns the 3-d projector on 2-surface 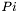 More... More... | |
| const Tensor & | get_jac2d () const |
returns the 2-d jacobian of coordinate transformation 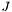 More... More... | |
| const Scalar & | get_trk () const |
Returns the trace K on the 2-surface. More... | |
| const Vector & | get_ll () const |
Returns the vector 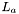 . More... . More... | |
| const Vector & | get_ss () const |
Returns the vector 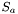 . More... . More... | |
| const Vector & | get_ephi () const |
| Returns the conformal Killing symmetry vector on the 2-surface. More... | |
| const Sym_tensor & | get_jj () const |
Returns the symmetric tensor 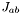 . More... . More... | |
| const Scalar & | get_fff () const |
Returns the normalization scalar F. More... | |
| const Scalar & | get_ggg () const |
Returns the normalization scalar G. More... | |
| bool | get_issphere () const |
| Returns the flag saying whether or not the horizon is geometrically round. More... | |
| Scalar & | set_hsurf () |
Sets the field h_surf. More... | |
| Metric & | set_qab () |
Sets the modified metric (non degenerated) 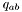 . More... . More... | |
| Scalar & | set_ricci () |
Sets the 2-Ricci scalar 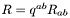 . More... . More... | |
| Sym_tensor & | set_qq () |
Sets the degenerated metric 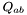 . More... . More... | |
| Tensor & | set_proj () |
Sets the projector 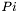 . More... . More... | |
| Sym_tensor & | set_hh () |
Sets the symmetric tensor 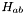 . More... . More... | |
| Scalar & | set_trk () |
Sets the trace K on the 2-surface. More... | |
| Vector & | set_ll () |
Sets the vector 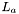 . More... . More... | |
| Vector & | set_ss () |
Sets the vector 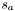 . More... . More... | |
| Sym_tensor & | set_jj () |
Sets the symmetric tensor 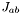 . More... . More... | |
| Scalar & | set_fff () |
Sets the normalization factor F. More... | |
| Scalar & | set_ggg () |
Sets the normalization factor G. More... | |
| bool | set_issphere () |
| Sets the boolean linked to geometrical shape of the horizon. More... | |
| void | update_from_tslice (const Metric &gamij, const Sym_tensor &Kij) |
| Updates from the 3-slice data. More... | |
| const Scalar & | sqrt_q () const |
| Computes the normal vector field to the 2-surface. More... | |
| double | area () const |
| Computes the area of the 2-surface. More... | |
| double | angu_mom () const |
| Computes the angular momentum with respect to a divergence-free vector field tangent to the 2-surface. More... | |
| double | mass () const |
Computes the mass as defined from the calculus of angular momentum, done with respect to a divergence free tangent vector field 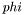 . More... . More... | |
| double | multipole_mass (const int order) const |
| Computes the mass multipole of a given order for the spheroid, assumed to be spherical. More... | |
| double | multipole_angu (const int order) const |
| Computes the angular multipole of a given order for the spheroid, assumed to be spherical. More... | |
| double | epsilon_A_minus_one () const |
| Computation of the refined Penrose parameter for axisymmetric spacetimes, and its difference wrt one. More... | |
| double | epsilon_P_minus_one () const |
| Computation of the classical Penrose parameter, and its difference wrt one. More... | |
| const Scalar & | theta_plus () const |
Computes the outgoing null expansion 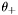 . More... . More... | |
| const Scalar & | theta_minus () const |
Computes the ingoing null expansion 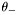 . More... . More... | |
| const Sym_tensor & | shear () const |
Computes the shear of the 2-surface 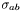 . More... . More... | |
| Tensor | derive_cov2dflat (const Tensor &uu) const |
| Computes the round covariant derivative on the spheroid. More... | |
| const Tensor & | delta () const |
| Computes the delta coefficients for covariant derivative. More... | |
| Tensor | derive_cov2d (const Tensor &uu) const |
| Computes the total covariant derivative on the spheroid. More... | |
| virtual void | sauve (FILE *) const |
| Save in a file. More... | |
Protected Member Functions | |
| virtual void | del_deriv () const |
| Deletes all the derived quantities. More... | |
| void | set_der_0x0 () const |
Sets to 0x0 all the pointers on derived quantities. More... | |
Protected Attributes | |
| Scalar | h_surf |
The location of the 2-surface as r = h_surf 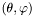 . More... . More... | |
| Tensor | jac2d |
| The jacobian of the adaptation of coordinates (contravariant/covariant representation) More... | |
| Tensor | proj |
| The 3-d projector on the 2-surface (contravariant-covariant form). More... | |
| Sym_tensor | |
| The 3-d covariant degenerated 2-metric on the surface. More... | |
| Vector | ss |
| The adapted normal vector field to spheroid in the 3-slice. More... | |
| Vector | ephi |
The conformal Killing vector field on the 2-surface (set to by default to the axial vector associated with coordinate 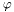 ) More... ) More... | |
| Metric | qab |
| Scalar | ricci |
Induced metric on the 2-surface 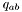 . More... . More... | |
| Sym_tensor | hh |
| The ricci scalar on the 2-surface. More... | |
| Scalar | trk |
| Trace K of the extrinsic curvature of the 3-slice. More... | |
| Vector | ll |
| Normal-tangent component of the extrinsic curvature of the 3-slice. More... | |
| Sym_tensor | jj |
| Tangent components of the extrinsic curvature of the 3-slice. More... | |
| Scalar | fff |
| Normalization function for the outgoing null vector l. More... | |
| Scalar | ggg |
| Normalization function for the ingoing null vector k. More... | |
| Scalar | zeta |
| bool | issphere |
| Flag to know whether the horizon is geometrically round or distorted. More... | |
| Scalar * | p_sqrt_q |
Surface element 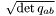 . More... . More... | |
| double * | p_area |
| The area of the 2-surface. More... | |
| double * | p_angu_mom |
| The angular momentum. More... | |
| double * | p_mass |
| Mass defined from angular momentum. More... | |
| double * | p_multipole_mass |
| Mass multipole for the spheroid. More... | |
| double * | p_multipole_angu |
| Angular momentum multipole for the spheroid. More... | |
| double * | p_epsilon_A_minus_one |
| double * | p_epsilon_P_minus_one |
| Refined Penrose parameter, difference wrt one. More... | |
| Scalar * | p_theta_plus |
| Classical Penrose parameter, difference wrt one. More... | |
| Scalar * | p_theta_minus |
| Null ingoing expansion. More... | |
| Sym_tensor * | p_shear |
| The shear tensor. More... | |
| Tensor * | p_delta |
Friends | |
| ostream & | operator<< (ostream &, const Spheroid &) |
| Display. More... | |
Detailed Description
Spheroidal 2-surfaces embedded in a time-slice of the 3+1 formalism.
()
Definition at line 84 of file spheroid.h.
Constructor & Destructor Documentation
◆ Spheroid() [1/4]
| Lorene::Spheroid::Spheroid | ( | const Map_af & | map, |
| double | radius | ||
| ) |
The delta tensorial fields linked to Christoffel symbols.
Standard constructor. The input mapping must be defined on a mono-domain angular grid (see Mg3d::get_angu_mono_domain() for details).
Definition at line 97 of file spheroid.C.
References Lorene::Map::get_mg(), Lorene::Mg3d::get_nr(), Lorene::Mg3d::get_nzone(), and Lorene::Mg3d::get_type_r().
◆ Spheroid() [2/4]
| Lorene::Spheroid::Spheroid | ( | const Scalar & | h_in, |
| const Metric & | gamij, | ||
| const Sym_tensor & | Kij | ||
| ) |
Constructor of a spheroid embedded in a 3-slice (Time_slice ) of 3+1 formalism.
This is done from the Time_slice data.
- Parameters
-
h_in : the location of the surface r = h_in (WARNING:must be defined on a mono-domain angular grid) gamij : the 3-metric on the 3-slice Kij : the extrinsic curvature of the 3-slice (covariant representation)
Definition at line 153 of file spheroid.C.
References Lorene::Scalar::allocate_all(), Lorene::Tensor::allocate_all(), Lorene::Tensor::annule_domain(), Lorene::Scalar::annule_hard(), area(), Lorene::Valeur::c_cf, Lorene::Valeur::coef(), Lorene::Metric::con(), Lorene::contract(), Lorene::Metric::cov(), Lorene::Scalar::dec_dzpuis(), del_deriv(), Lorene::Scalar::derive_con(), Lorene::Scalar::derive_cov(), Lorene::Tensor::down(), ephi, fff, Lorene::Mg3d::get_angu_1dom(), Lorene::Map::get_bvect_spher(), Lorene::Map::get_mg(), Lorene::Metric::get_mp(), Lorene::Tensor::get_mp(), Lorene::Mg3d::get_np(), Lorene::Mg3d::get_nr(), Lorene::Mg3d::get_nt(), Lorene::Mg3d::get_nzone(), Lorene::Scalar::get_spectral_base(), Lorene::Scalar::get_spectral_va(), ggg, Lorene::Base_val::give_quant_numbers(), h_surf, hh, jac2d, jj, ll, Lorene::Scalar::mult_cost(), proj, qq, Lorene::Map::r, ricci, Lorene::Metric::ricci(), Lorene::Itbl::set(), Lorene::Vector::set(), Lorene::Tensor::set(), set_der_0x0(), Lorene::Tensor::set_etat_zero(), Lorene::Scalar::set_grid_point(), Lorene::Tensor::set_index_type(), Lorene::Scalar::set_spectral_va(), Lorene::sqrt(), sqrt_q(), Lorene::Scalar::srdsdt(), Lorene::Scalar::srstdsdp(), ss, Lorene::Vector::std_spectral_base(), Lorene::Tensor::std_spectral_base(), Lorene::Scalar::std_spectral_base(), Lorene::Tensor::trace(), trk, Lorene::Tensor::up(), Lorene::Scalar::val_grid_point(), Lorene::Map_radial::val_lx_jk(), Lorene::Valeur::val_point_jk(), and Lorene::Valeur::ylm().
◆ Spheroid() [3/4]
| Lorene::Spheroid::Spheroid | ( | const Spheroid & | sph_in | ) |
◆ Spheroid() [4/4]
| Lorene::Spheroid::Spheroid | ( | FILE * | ) |
Constructor from a file (see sauve(FILE*) )
◆ ~Spheroid()
|
virtual |
Member Function Documentation
◆ angu_mom()
| double Lorene::Spheroid::angu_mom | ( | ) | const |
Computes the angular momentum with respect to a divergence-free vector field tangent to the 2-surface.
This is defined as
![\[ {\cal J} = \int h^2 L_i \phi^i \sqrt{\det q_{ab}} \sin \theta {\rm d}\theta {\rm d}\varphi \]](form_673.png)
- Parameters
-
phi : the divergence-free vector field 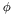
Definition at line 724 of file spheroid.C.
References Lorene::contract(), Lorene::Map::get_bvect_spher(), get_ephi(), Lorene::Tensor::get_mp(), h_surf, Lorene::Map_af::integrale_surface(), jac2d, ll, p_angu_mom, and sqrt_q().
◆ area()
| double Lorene::Spheroid::area | ( | ) | const |
Computes the area of the 2-surface.
This is defined as
![\[ {\cal A} = \int h^2 \sqrt{\det q_{ab}} \sin \theta {\rm d}\theta {\rm d}\varphi \]](form_672.png)
Definition at line 711 of file spheroid.C.
References Lorene::Tensor::get_mp(), h_surf, Lorene::Map_af::integrale_surface(), p_area, and sqrt_q().
◆ del_deriv()
|
protectedvirtual |
Deletes all the derived quantities.
Definition at line 653 of file spheroid.C.
References p_angu_mom, p_area, p_epsilon_P_minus_one, p_mass, p_multipole_angu, p_multipole_mass, p_shear, p_sqrt_q, p_theta_minus, p_theta_plus, and set_der_0x0().
◆ delta()
| const Tensor & Lorene::Spheroid::delta | ( | ) | const |
Computes the delta coefficients for covariant derivative.
Definition at line 1206 of file spheroid.C.
References Lorene::Metric::con(), Lorene::Metric::cov(), derive_cov2dflat(), Lorene::Map::get_bvect_spher(), Lorene::Metric::get_mp(), Lorene::Tensor::set(), and Lorene::Tensor::set_index_type().
◆ derive_cov2d()
Computes the total covariant derivative on the spheroid.
Definition at line 1243 of file spheroid.C.
References Lorene::contract(), delta(), derive_cov2dflat(), Lorene::Tensor::get_index_type(), and Lorene::Tensor::get_valence().
◆ derive_cov2dflat()
Computes the round covariant derivative on the spheroid.
Definition at line 957 of file spheroid.C.
References Lorene::Map::get_bvect_spher(), Lorene::Tensor::get_index_type(), Lorene::Tensor::get_mp(), Lorene::Tensor::get_n_comp(), Lorene::Tensor::get_triad(), Lorene::Tensor::get_valence(), Lorene::Tensor::indices(), Lorene::Itbl::set(), Lorene::Tensor::set(), Lorene::Tensor_sym::sym_index1(), and Lorene::Tensor_sym::sym_index2().
◆ epsilon_A_minus_one()
| double Lorene::Spheroid::epsilon_A_minus_one | ( | ) | const |
Computation of the refined Penrose parameter for axisymmetric spacetimes, and its difference wrt one.
Definition at line 867 of file spheroid.C.
References angu_mom(), area(), mass(), Lorene::pow(), and Lorene::sqrt().
◆ epsilon_P_minus_one()
| double Lorene::Spheroid::epsilon_P_minus_one | ( | ) | const |
Computation of the classical Penrose parameter, and its difference wrt one.
To use in replacement of epsilon_A_minus_one when the computed spacetime is not axisymmetric.
Definition at line 879 of file spheroid.C.
References angu_mom(), area(), mass(), p_epsilon_P_minus_one, and Lorene::pow().
◆ get_ephi()
|
inline |
Returns the conformal Killing symmetry vector on the 2-surface.
Definition at line 253 of file spheroid.h.
References ephi.
◆ get_fff()
|
inline |
◆ get_ggg()
|
inline |
◆ get_hh()
|
inline |
◆ get_hsurf()
|
inline |
◆ get_issphere()
|
inline |
Returns the flag saying whether or not the horizon is geometrically round.
Definition at line 265 of file spheroid.h.
References issphere.
◆ get_jac2d()
|
inline |
returns the 2-d jacobian of coordinate transformation 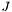
Definition at line 241 of file spheroid.h.
References jac2d.
◆ get_jj()
|
inline |
◆ get_ll()
|
inline |
◆ get_proj()
|
inline |
◆ get_qab()
|
inline |
Returns the metric 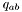 .
.
Definition at line 226 of file spheroid.h.
◆ get_qq()
|
inline |
◆ get_ricci()
|
inline |
◆ get_ss()
|
inline |
◆ get_trk()
|
inline |
◆ mass()
| double Lorene::Spheroid::mass | ( | ) | const |
Computes the mass as defined from the calculus of angular momentum, done with respect to a divergence free tangent vector field 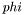 .
.
Spheroid has to be a real sphere (flag issphere true), of constant radius
![\[R_{s} \]](form_875.png)
. defined as
![\[ M = \frac{1}{2 R_{s}} \sqrt{R_{s}^{4} + 4{\cal J}^{2}} \]](form_876.png)
Definition at line 739 of file spheroid.C.
References angu_mom(), area(), p_mass, and Lorene::sqrt().
◆ multipole_angu()
| double Lorene::Spheroid::multipole_angu | ( | const int | order | ) | const |
Computes the angular multipole of a given order for the spheroid, assumed to be spherical.
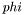 is a divergence free tangent vector field. WARNING:order has to be strictly higher than zero (no topological defects here...), and an odd number for technical reasons.
is a divergence free tangent vector field. WARNING:order has to be strictly higher than zero (no topological defects here...), and an odd number for technical reasons.
Definition at line 804 of file spheroid.C.
References area(), Lorene::contract(), Lorene::Map::get_bvect_spher(), get_ephi(), Lorene::Tensor::get_mp(), h_surf, Lorene::Map_af::integrale_surface(), jac2d, ll, p_multipole_angu, Lorene::Scalar::set_spectral_va(), Lorene::sqrt(), sqrt_q(), Lorene::Scalar::std_spectral_base(), and Lorene::Valeur::ylm().
◆ multipole_mass()
| double Lorene::Spheroid::multipole_mass | ( | const int | order | ) | const |
Computes the mass multipole of a given order for the spheroid, assumed to be spherical.
WARNING: For technical reasons, only even orders are supported by the code.
Definition at line 751 of file spheroid.C.
References area(), Lorene::Tensor::get_mp(), get_ricci(), h_surf, Lorene::Map_af::integrale_surface(), mass(), p_multipole_mass, Lorene::Scalar::set_spectral_va(), Lorene::sqrt(), sqrt_q(), Lorene::Scalar::std_spectral_base(), and Lorene::Valeur::ylm().
◆ operator=()
| void Lorene::Spheroid::operator= | ( | const Spheroid & | sph_in | ) |
◆ sauve()
|
virtual |
Save in a file.
Definition at line 1189 of file spheroid.C.
◆ set_der_0x0()
|
protected |
Sets to 0x0 all the pointers on derived quantities.
Definition at line 669 of file spheroid.C.
References p_angu_mom, p_area, p_epsilon_P_minus_one, p_mass, p_multipole_angu, p_multipole_mass, p_shear, p_sqrt_q, p_theta_minus, and p_theta_plus.
◆ set_ephi()
| void Lorene::Spheroid::set_ephi | ( | const Scalar & | ) |
Assigns the conformal Killing vector field to phi.
◆ set_fff()
|
inline |
Sets the normalization factor F.
Definition at line 298 of file spheroid.h.
References del_deriv(), and fff.
◆ set_ggg()
|
inline |
Sets the normalization factor G.
Definition at line 301 of file spheroid.h.
References del_deriv(), and ggg.
◆ set_hh()
|
inline |
Sets the symmetric tensor 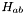 .
.
Definition at line 283 of file spheroid.h.
References del_deriv(), and hh.
◆ set_hsurf()
|
inline |
Sets the field h_surf.
Definition at line 268 of file spheroid.h.
References del_deriv(), and h_surf.
◆ set_issphere()
|
inline |
Sets the boolean linked to geometrical shape of the horizon.
Definition at line 304 of file spheroid.h.
References del_deriv(), and issphere.
◆ set_jj()
|
inline |
Sets the symmetric tensor 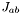 .
.
Definition at line 295 of file spheroid.h.
References del_deriv(), and jj.
◆ set_ll()
|
inline |
◆ set_proj()
|
inline |
◆ set_qab()
|
inline |
Sets the modified metric (non degenerated) 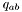 .
.
Definition at line 271 of file spheroid.h.
References del_deriv().
◆ set_qq()
|
inline |
Sets the degenerated metric 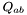 .
.
Definition at line 277 of file spheroid.h.
References del_deriv(), and qq.
◆ set_ricci()
|
inline |
Sets the 2-Ricci scalar 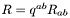 .
.
Definition at line 274 of file spheroid.h.
References del_deriv(), and ricci.
◆ set_ss()
|
inline |
◆ set_trk()
|
inline |
Sets the trace K on the 2-surface.
Definition at line 286 of file spheroid.h.
References del_deriv(), and trk.
◆ shear()
| const Sym_tensor & Lorene::Spheroid::shear | ( | ) | const |
Computes the shear of the 2-surface 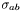 .
.
Definition at line 928 of file spheroid.C.
References Lorene::Metric::cov(), fff, hh, jj, p_shear, Lorene::Tensor::std_spectral_base(), and Lorene::Tensor::trace().
◆ sqrt_q()
| const Scalar & Lorene::Spheroid::sqrt_q | ( | ) | const |
Computes the normal vector field to the 2-surface.
Computes the square root of the determinant of 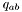 .
.
Definition at line 696 of file spheroid.C.
References get_qq(), p_sqrt_q, Lorene::sqrt(), and Lorene::Scalar::std_spectral_base().
◆ theta_minus()
| const Scalar & Lorene::Spheroid::theta_minus | ( | ) | const |
Computes the ingoing null expansion 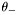 .
.
Definition at line 912 of file spheroid.C.
References ggg, hh, jj, p_theta_minus, Lorene::Scalar::std_spectral_base(), and Lorene::Tensor::trace().
◆ theta_plus()
| const Scalar & Lorene::Spheroid::theta_plus | ( | ) | const |
Computes the outgoing null expansion 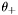 .
.
Definition at line 892 of file spheroid.C.
References fff, hh, jj, p_theta_plus, Lorene::Scalar::set_spectral_va(), Lorene::Scalar::std_spectral_base(), Lorene::Tensor::trace(), and Lorene::Valeur::ylm().
◆ update_from_tslice()
| void Lorene::Spheroid::update_from_tslice | ( | const Metric & | gamij, |
| const Sym_tensor & | Kij | ||
| ) |
Updates from the 3-slice data.
Friends And Related Function Documentation
◆ operator<<
|
friend |
Display.
Member Data Documentation
◆ ephi
|
protected |
The conformal Killing vector field on the 2-surface (set to by default to the axial vector associated with coordinate 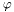 )
)
Definition at line 113 of file spheroid.h.
◆ fff
|
protected |
Normalization function for the outgoing null vector l.
Definition at line 138 of file spheroid.h.
◆ ggg
|
protected |
Normalization function for the ingoing null vector k.
Definition at line 143 of file spheroid.h.
◆ h_surf
|
protected |
The location of the 2-surface as r = h_surf 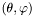 .
.
Definition at line 91 of file spheroid.h.
◆ hh
|
protected |
The ricci scalar on the 2-surface.
Extrinsic curvature of the 2-surface in the 3-slice. 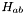 (covariant representation)
(covariant representation)
Definition at line 122 of file spheroid.h.
◆ issphere
|
protected |
Flag to know whether the horizon is geometrically round or distorted.
Definition at line 151 of file spheroid.h.
◆ jac2d
|
protected |
The jacobian of the adaptation of coordinates (contravariant/covariant representation)
Definition at line 96 of file spheroid.h.
◆ jj
|
protected |
Tangent components of the extrinsic curvature of the 3-slice.
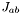 (covariant representation)
(covariant representation)
Definition at line 134 of file spheroid.h.
◆ ll
|
protected |
Normal-tangent component of the extrinsic curvature of the 3-slice.
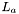 (covariant representation)
(covariant representation)
Definition at line 129 of file spheroid.h.
◆ p_angu_mom
|
mutableprotected |
The angular momentum.
Definition at line 159 of file spheroid.h.
◆ p_area
|
mutableprotected |
The area of the 2-surface.
Definition at line 158 of file spheroid.h.
◆ p_epsilon_P_minus_one
|
mutableprotected |
Refined Penrose parameter, difference wrt one.
Definition at line 164 of file spheroid.h.
◆ p_mass
|
mutableprotected |
Mass defined from angular momentum.
Definition at line 160 of file spheroid.h.
◆ p_multipole_angu
|
mutableprotected |
Angular momentum multipole for the spheroid.
Definition at line 162 of file spheroid.h.
◆ p_multipole_mass
|
mutableprotected |
Mass multipole for the spheroid.
Definition at line 161 of file spheroid.h.
◆ p_shear
|
mutableprotected |
The shear tensor.
Definition at line 167 of file spheroid.h.
◆ p_sqrt_q
|
mutableprotected |
Surface element 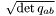 .
.
Definition at line 157 of file spheroid.h.
◆ p_theta_minus
|
mutableprotected |
Null ingoing expansion.
Definition at line 166 of file spheroid.h.
◆ p_theta_plus
|
mutableprotected |
Classical Penrose parameter, difference wrt one.
Null outgoing expansion
Definition at line 165 of file spheroid.h.
◆ proj
|
protected |
The 3-d projector on the 2-surface (contravariant-covariant form).
Definition at line 100 of file spheroid.h.
|
protected |
The 3-d covariant degenerated 2-metric on the surface.
Definition at line 104 of file spheroid.h.
◆ ricci
|
protected |
Induced metric on the 2-surface 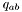 .
.
Definition at line 117 of file spheroid.h.
◆ ss
|
protected |
The adapted normal vector field to spheroid in the 3-slice.
Definition at line 108 of file spheroid.h.
◆ trk
|
protected |
Trace K of the extrinsic curvature of the 3-slice.
Definition at line 124 of file spheroid.h.
The documentation for this class was generated from the following files:
