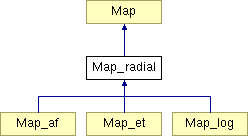
Map_radial Class Reference
[Mapping grid -> physical space (spherical coordinates)]
Base class for pure radial mappings. More...
#include <map.h>
Public Member Functions | |
| virtual | ~Map_radial () |
| Destructor. | |
| virtual void | operator= (const Map_af &)=0 |
| Assignment to an affine mapping. | |
| virtual void | sauve (FILE *) const |
| Save in a file. | |
| virtual double | val_r_jk (int l, double xi, int j, int k) const =0 |
Returns the value of the radial coordinate r for a given  and a given collocation point in and a given collocation point in 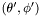 in a given domain. in a given domain. | |
| virtual void | val_lx_jk (double rr, int j, int k, const Param &par, int &l, double &xi) const =0 |
Computes the domain index l and the value of  corresponding to a point of arbitrary r but collocation values of corresponding to a point of arbitrary r but collocation values of 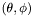 . . | |
| virtual bool | operator== (const Map &) const =0 |
| Comparison operator (egality). | |
| virtual void | reevaluate (const Map *mp_prev, int nzet, Cmp &uu) const |
Recomputes the values of a Cmp at the collocation points after a change in the mapping. | |
| virtual void | reevaluate_symy (const Map *mp_prev, int nzet, Cmp &uu) const |
Recomputes the values of a Cmp at the collocation points after a change in the mapping. | |
| virtual void | reevaluate (const Map *mp_prev, int nzet, Scalar &uu) const |
Recomputes the values of a Scalar at the collocation points after a change in the mapping. | |
| virtual void | reevaluate_symy (const Map *mp_prev, int nzet, Scalar &uu) const |
Recomputes the values of a Scalar at the collocation points after a change in the mapping. | |
| virtual void | mult_r (Scalar &uu) const |
Multiplication by r of a Scalar, the dzpuis of uu is not changed. | |
| virtual void | mult_r (Cmp &ci) const |
Multiplication by r of a Cmp. | |
| virtual void | mult_r_zec (Scalar &) const |
Multiplication by r (in the compactified external domain only) of a Scalar. | |
| virtual void | mult_rsint (Scalar &) const |
Multiplication by 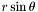 of a of a Scalar. | |
| virtual void | div_rsint (Scalar &) const |
Division by 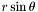 of a of a Scalar. | |
| virtual void | div_r (Scalar &) const |
Division by r of a Scalar. | |
| virtual void | div_r_zec (Scalar &) const |
Division by r (in the compactified external domain only) of a Scalar. | |
| virtual void | mult_cost (Scalar &) const |
Multiplication by 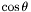 of a of a Scalar. | |
| virtual void | div_cost (Scalar &) const |
Division by 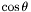 of a of a Scalar. | |
| virtual void | mult_sint (Scalar &) const |
Multiplication by 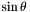 of a of a Scalar. | |
| virtual void | div_sint (Scalar &) const |
Division by 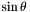 of a of a Scalar. | |
| virtual void | div_tant (Scalar &) const |
Division by 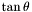 of a of a Scalar. | |
| virtual void | comp_x_from_spherical (const Scalar &v_r, const Scalar &v_theta, const Scalar &v_phi, Scalar &v_x) const |
Computes the Cartesian x component (with respect to bvect_cart) of a vector given by its spherical components with respect to bvect_spher. | |
| virtual void | comp_x_from_spherical (const Cmp &v_r, const Cmp &v_theta, const Cmp &v_phi, Cmp &v_x) const |
Cmp version | |
| virtual void | comp_y_from_spherical (const Scalar &v_r, const Scalar &v_theta, const Scalar &v_phi, Scalar &v_y) const |
Computes the Cartesian y component (with respect to bvect_cart ) of a vector given by its spherical components with respect to bvect_spher . | |
| virtual void | comp_y_from_spherical (const Cmp &v_r, const Cmp &v_theta, const Cmp &v_phi, Cmp &v_y) const |
Cmp version | |
| virtual void | comp_z_from_spherical (const Scalar &v_r, const Scalar &v_theta, Scalar &v_z) const |
Computes the Cartesian z component (with respect to bvect_cart ) of a vector given by its spherical components with respect to bvect_spher . | |
| virtual void | comp_z_from_spherical (const Cmp &v_r, const Cmp &v_theta, Cmp &v_z) const |
Cmp version | |
| virtual void | comp_r_from_cartesian (const Scalar &v_x, const Scalar &v_y, const Scalar &v_z, Scalar &v_r) const |
Computes the Spherical r component (with respect to bvect_spher ) of a vector given by its cartesian components with respect to bvect_cart . | |
| virtual void | comp_r_from_cartesian (const Cmp &v_x, const Cmp &v_y, const Cmp &v_z, Cmp &v_r) const |
Cmp version | |
| virtual void | comp_t_from_cartesian (const Scalar &v_x, const Scalar &v_y, const Scalar &v_z, Scalar &v_t) const |
Computes the Spherical  component (with respect to component (with respect to bvect_spher ) of a vector given by its cartesian components with respect to bvect_cart . | |
| virtual void | comp_t_from_cartesian (const Cmp &v_x, const Cmp &v_y, const Cmp &v_z, Cmp &v_t) const |
Cmp version | |
| virtual void | comp_p_from_cartesian (const Scalar &v_x, const Scalar &v_y, Scalar &v_p) const |
Computes the Spherical  component (with respect to component (with respect to bvect_spher ) of a vector given by its cartesian components with respect to bvect_cart . | |
| virtual void | comp_p_from_cartesian (const Cmp &v_x, const Cmp &v_y, Cmp &v_p) const |
Cmp version | |
| virtual void | dec_dzpuis (Scalar &) const |
Decreases by 1 the value of dzpuis of a Scalar and changes accordingly its values in the compactified external domain (CED). | |
| virtual void | dec2_dzpuis (Scalar &) const |
Decreases by 2 the value of dzpuis of a Scalar and changes accordingly its values in the compactified external domain (CED). | |
| virtual void | inc_dzpuis (Scalar &) const |
Increases by 1 the value of dzpuis of a Scalar and changes accordingly its values in the compactified external domain (CED). | |
| virtual void | inc2_dzpuis (Scalar &) const |
Increases by 2 the value of dzpuis of a Scalar and changes accordingly its values in the compactified external domain (CED). | |
| virtual void | poisson_compact (const Cmp &source, const Cmp &aa, const Tenseur &bb, const Param &par, Cmp &psi) const |
Resolution of the elliptic equation 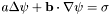 in the case where the stellar interior is covered by a single domain. in the case where the stellar interior is covered by a single domain. | |
| virtual void | poisson_compact (int nzet, const Cmp &source, const Cmp &aa, const Tenseur &bb, const Param &par, Cmp &psi) const |
Resolution of the elliptic equation 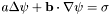 in the case of a multidomain stellar interior. in the case of a multidomain stellar interior. | |
| const Mg3d * | get_mg () const |
Gives the Mg3d on which the mapping is defined. | |
| double | get_ori_x () const |
| Returns the x coordinate of the origin. | |
| double | get_ori_y () const |
| Returns the y coordinate of the origin. | |
| double | get_ori_z () const |
| Returns the z coordinate of the origin. | |
| double | get_rot_phi () const |
| Returns the angle between the x --axis and X --axis. | |
| const Base_vect_spher & | get_bvect_spher () const |
Returns the orthonormal vectorial basis 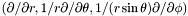 associated with the coordinates associated with the coordinates 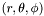 of the mapping. of the mapping. | |
| const Base_vect_cart & | get_bvect_cart () const |
Returns the Cartesian basis 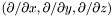 associated with the coordinates (x,y,z) of the mapping, i.e. associated with the coordinates (x,y,z) of the mapping, i.e. | |
| const Metric_flat & | flat_met_spher () const |
Returns the flat metric associated with the spherical coordinates and with components expressed in the triad bvect_spher. | |
| const Metric_flat & | flat_met_cart () const |
Returns the flat metric associated with the Cartesian coordinates and with components expressed in the triad bvect_cart. | |
| const Cmp & | cmp_zero () const |
Returns the null Cmp defined on *this. | |
| virtual const Map_af & | mp_angu (int) const =0 |
Returns the "angular" mapping for the outside of domain l_zone. | |
| void | convert_absolute (double xx, double yy, double zz, double &rr, double &theta, double &pphi) const |
Determines the coordinates 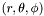 corresponding to given absolute Cartesian coordinates (X,Y,Z). corresponding to given absolute Cartesian coordinates (X,Y,Z). | |
| virtual double | val_r (int l, double xi, double theta, double pphi) const =0 |
Returns the value of the radial coordinate r for a given 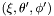 in a given domain. in a given domain. | |
| virtual void | val_lx (double rr, double theta, double pphi, int &l, double &xi) const =0 |
Computes the domain index l and the value of  corresponding to a point given by its physical coordinates corresponding to a point given by its physical coordinates 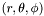 . . | |
| virtual void | val_lx (double rr, double theta, double pphi, const Param &par, int &l, double &xi) const =0 |
Computes the domain index l and the value of  corresponding to a point given by its physical coordinates corresponding to a point given by its physical coordinates 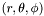 . . | |
| virtual bool | operator== (const Map &) const =0 |
| Comparison operator (egality). | |
| void | set_ori (double xa0, double ya0, double za0) |
| Sets a new origin. | |
| void | set_rot_phi (double phi0) |
| Sets a new rotation angle. | |
| virtual void | homothetie (double lambda)=0 |
| Sets a new radial scale. | |
| virtual void | resize (int l, double lambda)=0 |
| Rescales the outer boundary of one domain. | |
| virtual void | adapt (const Cmp &ent, const Param &par, int nbr=0)=0 |
| Adaptation of the mapping to a given scalar field. | |
| virtual void | reevaluate (const Map *mp_prev, int nzet, Cmp &uu) const =0 |
Recomputes the values of a Cmp at the collocation points after a change in the mapping. | |
| virtual void | reevaluate (const Map *mp_prev, int nzet, Scalar &uu) const =0 |
Recomputes the values of a Scalar at the collocation points after a change in the mapping. | |
| virtual void | reevaluate_symy (const Map *mp_prev, int nzet, Cmp &uu) const =0 |
Recomputes the values of a Cmp at the collocation points after a change in the mapping. | |
| virtual void | reevaluate_symy (const Map *mp_prev, int nzet, Scalar &uu) const =0 |
Recomputes the values of a Scalar at the collocation points after a change in the mapping. | |
| virtual void | dsdxi (const Cmp &ci, Cmp &resu) const =0 |
Computes 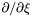 of a of a Cmp . | |
| virtual void | dsdxi (const Scalar &uu, Scalar &resu) const =0 |
Computes 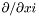 of a of a Scalar . | |
| virtual void | dsdr (const Cmp &ci, Cmp &resu) const =0 |
Computes 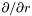 of a of a Cmp . | |
| virtual void | dsdr (const Scalar &uu, Scalar &resu) const =0 |
Computes 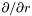 of a of a Scalar . | |
| virtual void | srdsdt (const Cmp &ci, Cmp &resu) const =0 |
Computes 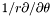 of a of a Cmp . | |
| virtual void | srdsdt (const Scalar &uu, Scalar &resu) const =0 |
Computes 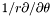 of a of a Scalar . | |
| virtual void | srstdsdp (const Cmp &ci, Cmp &resu) const =0 |
Computes 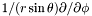 of a of a Cmp . | |
| virtual void | srstdsdp (const Scalar &uu, Scalar &resu) const =0 |
Computes 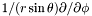 of a of a Scalar . | |
| virtual void | dsdradial (const Scalar &uu, Scalar &resu) const =0 |
Computes 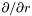 of a of a Scalar if the description is affine and 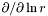 if it is logarithmic. if it is logarithmic. | |
| virtual void | dsdt (const Scalar &uu, Scalar &resu) const =0 |
Computes 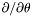 of a of a Scalar . | |
| virtual void | stdsdp (const Scalar &uu, Scalar &resu) const =0 |
Computes 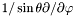 of a of a Scalar . | |
| virtual void | laplacien (const Scalar &uu, int zec_mult_r, Scalar &lap) const =0 |
| Computes the Laplacian of a scalar field. | |
| virtual void | laplacien (const Cmp &uu, int zec_mult_r, Cmp &lap) const =0 |
Computes the Laplacian of a scalar field (Cmp version). | |
| virtual void | lapang (const Scalar &uu, Scalar &lap) const =0 |
| Computes the angular Laplacian of a scalar field. | |
| virtual void | primr (const Scalar &uu, Scalar &resu, bool null_infty) const =0 |
Computes the radial primitive which vanishes for 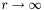 . . | |
| virtual Tbl * | integrale (const Cmp &) const =0 |
Computes the integral over all space of a Cmp . | |
| virtual void | poisson (const Cmp &source, Param &par, Cmp &uu) const =0 |
| Computes the solution of a scalar Poisson equation. | |
| virtual void | poisson_tau (const Cmp &source, Param &par, Cmp &uu) const =0 |
| Computes the solution of a scalar Poisson equationwith a Tau method. | |
| virtual void | poisson_falloff (const Cmp &source, Param &par, Cmp &uu, int k_falloff) const =0 |
| virtual void | poisson_ylm (const Cmp &source, Param &par, Cmp &pot, int nylm, double *intvec) const =0 |
| virtual void | poisson_regular (const Cmp &source, int k_div, int nzet, double unsgam1, Param &par, Cmp &uu, Cmp &uu_regu, Cmp &uu_div, Tenseur &duu_div, Cmp &source_regu, Cmp &source_div) const =0 |
| Computes the solution of a scalar Poisson equation. | |
| virtual void | poisson_angu (const Scalar &source, Param &par, Scalar &uu, double lambda=0) const =0 |
| Computes the solution of the generalized angular Poisson equation. | |
| virtual Param * | donne_para_poisson_vect (Param ¶, int i) const =0 |
Function intended to be used by Map::poisson_vect and Map::poisson_vect_oohara . | |
| virtual void | poisson_frontiere (const Cmp &source, const Valeur &limite, int raccord, int num_front, Cmp &pot, double=0., double=0.) const =0 |
Computes the solution of a Poisson equation from the domain num_front+1 . | |
| virtual void | poisson_frontiere_double (const Cmp &source, const Valeur &lim_func, const Valeur &lim_der, int num_zone, Cmp &pot) const =0 |
| virtual void | poisson_interne (const Cmp &source, const Valeur &limite, Param &par, Cmp &pot) const =0 |
| Computes the solution of a Poisson equation in the shell, imposing a boundary condition at the surface of the star. | |
| virtual void | poisson2d (const Cmp &source_mat, const Cmp &source_quad, Param &par, Cmp &uu) const =0 |
| Computes the solution of a 2-D Poisson equation. | |
| virtual void | dalembert (Param &par, Scalar &fJp1, const Scalar &fJ, const Scalar &fJm1, const Scalar &source) const =0 |
| Performs one time-step integration of the d'Alembert scalar equation. | |
Public Attributes | |
| Coord | xsr |
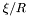 in the nucleus; \ 1/R in the non-compactified shells; \ in the nucleus; \ 1/R in the non-compactified shells; \ 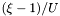 in the compactified outer domain. in the compactified outer domain. | |
| Coord | dxdr |
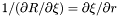 in the nucleus and in the non-compactified shells; \ in the nucleus and in the non-compactified shells; \ 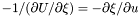 in the compactified outer domain. in the compactified outer domain. | |
| Coord | drdt |
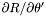 in the nucleus and in the non-compactified shells; \ in the nucleus and in the non-compactified shells; \ 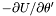 in the compactified external domain (CED). in the compactified external domain (CED). | |
| Coord | stdrdp |
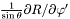 in the nucleus and in the non-compactified shells; \ in the nucleus and in the non-compactified shells; \ 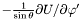 in the compactified external domain (CED). in the compactified external domain (CED). | |
| Coord | srdrdt |
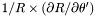 in the nucleus and in the non-compactified shells; \ in the nucleus and in the non-compactified shells; \ 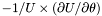 in the compactified outer domain. in the compactified outer domain. | |
| Coord | srstdrdp |
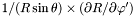 in the nucleus and in the non-compactified shells; \ in the nucleus and in the non-compactified shells; \ 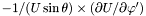 in the compactified outer domain. in the compactified outer domain. | |
| Coord | sr2drdt |
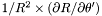 in the nucleus and in the non-compactified shells; \ in the nucleus and in the non-compactified shells; \ 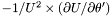 in the compactified outer domain. in the compactified outer domain. | |
| Coord | sr2stdrdp |
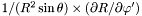 in the nucleus and in the non-compactified shells; \ in the nucleus and in the non-compactified shells; \ 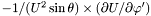 in the compactified outer domain. in the compactified outer domain. | |
| Coord | d2rdx2 |
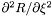 in the nucleus and in the non-compactified shells; \ in the nucleus and in the non-compactified shells; \ 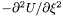 in the compactified outer domain. in the compactified outer domain. | |
| Coord | lapr_tp |
![$1/R^2 \times [ 1/\sin(\theta)\times \partial /\partial\theta' (\sin\theta \partial R /\partial\theta') + 1/\sin^2\theta \partial^2 R /\partial{\varphi'}^2] $](form_535.png) in the nucleus and in the non-compactified shells; \ in the nucleus and in the non-compactified shells; \ ![$- 1/U^2 \times [ 1/\sin(\theta)\times \partial /\partial\theta' (\sin\theta \partial U /\partial\theta') + 1/\sin^2\theta \partial^2 U /\partial{\varphi'}^2] $](form_536.png) in the compactified outer domain. in the compactified outer domain. | |
| Coord | d2rdtdx |
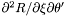 in the nucleus and in the non-compactified shells; \ in the nucleus and in the non-compactified shells; \ 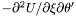 in the compactified outer domain. in the compactified outer domain. | |
| Coord | sstd2rdpdx |
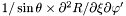 in the nucleus and in the non-compactified shells; \ in the nucleus and in the non-compactified shells; \ 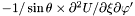 in the compactified outer domain. in the compactified outer domain. | |
| Coord | sr2d2rdt2 |
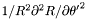 in the nucleus and in the non-compactified shells; \ in the nucleus and in the non-compactified shells; \ 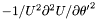 in the compactified outer domain. in the compactified outer domain. | |
| Coord | r |
| r coordinate centered on the grid | |
| Coord | tet |
 coordinate centered on the grid coordinate centered on the grid | |
| Coord | phi |
 coordinate centered on the grid coordinate centered on the grid | |
| Coord | sint |
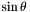 | |
| Coord | cost |
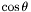 | |
| Coord | sinp |
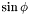 | |
| Coord | cosp |
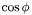 | |
| Coord | x |
| x coordinate centered on the grid | |
| Coord | y |
| y coordinate centered on the grid | |
| Coord | z |
| z coordinate centered on the grid | |
| Coord | xa |
| Absolute x coordinate. | |
| Coord | ya |
| Absolute y coordinate. | |
| Coord | za |
| Absolute z coordinate. | |
Protected Member Functions | |
| Map_radial (const Mg3d &mgrid) | |
Constructor from a grid (protected to make Map_radial an abstract class). | |
| Map_radial (const Map_radial &mp) | |
| Copy constructor. | |
| Map_radial (const Mg3d &, FILE *) | |
Constructor from a file (see sauve(FILE* ) ). | |
| virtual void | reset_coord () |
Resets all the member Coords. | |
Protected Attributes | |
| const Mg3d * | mg |
Pointer on the multi-grid Mgd3 on which this is defined. | |
| double | ori_x |
| Absolute coordinate x of the origin. | |
| double | ori_y |
| Absolute coordinate y of the origin. | |
| double | ori_z |
| Absolute coordinate z of the origin. | |
| double | rot_phi |
| Angle between the x --axis and X --axis. | |
| Base_vect_spher | bvect_spher |
Orthonormal vectorial basis 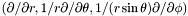 associated with the coordinates associated with the coordinates 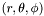 of the mapping. of the mapping. | |
| Base_vect_cart | bvect_cart |
Cartesian basis 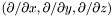 associated with the coordinates (x,y,z) of the mapping, i.e. associated with the coordinates (x,y,z) of the mapping, i.e. | |
| Metric_flat * | p_flat_met_spher |
Pointer onto the flat metric associated with the spherical coordinates and with components expressed in the triad bvect_spher. | |
| Metric_flat * | p_flat_met_cart |
Pointer onto the flat metric associated with the Cartesian coordinates and with components expressed in the triad bvect_cart. | |
| Cmp * | p_cmp_zero |
| The null Cmp. | |
| Map_af * | p_mp_angu |
| Pointer on the "angular" mapping. | |
Friends | |
| ostream & | operator<< (ostream &, const Map &) |
| Operator <<. | |
Detailed Description
Base class for pure radial mappings.
()
A pure radial mapping is a mapping of the type  ,
, 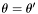 ,
, 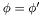 . The class
. The class Map_radial is an abstract class. Effective implementations of radial mapping are performed by the derived class Map_af and Map_et .
Definition at line 1532 of file map.h.
Constructor & Destructor Documentation
| Map_radial::Map_radial | ( | const Mg3d & | mgrid | ) | [protected] |
Constructor from a grid (protected to make Map_radial an abstract class).
Definition at line 85 of file map_radial.C.
| Map_radial::Map_radial | ( | const Map_radial & | mp | ) | [protected] |
Copy constructor.
Definition at line 92 of file map_radial.C.
| Map_radial::Map_radial | ( | const Mg3d & | mgi, | |
| FILE * | fd | |||
| ) | [protected] |
Constructor from a file (see sauve(FILE* ) ).
Definition at line 99 of file map_radial.C.
| Map_radial::~Map_radial | ( | ) | [virtual] |
Destructor.
Definition at line 106 of file map_radial.C.
Member Function Documentation
| const Cmp& Map::cmp_zero | ( | ) | const [inline, inherited] |
| void Map_radial::comp_p_from_cartesian | ( | const Cmp & | v_x, | |
| const Cmp & | v_y, | |||
| Cmp & | v_p | |||
| ) | const [virtual] |
Cmp version
Implements Map.
Definition at line 172 of file map_radial_comp_rtp.C.
References comp_p_from_cartesian().
| void Map_radial::comp_p_from_cartesian | ( | const Scalar & | v_x, | |
| const Scalar & | v_y, | |||
| Scalar & | v_p | |||
| ) | const [virtual] |
Computes the Spherical  component (with respect to
component (with respect to bvect_spher ) of a vector given by its cartesian components with respect to bvect_cart .
- Parameters:
-
v_x [input] x-component of the vector v_y [input] y-component of the vector v_p [output]  -component of the vector
-component of the vector
Implements Map.
Definition at line 179 of file map_radial_comp_rtp.C.
References Scalar::check_dzpuis(), Scalar::dz_nonzero(), Scalar::get_dzpuis(), Scalar::get_etat(), Tensor::get_mp(), Scalar::get_spectral_va(), Valeur::mult_cp(), and Scalar::set_dzpuis().
| void Map_radial::comp_r_from_cartesian | ( | const Cmp & | v_x, | |
| const Cmp & | v_y, | |||
| const Cmp & | v_z, | |||
| Cmp & | v_r | |||
| ) | const [virtual] |
Cmp version
Implements Map.
Definition at line 61 of file map_radial_comp_rtp.C.
References comp_r_from_cartesian().
| void Map_radial::comp_r_from_cartesian | ( | const Scalar & | v_x, | |
| const Scalar & | v_y, | |||
| const Scalar & | v_z, | |||
| Scalar & | v_r | |||
| ) | const [virtual] |
Computes the Spherical r component (with respect to bvect_spher ) of a vector given by its cartesian components with respect to bvect_cart .
- Parameters:
-
v_x [input] x-component of the vector v_y [input] y-component of the vector v_z [input] z-component of the vector v_r [output] r -component of the vector
Implements Map.
Definition at line 68 of file map_radial_comp_rtp.C.
References Scalar::check_dzpuis(), Scalar::dz_nonzero(), Scalar::get_dzpuis(), Scalar::get_etat(), Tensor::get_mp(), Scalar::get_spectral_va(), Valeur::mult_cp(), Valeur::mult_ct(), Valeur::mult_sp(), Valeur::mult_st(), and Scalar::set_dzpuis().
| void Map_radial::comp_t_from_cartesian | ( | const Cmp & | v_x, | |
| const Cmp & | v_y, | |||
| const Cmp & | v_z, | |||
| Cmp & | v_t | |||
| ) | const [virtual] |
Cmp version
Implements Map.
Definition at line 117 of file map_radial_comp_rtp.C.
References comp_t_from_cartesian().
| void Map_radial::comp_t_from_cartesian | ( | const Scalar & | v_x, | |
| const Scalar & | v_y, | |||
| const Scalar & | v_z, | |||
| Scalar & | v_t | |||
| ) | const [virtual] |
Computes the Spherical  component (with respect to
component (with respect to bvect_spher ) of a vector given by its cartesian components with respect to bvect_cart .
- Parameters:
-
v_x [input] x-component of the vector v_y [input] y-component of the vector v_z [input] z-component of the vector v_t [output]  -component of the vector
-component of the vector
Implements Map.
Definition at line 124 of file map_radial_comp_rtp.C.
References Scalar::check_dzpuis(), Scalar::dz_nonzero(), Scalar::get_dzpuis(), Scalar::get_etat(), Tensor::get_mp(), Scalar::get_spectral_va(), Valeur::mult_cp(), Valeur::mult_ct(), Valeur::mult_sp(), Valeur::mult_st(), and Scalar::set_dzpuis().
| void Map_radial::comp_x_from_spherical | ( | const Cmp & | v_r, | |
| const Cmp & | v_theta, | |||
| const Cmp & | v_phi, | |||
| Cmp & | v_x | |||
| ) | const [virtual] |
Cmp version
Implements Map.
Definition at line 64 of file map_radial_comp_xyz.C.
References comp_x_from_spherical().
| void Map_radial::comp_x_from_spherical | ( | const Scalar & | v_r, | |
| const Scalar & | v_theta, | |||
| const Scalar & | v_phi, | |||
| Scalar & | v_x | |||
| ) | const [virtual] |
Computes the Cartesian x component (with respect to bvect_cart) of a vector given by its spherical components with respect to bvect_spher.
- Parameters:
-
v_r [input] r -component of the vector v_theta [input]  -component of the vector
-component of the vector v_phi [input]  -component of the vector
-component of the vector v_x [output] x-component of the vector
Implements Map.
Definition at line 72 of file map_radial_comp_xyz.C.
References Scalar::check_dzpuis(), Scalar::dz_nonzero(), Scalar::get_dzpuis(), Scalar::get_etat(), Tensor::get_mp(), Scalar::get_spectral_va(), Valeur::mult_cp(), Valeur::mult_ct(), Valeur::mult_sp(), Valeur::mult_st(), and Scalar::set_dzpuis().
| void Map_radial::comp_y_from_spherical | ( | const Cmp & | v_r, | |
| const Cmp & | v_theta, | |||
| const Cmp & | v_phi, | |||
| Cmp & | v_y | |||
| ) | const [virtual] |
Cmp version
Implements Map.
Definition at line 122 of file map_radial_comp_xyz.C.
References comp_y_from_spherical().
| void Map_radial::comp_y_from_spherical | ( | const Scalar & | v_r, | |
| const Scalar & | v_theta, | |||
| const Scalar & | v_phi, | |||
| Scalar & | v_y | |||
| ) | const [virtual] |
Computes the Cartesian y component (with respect to bvect_cart ) of a vector given by its spherical components with respect to bvect_spher .
- Parameters:
-
v_r [input] r -component of the vector v_theta [input]  -component of the vector
-component of the vector v_phi [input]  -component of the vector
-component of the vector v_y [output] y-component of the vector
Implements Map.
Definition at line 131 of file map_radial_comp_xyz.C.
References Scalar::check_dzpuis(), Scalar::dz_nonzero(), Scalar::get_dzpuis(), Scalar::get_etat(), Tensor::get_mp(), Scalar::get_spectral_va(), Valeur::mult_cp(), Valeur::mult_ct(), Valeur::mult_sp(), Valeur::mult_st(), and Scalar::set_dzpuis().
| void Map_radial::comp_z_from_spherical | ( | const Cmp & | v_r, | |
| const Cmp & | v_theta, | |||
| Cmp & | v_z | |||
| ) | const [virtual] |
Cmp version
Implements Map.
Definition at line 180 of file map_radial_comp_xyz.C.
References comp_z_from_spherical().
| void Map_radial::comp_z_from_spherical | ( | const Scalar & | v_r, | |
| const Scalar & | v_theta, | |||
| Scalar & | v_z | |||
| ) | const [virtual] |
Computes the Cartesian z component (with respect to bvect_cart ) of a vector given by its spherical components with respect to bvect_spher .
- Parameters:
-
v_r [input] r -component of the vector v_theta [input]  -component of the vector
-component of the vector v_z [output] z-component of the vector
Implements Map.
Definition at line 188 of file map_radial_comp_xyz.C.
References Scalar::check_dzpuis(), Scalar::dz_nonzero(), Scalar::get_dzpuis(), Scalar::get_etat(), Tensor::get_mp(), Scalar::get_spectral_va(), Valeur::mult_st(), and Scalar::set_dzpuis().
| void Map::convert_absolute | ( | double | xx, | |
| double | yy, | |||
| double | zz, | |||
| double & | rr, | |||
| double & | theta, | |||
| double & | pphi | |||
| ) | const [inherited] |
Determines the coordinates 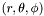 corresponding to given absolute Cartesian coordinates (X,Y,Z).
corresponding to given absolute Cartesian coordinates (X,Y,Z).
- Parameters:
-
xx [input] value of the coordinate x (absolute frame) yy [input] value of the coordinate y (absolute frame) zz [input] value of the coordinate z (absolute frame) rr [output] value of r theta [output] value of 
pphi [output] value of 
Definition at line 298 of file map.C.
References Map::ori_x, Map::ori_y, Map::ori_z, Map::rot_phi, and sqrt().
| virtual void Map::dalembert | ( | Param & | par, | |
| Scalar & | fJp1, | |||
| const Scalar & | fJ, | |||
| const Scalar & | fJm1, | |||
| const Scalar & | source | |||
| ) | const [pure virtual, inherited] |
Performs one time-step integration of the d'Alembert scalar equation.
- Parameters:
-
par [input/output] possible parameters to control the resolution of the wave equation. See the actual implementation in the derived class of Mapfor documentation. Note that, at least, param must contain the time step as firstdoubleparameter.fJp1 [output] solution 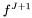 at time J+1 with boundary conditions of outgoing radiation (not exact!)
at time J+1 with boundary conditions of outgoing radiation (not exact!) fJ [input] solution 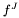 at time J
at time J fJm1 [input] solution 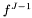 at time J-1
at time J-1 source [input] source  of the d'Alembert equation
of the d'Alembert equation 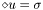 .
.
| void Map_radial::dec2_dzpuis | ( | Scalar & | ci | ) | const [virtual] |
Decreases by 2 the value of dzpuis of a Scalar and changes accordingly its values in the compactified external domain (CED).
Implements Map.
Definition at line 744 of file map_radial_r_manip.C.
References Valeur::annule(), Scalar::get_dzpuis(), Scalar::get_etat(), Valeur::get_mg(), Mg3d::get_nzone(), Mg3d::get_type_r(), Map::mg, Scalar::set_dzpuis(), Scalar::set_etat_qcq(), Scalar::set_spectral_va(), and xsr.
| void Map_radial::dec_dzpuis | ( | Scalar & | ci | ) | const [virtual] |
Decreases by 1 the value of dzpuis of a Scalar and changes accordingly its values in the compactified external domain (CED).
Implements Map.
Definition at line 639 of file map_radial_r_manip.C.
References Valeur::annule(), Scalar::get_dzpuis(), Scalar::get_etat(), Valeur::get_mg(), Mg3d::get_nzone(), Mg3d::get_type_r(), Map::mg, Scalar::set_dzpuis(), Scalar::set_etat_qcq(), Scalar::set_spectral_va(), and xsr.
| void Map_radial::div_cost | ( | Scalar & | ci | ) | const [virtual] |
Division by 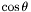 of a
of a Scalar.
Implements Map.
Definition at line 81 of file map_radial_th_manip.C.
References Scalar::get_etat(), Valeur::get_mg(), Map::mg, Valeur::scost(), Scalar::set_etat_qcq(), and Scalar::set_spectral_va().
| void Map_radial::div_r | ( | Scalar & | ci | ) | const [virtual] |
Division by r of a Scalar.
Implements Map.
Definition at line 510 of file map_radial_r_manip.C.
References Scalar::annule(), Tensor::annule_domain(), Valeur::base, Scalar::get_etat(), Valeur::get_mg(), Mg3d::get_nzone(), Mg3d::get_type_r(), Map::mg, Valeur::mult_x(), Scalar::set_etat_qcq(), Scalar::set_spectral_va(), Valeur::sx(), and xsr.
| void Map_radial::div_r_zec | ( | Scalar & | uu | ) | const [virtual] |
Division by r (in the compactified external domain only) of a Scalar.
Implements Map.
Definition at line 581 of file map_radial_r_manip.C.
References Valeur::annule(), Valeur::base, Scalar::get_etat(), Valeur::get_mg(), Mg3d::get_nzone(), Scalar::get_spectral_va(), Mg3d::get_type_r(), Map::mg, Valeur::mult_xm1_zec(), Scalar::set_etat_qcq(), Scalar::set_spectral_va(), and xsr.
| void Map_radial::div_rsint | ( | Scalar & | ci | ) | const [virtual] |
Division by 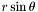 of a
of a Scalar.
Implements Map.
Definition at line 430 of file map_radial_r_manip.C.
References Scalar::annule(), Tensor::annule_domain(), Valeur::base, Scalar::get_etat(), Valeur::get_mg(), Mg3d::get_nzone(), Mg3d::get_type_r(), Map::mg, Valeur::mult_x(), Scalar::set_etat_qcq(), Scalar::set_spectral_va(), Valeur::ssint(), Valeur::sx(), and xsr.
| void Map_radial::div_sint | ( | Scalar & | ci | ) | const [virtual] |
Division by 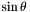 of a
of a Scalar.
Implements Map.
Definition at line 129 of file map_radial_th_manip.C.
References Scalar::get_etat(), Valeur::get_mg(), Map::mg, Scalar::set_etat_qcq(), Scalar::set_spectral_va(), and Valeur::ssint().
| void Map_radial::div_tant | ( | Scalar & | ci | ) | const [virtual] |
Division by 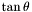 of a
of a Scalar.
Implements Map.
Definition at line 154 of file map_radial_th_manip.C.
References Scalar::get_etat(), Valeur::get_mg(), Map::mg, Valeur::mult_ct(), Scalar::set_etat_qcq(), Scalar::set_spectral_va(), and Valeur::ssint().
Function intended to be used by Map::poisson_vect and Map::poisson_vect_oohara .
It constructs the sets of parameters used for each scalar Poisson equation from the one for the vectorial one.
- Parameters:
-
para [input] : the Paramused for the resolution of the vectorial Poisson equation : \para.int()maximum number of iteration.\para.double(0)relaxation parameter.\para.double(1)required precision. \para.tenseur_mod()source of the vectorial part at the previous step.\para.cmp_mod()source of the scalar part at the previous step.i [input] number of the scalar Poisson equation that is being solved (values from 0 to 2 for the componants of the vectorial part and 3 for the scalar one).
- Returns:
- the pointer on the parameter set used for solving the scalar Poisson equation labelled by i .
Computes 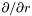 of a
of a Scalar if the description is affine and 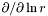 if it is logarithmic.
if it is logarithmic.
Note that in the compactified external domain (CED), the dzpuis flag of the output is 2 if the input has dzpuis = 0, and is increased by 1 in other cases.
- Parameters:
-
uu [input] field to consider resu [output] derivative of uu
| const Metric_flat & Map::flat_met_cart | ( | ) | const [inherited] |
Returns the flat metric associated with the Cartesian coordinates and with components expressed in the triad bvect_cart.
Definition at line 327 of file map.C.
References Map::bvect_cart, and Map::p_flat_met_cart.
| const Metric_flat & Map::flat_met_spher | ( | ) | const [inherited] |
Returns the flat metric associated with the spherical coordinates and with components expressed in the triad bvect_spher.
Definition at line 317 of file map.C.
References Map::bvect_spher, and Map::p_flat_met_spher.
| const Base_vect_cart& Map::get_bvect_cart | ( | ) | const [inline, inherited] |
Returns the Cartesian basis 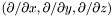 associated with the coordinates (x,y,z) of the mapping, i.e.
associated with the coordinates (x,y,z) of the mapping, i.e.
the Cartesian coordinates related to 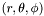 by means of usual formulae.
by means of usual formulae.
Definition at line 787 of file map.h.
References Map::bvect_cart.
| const Base_vect_spher& Map::get_bvect_spher | ( | ) | const [inline, inherited] |
Returns the orthonormal vectorial basis 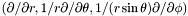 associated with the coordinates
associated with the coordinates 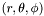 of the mapping.
of the mapping.
Definition at line 779 of file map.h.
References Map::bvect_spher.
| const Mg3d* Map::get_mg | ( | ) | const [inline, inherited] |
| double Map::get_ori_x | ( | ) | const [inline, inherited] |
Returns the x coordinate of the origin.
Definition at line 764 of file map.h.
References Map::ori_x.
| double Map::get_ori_y | ( | ) | const [inline, inherited] |
Returns the y coordinate of the origin.
Definition at line 766 of file map.h.
References Map::ori_y.
| double Map::get_ori_z | ( | ) | const [inline, inherited] |
Returns the z coordinate of the origin.
Definition at line 768 of file map.h.
References Map::ori_z.
| double Map::get_rot_phi | ( | ) | const [inline, inherited] |
Returns the angle between the x --axis and X --axis.
Definition at line 771 of file map.h.
References Map::rot_phi.
| virtual void Map::homothetie | ( | double | lambda | ) | [pure virtual, inherited] |
| void Map_radial::inc2_dzpuis | ( | Scalar & | ci | ) | const [virtual] |
Increases by 2 the value of dzpuis of a Scalar and changes accordingly its values in the compactified external domain (CED).
Implements Map.
Definition at line 795 of file map_radial_r_manip.C.
References Valeur::annule(), Scalar::get_dzpuis(), Scalar::get_etat(), Valeur::get_mg(), Mg3d::get_nzone(), Mg3d::get_type_r(), Map::mg, Scalar::set_dzpuis(), Scalar::set_etat_qcq(), Scalar::set_spectral_va(), and xsr.
| void Map_radial::inc_dzpuis | ( | Scalar & | ci | ) | const [virtual] |
Increases by 1 the value of dzpuis of a Scalar and changes accordingly its values in the compactified external domain (CED).
Implements Map.
Definition at line 692 of file map_radial_r_manip.C.
References Valeur::annule(), Scalar::get_dzpuis(), Scalar::get_etat(), Valeur::get_mg(), Mg3d::get_nzone(), Mg3d::get_type_r(), Map::mg, Scalar::set_dzpuis(), Scalar::set_etat_qcq(), Scalar::set_spectral_va(), and xsr.
| virtual void Map::laplacien | ( | const Scalar & | uu, | |
| int | zec_mult_r, | |||
| Scalar & | lap | |||
| ) | const [pure virtual, inherited] |
Computes the Laplacian of a scalar field.
| virtual const Map_af& Map::mp_angu | ( | int | ) | const [pure virtual, inherited] |
| void Map_radial::mult_cost | ( | Scalar & | ci | ) | const [virtual] |
Multiplication by 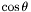 of a
of a Scalar.
Implements Map.
Definition at line 57 of file map_radial_th_manip.C.
References Scalar::get_etat(), Valeur::get_mg(), Map::mg, Valeur::mult_ct(), Scalar::set_etat_qcq(), and Scalar::set_spectral_va().
| void Map_radial::mult_r | ( | Cmp & | ci | ) | const [virtual] |
Multiplication by r of a Cmp.
In the CED, there is only a decrement of dzpuis
Implements Map.
Definition at line 215 of file map_radial_r_manip.C.
References Cmp::annule(), Valeur::base, Cmp::get_dzpuis(), Cmp::get_etat(), Valeur::get_mg(), Mg3d::get_nzone(), Mg3d::get_type_r(), Map::mg, Valeur::mult_x(), Cmp::set_dzpuis(), Cmp::va, and xsr.
| void Map_radial::mult_r | ( | Scalar & | uu | ) | const [virtual] |
Multiplication by r of a Scalar, the dzpuis of uu is not changed.
Implements Map.
Definition at line 140 of file map_radial_r_manip.C.
References Scalar::annule(), Tensor::annule_domain(), Valeur::base, Scalar::get_etat(), Valeur::get_mg(), Mg3d::get_nzone(), Mg3d::get_type_r(), Map::mg, Valeur::mult_x(), Scalar::set_etat_qcq(), Scalar::set_spectral_va(), Valeur::sxm1_zec(), and xsr.
| void Map_radial::mult_r_zec | ( | Scalar & | ci | ) | const [virtual] |
Multiplication by r (in the compactified external domain only) of a Scalar.
Implements Map.
Definition at line 292 of file map_radial_r_manip.C.
References Valeur::annule(), Valeur::base, Scalar::get_etat(), Valeur::get_mg(), Mg3d::get_nzone(), Mg3d::get_type_r(), Map::mg, Scalar::set_etat_qcq(), Scalar::set_spectral_va(), Valeur::sxm1_zec(), and xsr.
| void Map_radial::mult_rsint | ( | Scalar & | ci | ) | const [virtual] |
Multiplication by 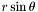 of a
of a Scalar.
Implements Map.
Definition at line 351 of file map_radial_r_manip.C.
References Scalar::annule(), Tensor::annule_domain(), Valeur::base, Scalar::get_etat(), Valeur::get_mg(), Mg3d::get_nzone(), Mg3d::get_type_r(), Map::mg, Valeur::mult_st(), Valeur::mult_x(), Scalar::set_etat_qcq(), Scalar::set_spectral_va(), Valeur::sxm1_zec(), and xsr.
| void Map_radial::mult_sint | ( | Scalar & | ci | ) | const [virtual] |
Multiplication by 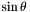 of a
of a Scalar.
Implements Map.
Definition at line 105 of file map_radial_th_manip.C.
References Scalar::get_etat(), Valeur::get_mg(), Map::mg, Valeur::mult_st(), Scalar::set_etat_qcq(), and Scalar::set_spectral_va().
| virtual void Map_radial::operator= | ( | const Map_af & | ) | [pure virtual] |
| virtual bool Map::operator== | ( | const Map & | ) | const [pure virtual, inherited] |
Comparison operator (egality).
| virtual bool Map_radial::operator== | ( | const Map & | ) | const [pure virtual] |
| virtual void Map::poisson | ( | const Cmp & | source, | |
| Param & | par, | |||
| Cmp & | uu | |||
| ) | const [pure virtual, inherited] |
Computes the solution of a scalar Poisson equation.
- Parameters:
-
source [input] source  of the Poisson equation
of the Poisson equation 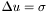 .
. par [input/output] possible parameters to control the resolution of the Poisson equation. See the actual implementation in the derived class of Mapfor documentation.uu [input/output] solution u with the boundary condition u =0 at spatial infinity.
| virtual void Map::poisson2d | ( | const Cmp & | source_mat, | |
| const Cmp & | source_quad, | |||
| Param & | par, | |||
| Cmp & | uu | |||
| ) | const [pure virtual, inherited] |
Computes the solution of a 2-D Poisson equation.
The 2-D Poisson equation writes
![\[ {\partial^2 u\over\partial r^2} + {1\over r} {\partial u \over \partial r} + {1\over r^2} {\partial^2 u\over\partial \theta^2} = \sigma \ . \]](form_512.png)
- Parameters:
-
source_mat [input] Compactly supported part of the source  of the 2-D Poisson equation (typically matter terms)
of the 2-D Poisson equation (typically matter terms) source_quad [input] Non-compactly supported part of the source  of the 2-D Poisson equation (typically quadratic terms)
of the 2-D Poisson equation (typically quadratic terms) par [input/output] possible parameters to control the resolution of the Poisson equation. See the actual implementation in the derived class of Mapfor documentation.uu [input/output] solution u with the boundary condition u =0 at spatial infinity.
| virtual void Map::poisson_angu | ( | const Scalar & | source, | |
| Param & | par, | |||
| Scalar & | uu, | |||
| double | lambda = 0 | |||
| ) | const [pure virtual, inherited] |
Computes the solution of the generalized angular Poisson equation.
The generalized angular Poisson equation is 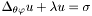 , where
, where 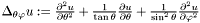 .
.
- Parameters:
-
source [input] source  of the equation
of the equation 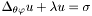 .
. par [input/output] possible parameters to control the resolution of the Poisson equation. See the actual implementation in the derived class of Mapfor documentation.uu [input/output] solution u lambda [input] coefficient 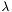 in the above equation (default value = 0)
in the above equation (default value = 0)
| void Map_radial::poisson_compact | ( | int | nzet, | |
| const Cmp & | source, | |||
| const Cmp & | aa, | |||
| const Tenseur & | bb, | |||
| const Param & | par, | |||
| Cmp & | psi | |||
| ) | const [virtual] |
Resolution of the elliptic equation 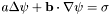 in the case of a multidomain stellar interior.
in the case of a multidomain stellar interior.
- Parameters:
-
nzet [input] number of domains covering the stellar interior source [input] source  of the above equation
of the above equation aa [input] factor a in the above equation bb [input] vector b in the above equation par [input/output] possible parameters to control the resolution of the equation. See the actual implementation in the derived class of Mapfor documentation.psi [input/output] solution 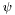 which satisfies
which satisfies 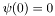 .
.
Implements Map.
Definition at line 449 of file map_radial_poisson_cpt.C.
References Cmp::annule(), Mtbl::annule_hard(), Tbl::annule_hard(), Map::bvect_spher, Valeur::c_cf, Valeur::coef(), diffrel(), Map_af::dsdr(), Cmp::dsdr(), Param::get_double(), Tenseur::get_etat(), Cmp::get_etat(), Mg3d::get_grille3d(), Param::get_int(), Param::get_int_mod(), Tenseur::get_mp(), Cmp::get_mp(), Mg3d::get_np(), Mg3d::get_nr(), Mg3d::get_nt(), Mg3d::get_nzone(), Tenseur::get_triad(), Cmp::laplacien(), Map_af::laplacien(), max(), Map::mg, min(), poisson_compact(), Mtbl::set(), Tbl::set(), Cmp::set_etat_qcq(), Cmp::set_etat_zero(), Cmp::srdsdt(), Cmp::srstdsdp(), Valeur::std_base_scal(), Tbl::t, Cmp::va, Grille3d::x, Valeur::ylm(), and Valeur::ylm_i().
| void Map_radial::poisson_compact | ( | const Cmp & | source, | |
| const Cmp & | aa, | |||
| const Tenseur & | bb, | |||
| const Param & | par, | |||
| Cmp & | psi | |||
| ) | const [virtual] |
Resolution of the elliptic equation 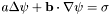 in the case where the stellar interior is covered by a single domain.
in the case where the stellar interior is covered by a single domain.
- Parameters:
-
source [input] source  of the above equation
of the above equation aa [input] factor a in the above equation bb [input] vector b in the above equation par [input/output] parameters of the iterative method of resolution : \ par.get_int(0): [input] maximum number of iterations \par.get_double(0): [input] required precision: the iterative method is stopped as soon as the relative difference between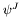 and
and 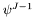 is greater than
is greater than par.get_double(0)\par.get_double(1): [input] relaxation parameter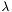 \
\ par.get_int_mod(0): [output] number of iterations actually used to get the solution.psi [input/output]: input : previously computed value of 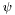 to start the iteration (if nothing is known a priori,
to start the iteration (if nothing is known a priori, psimust be set to zero); output: solution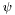 which satisfies
which satisfies 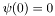 .
.
Implements Map.
Definition at line 151 of file map_radial_poisson_cpt.C.
References Cmp::annule(), Map::bvect_spher, Valeur::c_cf, Valeur::coef(), Valeur::d2sdx2(), diffrel(), Cmp::dsdr(), Valeur::dsdx(), dxdr, Param::get_double(), Tenseur::get_etat(), Cmp::get_etat(), Param::get_int(), Param::get_int_mod(), Tenseur::get_mp(), Cmp::get_mp(), Mg3d::get_nr(), Mg3d::get_nzone(), Tenseur::get_triad(), Valeur::lapang(), Cmp::laplacien(), max(), Map::mg, min(), Valeur::mult_x(), Cmp::set_etat_qcq(), Cmp::set_etat_zero(), Cmp::srdsdt(), Cmp::srstdsdp(), Valeur::std_base_scal(), Valeur::sx(), Cmp::va, Valeur::ylm(), and Valeur::ylm_i().
| virtual void Map::poisson_frontiere | ( | const Cmp & | source, | |
| const Valeur & | limite, | |||
| int | raccord, | |||
| int | num_front, | |||
| Cmp & | pot, | |||
| double | = 0., |
|||
| double | = 0. | |||
| ) | const [pure virtual, inherited] |
Computes the solution of a Poisson equation from the domain num_front+1 .
imposing a boundary condition at the boundary between the domains num_front and num_front+1 .
- Parameters:
-
source [input] : source of the equation. limite [input] : limite[num_front] contains the angular function being the boudary condition.raccord [input] : 1 for the Dirichlet problem and 2 for the Neumann one and 3 for Dirichlet-Neumann. num_front [input] : index of the boudary at which the boundary condition has to be imposed. pot [output] : result. fact_dir [input] : Valeur by which we multiply the quantity we solve. (in the case of Dirichlet-Neumann boundary condition.) fact_neu [input] : Valeur by which we multiply the radial derivative of the quantity we solve. (in the case of Dirichlet-Neumann boundary condition.)
| virtual void Map::poisson_interne | ( | const Cmp & | source, | |
| const Valeur & | limite, | |||
| Param & | par, | |||
| Cmp & | pot | |||
| ) | const [pure virtual, inherited] |
Computes the solution of a Poisson equation in the shell, imposing a boundary condition at the surface of the star.
- Parameters:
-
source [input] : source of the equation. limite [input] : limite[num_front] contains the angular function being the boudary condition.par [input] : parameters of the computation. pot [output] : result.
| virtual void Map::poisson_regular | ( | const Cmp & | source, | |
| int | k_div, | |||
| int | nzet, | |||
| double | unsgam1, | |||
| Param & | par, | |||
| Cmp & | uu, | |||
| Cmp & | uu_regu, | |||
| Cmp & | uu_div, | |||
| Tenseur & | duu_div, | |||
| Cmp & | source_regu, | |||
| Cmp & | source_div | |||
| ) | const [pure virtual, inherited] |
Computes the solution of a scalar Poisson equation.
The regularized source
- Parameters:
-
source [input] source  of the Poisson equation
of the Poisson equation 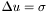 .
. k_div [input] regularization degree of the procedure nzet [input] number of domains covering the star unsgam1 [input] parameter 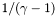 where
where  denotes the adiabatic index.
denotes the adiabatic index. par [input/output] possible parameters to control the resolution of the Poisson equation. See the actual implementation in the derived class of Mapfor documentation.uu [input/output] solution u with the boundary condition u =0 at spatial infinity. uu_regu [output] solution of the regular part of the source. uu_div [output] solution of the diverging part of the source. duu_div [output] derivative of the diverging potential source_regu [output] regularized source source_div [output] diverging part of the source
| virtual void Map::poisson_tau | ( | const Cmp & | source, | |
| Param & | par, | |||
| Cmp & | uu | |||
| ) | const [pure virtual, inherited] |
Computes the solution of a scalar Poisson equationwith a Tau method.
- Parameters:
-
source [input] source  of the Poisson equation
of the Poisson equation 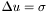 .
. par [input/output] possible parameters to control the resolution of the Poisson equation. See the actual implementation in the derived class of Mapfor documentation.uu [input/output] solution u with the boundary condition u =0 at spatial infinity.
| virtual void Map::primr | ( | const Scalar & | uu, | |
| Scalar & | resu, | |||
| bool | null_infty | |||
| ) | const [pure virtual, inherited] |
Computes the radial primitive which vanishes for 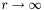 .
.
i.e. the function 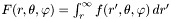
- Parameters:
-
uu [input] function f (must have a dzpuis= 2)resu [input] function F null_infty if true (default), the primitive is null at infinity (or on the grid boundary). F is null at the center otherwise
| virtual void Map::reevaluate | ( | const Map * | mp_prev, | |
| int | nzet, | |||
| Scalar & | uu | |||
| ) | const [pure virtual, inherited] |
Recomputes the values of a Scalar at the collocation points after a change in the mapping.
- Parameters:
-
mp_prev [input] Previous value of the mapping. nzet [input] Number of domains where the computation must be done: the computation is performed for the domains of index 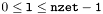 ;
; uuis set to zero in the other domains.uu [input/output] input : Scalarpreviously computed on the mapping*mp_prev; ouput : values of (logically) the sameScalaeat the grid points defined by*this.
| virtual void Map::reevaluate | ( | const Map * | mp_prev, | |
| int | nzet, | |||
| Cmp & | uu | |||
| ) | const [pure virtual, inherited] |
Recomputes the values of a Cmp at the collocation points after a change in the mapping.
- Parameters:
-
mp_prev [input] Previous value of the mapping. nzet [input] Number of domains where the computation must be done: the computation is performed for the domains of index 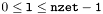 ;
; uuis set to zero in the other domains.uu [input/output] input : Cmppreviously computed on the mapping*mp_prev; ouput : values of (logically) the sameCmpat the grid points defined by*this.
Recomputes the values of a Scalar at the collocation points after a change in the mapping.
- Parameters:
-
mp_prev [input] Previous value of the mapping. nzet [input] Number of domains where the computation must be done: the computation is performed for the domains of index 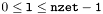 ;
; uuis set to zero in the other domains.uu [input/output] input : Scalarpreviously computed on the mapping*mp_prev; ouput : values of (logically) the sameScalarat the grid points defined by*this.
Definition at line 169 of file map_radial_reevaluate.C.
References Param::add_double(), Param::add_int(), Param::add_int_mod(), Scalar::annule(), Coord::c, Valeur::c, Valeur::c_cf, Valeur::coef(), Coord::fait(), Scalar::get_dzpuis(), Scalar::get_etat(), Tensor::get_mp(), Mg3d::get_np(), Mg3d::get_nr(), Mg3d::get_nt(), Mg3d::get_nzone(), Map::mg, Map::r, Valeur::set_etat_c_qcq(), Tbl::set_etat_qcq(), Mtbl::set_etat_qcq(), Scalar::set_spectral_va(), Mtbl::t, val_lx_jk(), and Mtbl_cf::val_point_jk().
Recomputes the values of a Cmp at the collocation points after a change in the mapping.
- Parameters:
-
mp_prev [input] Previous value of the mapping. nzet [input] Number of domains where the computation must be done: the computation is performed for the domains of index 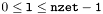 ;
; uuis set to zero in the other domains.uu [input/output] input : Cmppreviously computed on the mapping*mp_prev; ouput : values of (logically) the sameCmpat the grid points defined by*this.
Definition at line 54 of file map_radial_reevaluate.C.
References Param::add_double(), Param::add_int(), Param::add_int_mod(), Cmp::annule(), Coord::c, Coord::fait(), Cmp::get_dzpuis(), Cmp::get_etat(), Cmp::get_mp(), Mg3d::get_np(), Mg3d::get_nr(), Mg3d::get_nt(), Mg3d::get_nzone(), Map::mg, Map::r, Tbl::set_etat_qcq(), Mtbl::set_etat_qcq(), Mtbl::t, Cmp::va, val_lx_jk(), and Mtbl_cf::val_point_jk().
| virtual void Map::reevaluate_symy | ( | const Map * | mp_prev, | |
| int | nzet, | |||
| Scalar & | uu | |||
| ) | const [pure virtual, inherited] |
Recomputes the values of a Scalar at the collocation points after a change in the mapping.
Case where the Scalar is symmetric with respect the plane y=0.
- Parameters:
-
mp_prev [input] Previous value of the mapping. nzet [input] Number of domains where the computation must be done: the computation is performed for the domains of index 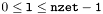 ;
; uuis set to zero in the other domains.uu [input/output] input : Scalarpreviously computed on the mapping*mp_prev; ouput : values of (logically) the sameScalarat the grid points defined by*this.
| virtual void Map::reevaluate_symy | ( | const Map * | mp_prev, | |
| int | nzet, | |||
| Cmp & | uu | |||
| ) | const [pure virtual, inherited] |
Recomputes the values of a Cmp at the collocation points after a change in the mapping.
Case where the Cmp is symmetric with respect the plane y=0.
- Parameters:
-
mp_prev [input] Previous value of the mapping. nzet [input] Number of domains where the computation must be done: the computation is performed for the domains of index 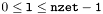 ;
; uuis set to zero in the other domains.uu [input/output] input : Cmppreviously computed on the mapping*mp_prev; ouput : values of (logically) the sameCmpat the grid points defined by*this.
Recomputes the values of a Scalar at the collocation points after a change in the mapping.
Case where the Scalar is symmetric with respect to the plane y=0.
- Parameters:
-
mp_prev [input] Previous value of the mapping. nzet [input] Number of domains where the computation must be done: the computation is performed for the domains of index 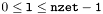 ;
; uuis set to zero in the other domains.uu [input/output] input : Scalarpreviously computed on the mapping*mp_prev; ouput : values of (logically) the sameScalarat the grid points defined by*this.
Definition at line 189 of file map_radial_reeval_symy.C.
References Param::add_double(), Param::add_int(), Param::add_int_mod(), Scalar::annule(), Coord::c, Valeur::c, Valeur::c_cf, Valeur::coef(), Coord::fait(), Scalar::get_dzpuis(), Scalar::get_etat(), Tensor::get_mp(), Mg3d::get_np(), Mg3d::get_nr(), Mg3d::get_nt(), Mg3d::get_nzone(), Mg3d::get_type_p(), Map::mg, Map::r, Valeur::set_etat_c_qcq(), Tbl::set_etat_qcq(), Mtbl::set_etat_qcq(), Scalar::set_spectral_va(), Mtbl::t, val_lx_jk(), and Mtbl_cf::val_point_jk_symy().
Recomputes the values of a Cmp at the collocation points after a change in the mapping.
Case where the Cmp is symmetric with respect to the plane y=0.
- Parameters:
-
mp_prev [input] Previous value of the mapping. nzet [input] Number of domains where the computation must be done: the computation is performed for the domains of index 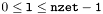 ;
; uuis set to zero in the other domains.uu [input/output] input : Cmppreviously computed on the mapping*mp_prev; ouput : values of (logically) the sameCmpat the grid points defined by*this.
Definition at line 55 of file map_radial_reeval_symy.C.
References Param::add_double(), Param::add_int(), Param::add_int_mod(), Cmp::annule(), Coord::c, Coord::fait(), Cmp::get_dzpuis(), Cmp::get_etat(), Cmp::get_mp(), Mg3d::get_np(), Mg3d::get_nr(), Mg3d::get_nt(), Mg3d::get_nzone(), Mg3d::get_type_p(), Map::mg, Map::r, Tbl::set_etat_qcq(), Mtbl::set_etat_qcq(), Mtbl::t, Cmp::va, val_lx_jk(), and Mtbl_cf::val_point_jk_symy().
| void Map_radial::reset_coord | ( | ) | [protected, virtual] |
| virtual void Map::resize | ( | int | l, | |
| double | lambda | |||
| ) | [pure virtual, inherited] |
Rescales the outer boundary of one domain.
The inner boundary is unchanged. The inner boundary of the next domain is changed to match the new outer boundary.
- Parameters:
-
l [input] index of the domain lambda [input] factor by which the value of 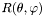 defining the outer boundary of the domain is to be multiplied.
defining the outer boundary of the domain is to be multiplied.
| void Map_radial::sauve | ( | FILE * | fd | ) | const [virtual] |
| void Map::set_ori | ( | double | xa0, | |
| double | ya0, | |||
| double | za0 | |||
| ) | [inherited] |
Sets a new origin.
Definition at line 249 of file map.C.
References Map::bvect_spher, Map::ori_x, Map::ori_y, Map::ori_z, Map::reset_coord(), and Base_vect_spher::set_ori().
| void Map::set_rot_phi | ( | double | phi0 | ) | [inherited] |
Sets a new rotation angle.
Definition at line 259 of file map.C.
References Map::bvect_cart, Map::bvect_spher, Map::reset_coord(), Map::rot_phi, Base_vect_cart::set_rot_phi(), and Base_vect_spher::set_rot_phi().
| virtual void Map::val_lx | ( | double | rr, | |
| double | theta, | |||
| double | pphi, | |||
| const Param & | par, | |||
| int & | l, | |||
| double & | xi | |||
| ) | const [pure virtual, inherited] |
Computes the domain index l and the value of  corresponding to a point given by its physical coordinates
corresponding to a point given by its physical coordinates 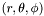 .
.
This version enables to pass some parameters to control the accuracy of the computation.
- Parameters:
-
rr [input] value of r theta [input] value of 
pphi [input] value of 
par [input/output] parameters to control the accuracy of the computation l [output] value of the domain index xi [output] value of 
| virtual void Map::val_lx | ( | double | rr, | |
| double | theta, | |||
| double | pphi, | |||
| int & | l, | |||
| double & | xi | |||
| ) | const [pure virtual, inherited] |
| virtual void Map_radial::val_lx_jk | ( | double | rr, | |
| int | j, | |||
| int | k, | |||
| const Param & | par, | |||
| int & | l, | |||
| double & | xi | |||
| ) | const [pure virtual] |
Computes the domain index l and the value of  corresponding to a point of arbitrary r but collocation values of
corresponding to a point of arbitrary r but collocation values of 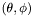 .
.
- Parameters:
-
rr [input] value of r j [input] index of the collocation point in 
k [input] index of the collocation point in 
par [input/output] parameters to control the accuracy of the computation l [output] value of the domain index xi [output] value of 
| virtual double Map::val_r | ( | int | l, | |
| double | xi, | |||
| double | theta, | |||
| double | pphi | |||
| ) | const [pure virtual, inherited] |
| virtual double Map_radial::val_r_jk | ( | int | l, | |
| double | xi, | |||
| int | j, | |||
| int | k | |||
| ) | const [pure virtual] |
Returns the value of the radial coordinate r for a given  and a given collocation point in
and a given collocation point in 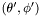 in a given domain.
in a given domain.
- Parameters:
-
l [input] index of the domain xi [input] value of 
j [input] index of the collocation point in 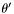
k [input] index of the collocation point in 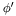
- Returns:
- value of
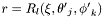
Friends And Related Function Documentation
| ostream& operator<< | ( | ostream & | , | |
| const Map & | ||||
| ) | [friend, inherited] |
Operator <<.
Member Data Documentation
Base_vect_cart Map::bvect_cart [protected, inherited] |
Base_vect_spher Map::bvect_spher [protected, inherited] |
double Map::ori_x [protected, inherited] |
double Map::ori_y [protected, inherited] |
double Map::ori_z [protected, inherited] |
Cmp* Map::p_cmp_zero [protected, inherited] |
Metric_flat* Map::p_flat_met_cart [mutable, protected, inherited] |
Metric_flat* Map::p_flat_met_spher [mutable, protected, inherited] |
Map_af* Map::p_mp_angu [mutable, protected, inherited] |
double Map::rot_phi [protected, inherited] |
The documentation for this class was generated from the following files:
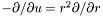 .
. 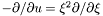 .
. 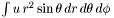 . The routine allocates a
. The routine allocates a 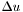 of which is to be computed
of which is to be computed 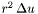 \ zec_mult_r = 4 (default) :
\ zec_mult_r = 4 (default) : 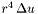
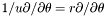 .
. 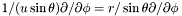 .
. 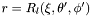
 1.6.1
1.6.1