Transverse and traceless symmetric tensors of rank 2. More...
#include <sym_tensor.h>
Public Member Functions | |
| Sym_tensor_tt (const Map &map, const Base_vect &triad_i, const Metric &met) | |
| Standard constructor. More... | |
| Sym_tensor_tt (const Sym_tensor_tt &) | |
| Copy constructor. More... | |
| Sym_tensor_tt (const Map &map, const Base_vect &triad_i, const Metric &met, FILE *fich) | |
Constructor from a file (see Tensor::sauve(FILE*) ). More... | |
| virtual | ~Sym_tensor_tt () |
| Destructor. More... | |
| virtual void | operator= (const Sym_tensor_tt &a) |
Assignment to another Sym_tensor_tt. More... | |
| virtual void | operator= (const Sym_tensor_trans &a) |
Assignment to a Sym_tensor_trans. More... | |
| virtual void | operator= (const Sym_tensor &a) |
Assignment to a Sym_tensor. More... | |
| virtual void | operator= (const Tensor_sym &a) |
Assignment to a Tensor_sym. More... | |
| virtual void | operator= (const Tensor &a) |
Assignment to a Tensor. More... | |
| void | set_rr_eta_mu (const Scalar &hrr, const Scalar &eta_i, const Scalar &mu_i) |
Sets the component 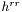 , as well as the angular potentials , as well as the angular potentials  and and  (see members (see members p_eta and p_mu ). More... | |
| void | set_rr_mu (const Scalar &hrr, const Scalar &mu_i) |
Sets the component 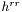 , as well as the angular potential , as well as the angular potential  (see member (see member p_mu ). More... | |
| void | set_khi_eta_mu (const Scalar &khi_i, const Scalar &eta_i, const Scalar &mu_i) |
Sets the component 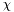 , as well as the angular potentials , as well as the angular potentials  and and  (see members (see members p_khi , p_eta and p_mu ). More... | |
| void | set_khi_mu (const Scalar &khi_i, const Scalar &mu_i, int dzp=0, Param *par1=0x0, Param *par2=0x0, Param *par3=0x0) |
Sets the component 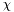 , as well as the angular potential , as well as the angular potential  (see member (see member p_khi and p_mu ). More... | |
| void | set_A_tildeB (const Scalar &a_in, const Scalar &tb_in, Param *par_bc=0x0, Param *par_mat=0x0) |
Assigns the derived members A and 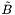 . More... . More... | |
| const Scalar & | khi () const |
Gives the field 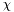 such that the component such that the component 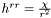 . More... . More... | |
| virtual const Scalar & | eta (Param *par=0x0) const |
Gives the field  (see member (see member p_eta ). More... | |
| Sym_tensor_tt | poisson (int dzfin=2) const |
Computes the solution of a tensorial TT Poisson equation with *this 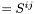 as a source: as a source:
. More... | |
| const Metric & | get_met_div () const |
| Returns the metric with respect to which the divergence and the trace are defined. More... | |
| void | set_tt_trace (const Sym_tensor_tt &a, const Scalar &h, Param *par=0x0) |
Assigns the derived members p_tt and p_trace and updates the components accordingly. More... | |
| const Scalar & | the_trace () const |
Returns the trace of the tensor with respect to metric *met_div. More... | |
| const Sym_tensor_tt & | tt_part (Param *par=0x0) const |
Returns the transverse traceless part of the tensor, the trace being defined with respect to metric *met_div. More... | |
| void | sol_Dirac_Abound (const Scalar &aaa, Scalar &tilde_mu, Scalar &x_new, Scalar bound_mu, const Param *par_bc) |
| Same resolution as sol_Dirac_A, but with inner boundary conditions added. More... | |
| void | sol_Dirac_A2 (const Scalar &aaa, Scalar &tilde_mu, Scalar &x_new, Scalar bound_mu, const Param *par_bc) |
| Same resolution as sol_Dirac_Abound, but here the boundary conditions are the degenerate elliptic conditions encontered when solving the Kerr problem. More... | |
| void | sol_Dirac_BC2 (const Scalar &bb, const Scalar &cc, const Scalar &hh, Scalar &hrr, Scalar &tilde_eta, Scalar &ww, Scalar bound_eta, double dir, double neum, double rhor, Param *par_bc, Param *par_mat) |
| Same resolution as sol_Dirac_tilde_B, but with inner boundary conditions added. More... | |
| void | sol_Dirac_BC3 (const Scalar &bb, const Scalar &hh, Scalar &hrr, Scalar &tilde_eta, Scalar &ww, Scalar bound_hrr, Scalar bound_eta, Param *par_bc, Param *par_mat) |
| Same resolution as sol_Dirac_Abound, but here the boundary conditions are the degenerate elliptic conditions encontered when solving the Kerr problem. More... | |
| void | sol_Dirac_l01_bound (const Scalar &hh, Scalar &hrr, Scalar &tilde_eta, Scalar &bound_hrr, Scalar &bound_eta, Param *par_mat) |
| void | sol_Dirac_l01_2 (const Scalar &hh, Scalar &hrr, Scalar &tilde_eta, Param *par_mat) |
| void | trace_from_det_one (const Sym_tensor_tt &htt, double precis=1.e-14, int it_max=100) |
Assigns the derived member p_tt and computes the trace so that *this + the flat metric has a determinant equal to 1. More... | |
| void | set_hrr_mu_det_one (const Scalar &hrr, const Scalar &mu_in, double precis=1.e-14, int it_max=100) |
Assigns the rr component and the derived member  . More... . More... | |
| void | set_tt_part_det_one (const Sym_tensor_tt &hijtt, const Scalar *h_prev=0x0, Param *par_mat=0x0, double precis=1.e-14, int it_max=100) |
| Assignes the TT-part of the tensor. More... | |
| void | set_AtBtt_det_one (const Scalar &a_in, const Scalar &tbtt_in, const Scalar *h_prev=0x0, Param *par_bc=0x0, Param *par_mat=0x0, double precis=1.e-14, int it_max=100) |
Assigns the derived member A and computes 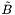 from its TT-part (see from its TT-part (see Sym_tensor::compute_tilde_B_tt() ). More... | |
| void | set_AtB_trace (const Scalar &a_in, const Scalar &tb_in, const Scalar &trace, Param *par_bc=0x0, Param *par_mat=0x0) |
Assigns the derived members A , 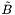 and the trace. More... and the trace. More... | |
| Sym_tensor_trans | poisson (const Scalar *h_guess=0x0) const |
Computes the solution of a tensorial transverse Poisson equation with *this 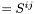 as a source: as a source:
In particular, it makes an iteration on the trace of the result, using | |
| void | set_longit_trans (const Vector &v, const Sym_tensor_trans &a) |
Assigns the derived members p_longit_pot and p_transverse and updates the components accordingly. More... | |
| void | set_auxiliary (const Scalar &trr, const Scalar &eta_over_r, const Scalar &mu_over_r, const Scalar &www, const Scalar &xxx, const Scalar &ttt) |
Assigns the component 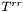 and the derived members and the derived members p_eta , p_mu , p_www, p_xxx and p_ttt , fro, their values and 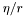 , , 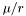 . More... . More... | |
| virtual void | exponential_filter_r (int lzmin, int lzmax, int p, double alpha=-16.) |
Applies exponential filters to all components (see Scalar::exponential_filter_r ). More... | |
| virtual void | exponential_filter_ylm (int lzmin, int lzmax, int p, double alpha=-16.) |
Applies exponential filters to all components (see Scalar::exponential_filter_ylm ). More... | |
| const Vector & | divergence (const Metric &) const |
Returns the divergence of this with respect to a Metric . More... | |
| Sym_tensor | derive_lie (const Vector &v) const |
Computes the Lie derivative of this with respect to some vector field v. More... | |
| const Sym_tensor_trans & | transverse (const Metric &gam, Param *par=0x0, int method_poisson=6) const |
Computes the transverse part 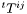 of the tensor with respect to a given metric, transverse meaning divergence-free with respect to that metric. More... of the tensor with respect to a given metric, transverse meaning divergence-free with respect to that metric. More... | |
| const Vector & | longit_pot (const Metric &gam, Param *par=0x0, int method_poisson=6) const |
Computes the vector potential 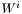 of longitudinal part of the tensor (see documentation of method of longitudinal part of the tensor (see documentation of method transverse() above). More... | |
| const Scalar & | mu (Param *par=0x0) const |
Gives the field  (see member (see member p_mu ). More... | |
| const Scalar & | www () const |
Gives the field W (see member p_www ). More... | |
| const Scalar & | xxx () const |
Gives the field X (see member p_xxx ). More... | |
| const Scalar & | ttt () const |
Gives the field T (see member p_ttt ). More... | |
| const Scalar & | compute_A (bool output_ylm=true, Param *par=0x0) const |
Gives the field A (see member p_aaa ). More... | |
| const Scalar & | compute_tilde_B (bool output_ylm=true, Param *par=0x0) const |
Gives the field 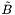 (see member (see member p_tilde_b ). More... | |
| Scalar | compute_tilde_B_tt (bool output_ylm=true, Param *par=0x0) const |
Gives the field 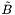 (see member (see member p_tilde_b ) associated with the TT-part of the Sym_tensor . More... | |
| const Scalar & | compute_tilde_C (bool output_ylm=true, Param *par=0x0) const |
Gives the field 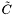 (see member (see member p_tilde_c ). More... | |
| int | sym_index1 () const |
Number of the first symmetric index (0<= id_sym1 < valence ) More... | |
| int | sym_index2 () const |
Number of the second symmetric index (id_sym1 < id_sym2 < valence ) More... | |
| virtual int | position (const Itbl &ind) const |
Returns the position in the array cmp of a component given by its indices. More... | |
| virtual Itbl | indices (int pos) const |
Returns the indices of a component given by its position in the array cmp . More... | |
| virtual void | sauve (FILE *) const |
| Save in a binary file. More... | |
| const Tensor_sym & | derive_cov (const Metric &gam) const |
Returns the covariant derivative of this with respect to some metric  . More... . More... | |
| const Tensor_sym & | derive_con (const Metric &gam) const |
Returns the "contravariant" derivative of this with respect to some metric  , by raising the last index of the covariant derivative (cf. More... , by raising the last index of the covariant derivative (cf. More... | |
| virtual void | set_etat_nondef () |
Sets the logical state of all components to ETATNONDEF (undefined state). More... | |
| virtual void | set_etat_zero () |
Sets the logical state of all components to ETATZERO (zero state). More... | |
| virtual void | set_etat_qcq () |
Sets the logical state of all components to ETATQCQ (ordinary state). More... | |
| virtual void | allocate_all () |
Performs the memory allocation of all the elements, down to the double arrays of the Tbl s. More... | |
| virtual void | change_triad (const Base_vect &new_triad) |
| Sets a new vectorial basis (triad) of decomposition and modifies the components accordingly. More... | |
| void | set_triad (const Base_vect &new_triad) |
| Assigns a new vectorial basis (triad) of decomposition. More... | |
| Scalar & | set (const Itbl &ind) |
| Returns the value of a component (read/write version). More... | |
| Scalar & | set (int i1, int i2) |
| Returns the value of a component for a tensor of valence 2 (read/write version). More... | |
| Scalar & | set (int i1, int i2, int i3) |
| Returns the value of a component for a tensor of valence 3 (read/write version). More... | |
| Scalar & | set (int i1, int i2, int i3, int i4) |
| Returns the value of a component for a tensor of valence 4 (read/write version). More... | |
| void | annule_domain (int l) |
Sets the Tensor to zero in a given domain. More... | |
| virtual void | annule (int l_min, int l_max) |
Sets the Tensor to zero in several domains. More... | |
| void | annule_extern_cn (int l_0, int deg) |
| Performs a smooth (C^n) transition in a given domain to zero. More... | |
| virtual void | std_spectral_base () |
| Sets the standard spectal bases of decomposition for each component. More... | |
| virtual void | std_spectral_base_odd () |
| Sets the standard odd spectal bases of decomposition for each component. More... | |
| virtual void | dec_dzpuis (int dec=1) |
Decreases by dec units the value of dzpuis and changes accordingly the values in the compactified external domain (CED). More... | |
| virtual void | inc_dzpuis (int inc=1) |
Increases by inc units the value of dzpuis and changes accordingly the values in the compactified external domain (CED). More... | |
| virtual void | exponential_filter_ylm_phi (int lzmin, int lzmax, int p_r, int p_tet, int p_phi, double alpha=-16.) |
Applies exponential filters to all components (see Scalar::exponential_filter_ylm_phi ). More... | |
| void | copy_coefs_from_smaller_grid (const Tensor &tens_small_grid) |
Copies the content of the argument Tensor to this defined on a larger grid, with similar mappings. More... | |
| void | copy_coefs_from_larger_grid (const Tensor &tens_large_grid) |
Copies the content of the argument Tensor to this defined on a smaller grid, with similar mappings. More... | |
| Tensor | up (int ind, const Metric &gam) const |
Computes a new tensor by raising an index of *this. More... | |
| Tensor | down (int ind, const Metric &gam) const |
Computes a new tensor by lowering an index of *this. More... | |
| Tensor | up_down (const Metric &gam) const |
Computes a new tensor by raising or lowering all the indices of *this . More... | |
| Tensor | trace (int ind1, int ind2) const |
| Trace on two different type indices. More... | |
| Tensor | trace (int ind1, int ind2, const Metric &gam) const |
| Trace with respect to a given metric. More... | |
| Scalar | trace () const |
| Trace on two different type indices for a valence 2 tensor. More... | |
| Scalar | trace (const Metric &gam) const |
| Trace with respect to a given metric for a valence 2 tensor. More... | |
| const Map & | get_mp () const |
| Returns the mapping. More... | |
| const Base_vect * | get_triad () const |
| Returns the vectorial basis (triad) on which the components are defined. More... | |
| int | get_valence () const |
| Returns the valence. More... | |
| int | get_n_comp () const |
| Returns the number of stored components. More... | |
| int | get_index_type (int i) const |
Gives the type (covariant or contravariant) of the index number i . More... | |
| Itbl | get_index_type () const |
| Returns the types of all the indices. More... | |
| int & | set_index_type (int i) |
Sets the type of the index number i . More... | |
| Itbl & | set_index_type () |
| Sets the types of all the indices. More... | |
| const Scalar & | operator() (const Itbl &ind) const |
| Returns the value of a component (read-only version). More... | |
| const Scalar & | operator() (int i1, int i2) const |
| Returns the value of a component for a tensor of valence 2 (read-only version). More... | |
| const Scalar & | operator() (int i1, int i2, int i3) const |
| Returns the value of a component for a tensor of valence 3 (read-only version). More... | |
| const Scalar & | operator() (int i1, int i2, int i3, int i4) const |
| Returns the value of a component for a tensor of valence 4 (read-only version). More... | |
| void | operator+= (const Tensor &) |
| += Tensor More... | |
| void | operator-= (const Tensor &) |
| -= Tensor More... | |
| virtual void | spectral_display (const char *comment=0x0, double threshold=1.e-7, int precision=4, ostream &ostr=cout) const |
| Displays the spectral coefficients and the associated basis functions of each component. More... | |
Protected Member Functions | |
| virtual void | del_deriv () const |
| Deletes the derived quantities. More... | |
| void | set_der_0x0 () const |
| Sets the pointers on derived quantities to 0x0. More... | |
| void | update (int dzp, Param *par1=0x0, Param *par2=0x0) |
Computes the components 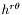 , , 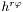 , , 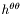 , , 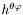 and and 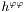 , from , from 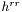 and the potentials and the potentials  and and  . More... . More... | |
| void | sol_Dirac_A (const Scalar &aaa, Scalar &tilde_mu, Scalar &xxx, const Param *par_bc=0x0) const |
Solves a system of two coupled first-order PDEs obtained from the divergence-free condition (Dirac gauge) and the requirement that the potential A (see Sym_tensor::p_aaa ) has a given value. More... | |
| void | sol_Dirac_tilde_B (const Scalar &tilde_b, const Scalar &hh, Scalar &hrr, Scalar &tilde_eta, Scalar &www, Param *par_bc=0x0, Param *par_mat=0x0) const |
Solves a system of three coupled first-order PDEs obtained from divergence-free conditions (Dirac gauge) and the requirement that the potential 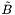 (see (see Sym_tensor::p_tilde_b ) has a given value. More... | |
| void | sol_Dirac_l01 (const Scalar &hh, Scalar &hrr, Scalar &tilde_eta, Param *par_mat) const |
Solves the same system as Sym_tensor_trans::sol_Dirac_tilde_B but only for 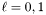 . More... . More... | |
| virtual void | del_derive_met (int i) const |
Logical destructor of the derivatives depending on the i-th element of met_depend specific to the class Sym_tensor (p_transverse , etc...). More... | |
| void | set_der_met_0x0 (int i) const |
Sets all the i-th components of met_depend specific to the class Sym_tensor (p_transverse , etc...) to 0x0. More... | |
| Scalar | get_tilde_B_from_TT_trace (const Scalar &tilde_B_tt_in, const Scalar &trace) const |
Computes 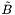 (see (see Sym_tensor::p_tilde_b ) from its transverse-traceless part and the trace. More... | |
| Sym_tensor * | inverse () const |
Returns a pointer on the inverse of the Sym_tensor (seen as a matrix). More... | |
| void | set_dependance (const Metric &) const |
To be used to describe the fact that the derivatives members have been calculated with met . More... | |
| int | get_place_met (const Metric &) const |
Returns the position of the pointer on metre in the array met_depend . More... | |
| void | compute_derive_lie (const Vector &v, Tensor &resu) const |
Computes the Lie derivative of this with respect to some vector field v (protected method; the public interface is method derive_lie ). More... | |
Protected Attributes | |
| Scalar * | p_khi |
Field 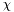 such that the component such that the component 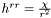 . More... . More... | |
| const Metric *const | met_div |
| Metric with respect to which the divergence and the trace are defined. More... | |
| Scalar * | p_trace |
Trace with respect to the metric *met_div. More... | |
| Sym_tensor_tt * | p_tt |
Traceless part with respect to the metric *met_div. More... | |
| Sym_tensor_trans * | p_transverse [N_MET_MAX] |
Array of the transverse part 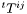 of the tensor with respect to various metrics, transverse meaning divergence-free with respect to a metric. More... of the tensor with respect to various metrics, transverse meaning divergence-free with respect to a metric. More... | |
| Vector * | p_longit_pot [N_MET_MAX] |
Array of the vector potential of the longitudinal part of the tensor with respect to various metrics (see documentation of member p_transverse. More... | |
| Scalar * | p_eta |
Field  such that the components such that the components 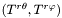 of the tensor are written (has only meaning with spherical components!): of the tensor are written (has only meaning with spherical components!):
. More... | |
| Scalar * | p_mu |
Field  such that the components such that the components 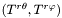 of the tensor are written (has only meaning with spherical components!): of the tensor are written (has only meaning with spherical components!):
. More... | |
| Scalar * | p_www |
Field W such that the components 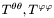 and and 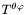 of the tensor are written (has only meaning with spherical components!): of the tensor are written (has only meaning with spherical components!):
. More... | |
| Scalar * | p_xxx |
Field X such that the components 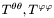 and and 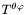 of the tensor are written (has only meaning with spherical components!): of the tensor are written (has only meaning with spherical components!):
. More... | |
| Scalar * | p_ttt |
Field T defined as 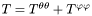 . More... . More... | |
| Scalar * | p_aaa |
Field A defined from X and  insensitive to the longitudinal part of the insensitive to the longitudinal part of the Sym_tensor (only for 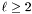 ). More... ). More... | |
| Scalar * | p_tilde_b |
Field 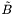 defined from defined from 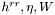 and h insensitive to the longitudinal part of the and h insensitive to the longitudinal part of the Sym_tensor. More... | |
| Scalar * | p_tilde_c |
Field 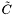 defined from defined from 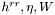 and h insensitive to the longitudinal part of the and h insensitive to the longitudinal part of the Sym_tensor. More... | |
| int | id_sym1 |
Number of the first symmetric index (0<= id_sym1 < valence ) More... | |
| int | id_sym2 |
Number of the second symmetric index (id_sym1 < id_sym2 < valence ) More... | |
| const Map *const | mp |
| Mapping on which the numerical values at the grid points are defined. More... | |
| int | valence |
| Valence of the tensor (0 = scalar, 1 = vector, etc...) More... | |
| const Base_vect * | triad |
| Vectorial basis (triad) with respect to which the tensor components are defined. More... | |
| Itbl | type_indice |
1D array of integers (class Itbl ) of size valence containing the type of each index: COV for a covariant one and CON for a contravariant one. More... | |
| int | n_comp |
| Number of stored components, depending on the symmetry. More... | |
| Scalar ** | cmp |
Array of size n_comp of pointers onto the components. More... | |
| const Metric * | met_depend [N_MET_MAX] |
Array on the Metric 's which were used to compute derived quantities, like p_derive_cov , etc... More... | |
| Tensor * | p_derive_cov [N_MET_MAX] |
Array of pointers on the covariant derivatives of this with respect to various metrics. More... | |
| Tensor * | p_derive_con [N_MET_MAX] |
Array of pointers on the contravariant derivatives of this with respect to various metrics. More... | |
| Tensor * | p_divergence [N_MET_MAX] |
Array of pointers on the divergence of this with respect to various metrics. More... | |
Detailed Description
Transverse and traceless symmetric tensors of rank 2.
This class is designed to store transverse (divergence-free) and transverse symmetric contravariant tensors of rank 2, with the component expressed in an orthonormal spherical basis 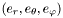 .()
.()
Definition at line 933 of file sym_tensor.h.
Constructor & Destructor Documentation
◆ Sym_tensor_tt() [1/3]
| Lorene::Sym_tensor_tt::Sym_tensor_tt | ( | const Map & | map, |
| const Base_vect & | triad_i, | ||
| const Metric & | met | ||
| ) |
Standard constructor.
- Parameters
-
map the mapping triad_i vectorial basis (triad) with respect to which the tensor components are defined met the metric with respect to which the divergence is defined
Definition at line 78 of file sym_tensor_tt.C.
References set_der_0x0().
◆ Sym_tensor_tt() [2/3]
| Lorene::Sym_tensor_tt::Sym_tensor_tt | ( | const Sym_tensor_tt & | source | ) |
Copy constructor.
Definition at line 88 of file sym_tensor_tt.C.
References p_khi, and set_der_0x0().
◆ Sym_tensor_tt() [3/3]
| Lorene::Sym_tensor_tt::Sym_tensor_tt | ( | const Map & | map, |
| const Base_vect & | triad_i, | ||
| const Metric & | met, | ||
| FILE * | fich | ||
| ) |
Constructor from a file (see Tensor::sauve(FILE*) ).
- Parameters
-
map the mapping triad_i vectorial basis (triad) with respect to which the tensor components are defined. It will be checked that it coincides with the basis saved in the file. met the metric with respect to which the divergence is defined fich file which has been used by the function sauve(FILE*).
Definition at line 100 of file sym_tensor_tt.C.
References set_der_0x0().
◆ ~Sym_tensor_tt()
|
virtual |
Member Function Documentation
◆ allocate_all()
|
virtualinherited |
Performs the memory allocation of all the elements, down to the double arrays of the Tbl s.
This function performs in fact recursive calls to set_etat_qcq() on each element of the chain Scalar -> Valeur -> Mtbl -> Tbl .
Reimplemented in Lorene::Scalar.
Definition at line 518 of file tensor.C.
References Lorene::Scalar::allocate_all(), Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), and Lorene::Tensor::n_comp.
◆ annule()
|
virtualinherited |
Sets the Tensor to zero in several domains.
- Parameters
-
l_min [input] The Tensorwill be set (logically) to zero in the domains whose indices are in the range[l_min,l_max] .l_max [input] see the comments for l_min.
Note that annule(0,nz-1) , where nz is the total number of domains, is equivalent to set_etat_zero() .
Reimplemented in Lorene::Scalar.
Definition at line 681 of file tensor.C.
References Lorene::Scalar::annule(), Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), Lorene::Map::get_mg(), Lorene::Mg3d::get_nzone(), Lorene::Tensor::mp, Lorene::Tensor::n_comp, and Lorene::Tensor::set_etat_zero().
◆ annule_domain()
|
inherited |
Sets the Tensor to zero in a given domain.
- Parameters
-
l [input] Index of the domain in which the Tensorwill be set (logically) to zero.
Definition at line 676 of file tensor.C.
References Lorene::Tensor::annule().
◆ annule_extern_cn()
|
inherited |
Performs a smooth (C^n) transition in a given domain to zero.
- Parameters
-
l_0 [input] in the domain of index l0 the tensor is multiplied by the right polynomial (of degree 2n+1), to ensure continuty of the function and its n first derivative at both ends of this domain. The tensor is unchanged in the domains l < l_0 and set to zero in domains l > l_0. deg [input] the degree n of smoothness of the transition.
Definition at line 700 of file tensor.C.
References Lorene::Map::get_mg(), Lorene::Mg3d::get_type_r(), and Lorene::Tensor::mp.
◆ change_triad()
|
virtualinherited |
Sets a new vectorial basis (triad) of decomposition and modifies the components accordingly.
Reimplemented in Lorene::Scalar, and Lorene::Vector.
Definition at line 80 of file tensor_change_triad.C.
References Lorene::Map::comp_p_from_cartesian(), Lorene::Map::comp_r_from_cartesian(), Lorene::Map::comp_t_from_cartesian(), Lorene::Map::comp_x_from_spherical(), Lorene::Map::comp_y_from_spherical(), Lorene::Map::comp_z_from_spherical(), Lorene::Base_vect_cart::get_align(), Lorene::Map::get_bvect_cart(), Lorene::Map::get_bvect_spher(), Lorene::Map::get_mg(), Lorene::Mg3d::get_np(), Lorene::Mg3d::get_nt(), Lorene::Mg3d::get_nzone(), Lorene::Tensor::mp, Lorene::Tensor::set(), Lorene::Tensor::triad, Lorene::Tensor::type_indice, and Lorene::Tensor::valence.
◆ compute_A()
|
inherited |
Gives the field A (see member p_aaa ).
- Parameters
-
output_ylm a flag to control the spectral decomposition base of the result: if true (default) the spherical harmonics base is used.
Definition at line 319 of file sym_tensor_aux.C.
References Lorene::Scalar::annule_l(), Lorene::Scalar::div_r_dzpuis(), Lorene::Scalar::div_tant(), Lorene::Scalar::dsdt(), Lorene::Scalar::get_dzpuis(), Lorene::Tensor::mp, Lorene::Tensor::operator()(), Lorene::Sym_tensor::p_aaa, Lorene::Map::poisson_angu(), Lorene::Scalar::poisson_angu(), Lorene::Scalar::set_spectral_va(), Lorene::Scalar::stdsdp(), Lorene::Tensor::triad, Lorene::Sym_tensor::xxx(), Lorene::Valeur::ylm(), and Lorene::Valeur::ylm_i().
◆ compute_derive_lie()
|
protectedinherited |
Computes the Lie derivative of this with respect to some vector field v (protected method; the public interface is method derive_lie ).
Definition at line 342 of file tensor_calculus.C.
References Lorene::Tensor::cmp, Lorene::contract(), Lorene::Scalar::dec_dzpuis(), Lorene::Tensor::derive_cov(), Lorene::Map::flat_met_cart(), Lorene::Map::flat_met_spher(), Lorene::Scalar::get_dzpuis(), Lorene::Tensor::get_n_comp(), Lorene::Tensor::get_triad(), Lorene::Tensor::indices(), Lorene::Tensor::mp, Lorene::Tensor::n_comp, Lorene::Tensor::operator()(), Lorene::Itbl::set(), Lorene::Tensor::set(), Lorene::Tensor::triad, Lorene::Tensor::type_indice, and Lorene::Tensor::valence.
◆ compute_tilde_B()
|
inherited |
Gives the field 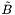 (see member
(see member p_tilde_b ).
- Parameters
-
output_ylm a flag to control the spectral decomposition base of the result: if true (default) the spherical harmonics base is used.
Definition at line 365 of file sym_tensor_aux.C.
References Lorene::Scalar::div_r_dzpuis(), Lorene::Scalar::div_tant(), Lorene::Scalar::dsdr(), Lorene::Scalar::dsdt(), Lorene::Scalar::get_dzpuis(), Lorene::Scalar::get_etat(), Lorene::Map::get_mg(), Lorene::Mg3d::get_nzone(), Lorene::Tensor::mp, Lorene::Tensor::operator()(), Lorene::Sym_tensor::p_tilde_b, Lorene::Map::poisson_angu(), Lorene::Scalar::poisson_angu(), Lorene::Scalar::set_etat_qcq(), Lorene::Scalar::set_spectral_va(), Lorene::Scalar::stdsdp(), Lorene::Tensor::triad, Lorene::Sym_tensor::ttt(), Lorene::Sym_tensor::www(), and Lorene::Valeur::ylm().
◆ compute_tilde_B_tt()
|
inherited |
Gives the field 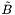 (see member
(see member p_tilde_b ) associated with the TT-part of the Sym_tensor .
- Parameters
-
output_ylm a flag to control the spectral decomposition base of the result: if true (default) the spherical harmonics base is used.
Definition at line 481 of file sym_tensor_aux.C.
References Lorene::Sym_tensor::compute_tilde_B(), and Lorene::Scalar::get_etat().
◆ compute_tilde_C()
|
inherited |
Gives the field 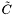 (see member
(see member p_tilde_c ).
- Parameters
-
output_ylm a flag to control the spectral decomposition base of the result: if true (default) the spherical harmonics base is used.
Definition at line 599 of file sym_tensor_aux.C.
References Lorene::Scalar::div_r_dzpuis(), Lorene::Scalar::div_tant(), Lorene::Scalar::dsdr(), Lorene::Scalar::dsdt(), Lorene::Scalar::get_dzpuis(), Lorene::Scalar::get_etat(), Lorene::Map::get_mg(), Lorene::Mg3d::get_nzone(), Lorene::Tensor::mp, Lorene::Tensor::operator()(), Lorene::Sym_tensor::p_tilde_c, Lorene::Map::poisson_angu(), Lorene::Scalar::poisson_angu(), Lorene::Scalar::set_etat_qcq(), Lorene::Scalar::set_spectral_va(), Lorene::Scalar::stdsdp(), Lorene::Tensor::triad, Lorene::Sym_tensor::ttt(), Lorene::Sym_tensor::www(), and Lorene::Valeur::ylm().
◆ copy_coefs_from_larger_grid()
|
inherited |
Copies the content of the argument Tensor to this defined on a smaller grid, with similar mappings.
It copies the coefficients, discarding the additional ones. Used for de-aliasing purposes.
- Parameters
-
tens_small_grid [input] Tensorto be copied, defined on the larger grid.
Definition at line 1123 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Scalar::copy_coefs_from_large_grid(), and Lorene::Tensor::n_comp.
◆ copy_coefs_from_smaller_grid()
|
inherited |
Copies the content of the argument Tensor to this defined on a larger grid, with similar mappings.
It copies the coefficients, setting the additional ones to zero. Used for de-aliasing purposes.
- Parameters
-
tens_small_grid [input] Tensorto be copied, defined on the smaller grid.
Definition at line 1116 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Scalar::copy_coefs_from_small_grid(), and Lorene::Tensor::n_comp.
◆ dec_dzpuis()
|
virtualinherited |
Decreases by dec units the value of dzpuis and changes accordingly the values in the compactified external domain (CED).
Reimplemented in Lorene::Scalar.
Definition at line 818 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), and Lorene::Tensor::n_comp.
◆ del_deriv()
|
protectedvirtual |
Deletes the derived quantities.
Reimplemented from Lorene::Sym_tensor_trans.
Definition at line 124 of file sym_tensor_tt.C.
References Lorene::Sym_tensor_trans::del_deriv(), p_khi, and set_der_0x0().
◆ del_derive_met()
|
protectedvirtualinherited |
Logical destructor of the derivatives depending on the i-th element of met_depend specific to the class Sym_tensor (p_transverse , etc...).
Reimplemented from Lorene::Tensor.
Definition at line 323 of file sym_tensor.C.
References Lorene::Tensor::del_derive_met(), Lorene::Tensor::met_depend, Lorene::Sym_tensor::p_longit_pot, Lorene::Sym_tensor::p_transverse, and Lorene::Sym_tensor::set_der_met_0x0().
◆ derive_con()
|
inherited |
Returns the "contravariant" derivative of this with respect to some metric  , by raising the last index of the covariant derivative (cf.
, by raising the last index of the covariant derivative (cf.
method derive_cov() ) with  .
.
Definition at line 207 of file tensor_sym_calculus.C.
References Lorene::Tensor::derive_con().
◆ derive_cov()
|
inherited |
Returns the covariant derivative of this with respect to some metric  .
.
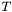 denoting the tensor represented by
denoting the tensor represented by this and 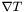 its covariant derivative with respect to the metric
its covariant derivative with respect to the metric  , the extra index (with respect to the indices of
, the extra index (with respect to the indices of 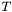 ) of
) of 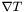 is chosen to be the last one. This convention agrees with that of MTW (see Eq. (10.17) of MTW).
is chosen to be the last one. This convention agrees with that of MTW (see Eq. (10.17) of MTW).
- Parameters
-
gam metric 
- Returns
- covariant derivative
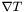 of
of thiswith respect to the connection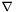 associated with the metric
associated with the metric 
Definition at line 195 of file tensor_sym_calculus.C.
References Lorene::Tensor::derive_cov().
◆ derive_lie()
|
inherited |
Computes the Lie derivative of this with respect to some vector field v.
Definition at line 363 of file sym_tensor.C.
References Lorene::Tensor::compute_derive_lie(), Lorene::Tensor::mp, Lorene::Tensor::triad, and Lorene::Tensor::type_indice.
◆ divergence()
Returns the divergence of this with respect to a Metric .
The indices are assumed to be contravariant.
Definition at line 352 of file sym_tensor.C.
References Lorene::Tensor::divergence().
◆ down()
Computes a new tensor by lowering an index of *this.
- Parameters
-
ind index to be lowered, with the following convention : ind1= 0 : first index of the tensorind1= 1 : second index of the tensor- and so on... (
indmust be of covariant type (CON)).
gam metric used to lower the index (contraction with the twice covariant form of the metric on the index ind).
Definition at line 268 of file tensor_calculus.C.
References Lorene::contract(), Lorene::Metric::cov(), Lorene::Tensor::indices(), Lorene::Tensor::mp, Lorene::Tensor::n_comp, Lorene::Itbl::set(), Lorene::Tensor::set(), Lorene::Tensor::triad, Lorene::Tensor::type_indice, and Lorene::Tensor::valence.
◆ eta()
Gives the field  (see member
(see member p_eta ).
Reimplemented from Lorene::Sym_tensor.
Definition at line 143 of file sym_tensor_tt_etamu.C.
References Lorene::Scalar::dec_dzpuis(), Lorene::Scalar::div_r_dzpuis(), Lorene::Scalar::dsdr(), Lorene::Scalar::get_dzpuis(), Lorene::Tensor::mp, Lorene::Scalar::mult_r_dzpuis(), Lorene::Tensor::operator()(), Lorene::Sym_tensor::p_eta, p_khi, Lorene::Map::poisson_angu(), Lorene::Scalar::poisson_angu(), and Lorene::Tensor::triad.
◆ exponential_filter_r()
|
virtualinherited |
Applies exponential filters to all components (see Scalar::exponential_filter_r ).
Does a loop for Cartesian components, and works in terms of the rr-component,  ,
,  ,
, W, X, T for spherical components.
Reimplemented from Lorene::Tensor.
Definition at line 449 of file sym_tensor.C.
References Lorene::Tensor::cmp, Lorene::Scalar::div_r(), Lorene::Sym_tensor::eta(), Lorene::Scalar::exponential_filter_r(), Lorene::Map::get_bvect_cart(), Lorene::Map::get_bvect_spher(), Lorene::Base_vect::identify(), Lorene::Tensor::mp, Lorene::Sym_tensor::mu(), Lorene::Tensor::n_comp, Lorene::Tensor::operator()(), Lorene::Sym_tensor::set_auxiliary(), Lorene::Tensor::triad, Lorene::Sym_tensor::ttt(), Lorene::Sym_tensor::www(), and Lorene::Sym_tensor::xxx().
◆ exponential_filter_ylm()
|
virtualinherited |
Applies exponential filters to all components (see Scalar::exponential_filter_ylm ).
Does a loop for Cartesian components, and works in terms of the r-component,  ,
,  ,
, W, X, T for spherical components.
Reimplemented from Lorene::Tensor.
Definition at line 474 of file sym_tensor.C.
References Lorene::Tensor::cmp, Lorene::Scalar::div_r(), Lorene::Sym_tensor::eta(), Lorene::Scalar::exponential_filter_ylm(), Lorene::Map::get_bvect_cart(), Lorene::Map::get_bvect_spher(), Lorene::Base_vect::identify(), Lorene::Tensor::mp, Lorene::Sym_tensor::mu(), Lorene::Tensor::n_comp, Lorene::Tensor::operator()(), Lorene::Sym_tensor::set_auxiliary(), Lorene::Tensor::triad, Lorene::Sym_tensor::ttt(), Lorene::Sym_tensor::www(), and Lorene::Sym_tensor::xxx().
◆ exponential_filter_ylm_phi()
|
virtualinherited |
Applies exponential filters to all components (see Scalar::exponential_filter_ylm_phi ).
Works only for Cartesian components.
Reimplemented in Lorene::Scalar.
Definition at line 1102 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Map::get_bvect_cart(), Lorene::Base_vect::identify(), Lorene::Tensor::mp, Lorene::Tensor::n_comp, and Lorene::Tensor::triad.
◆ get_index_type() [1/2]
|
inlineinherited |
Gives the type (covariant or contravariant) of the index number i .
i must be strictly lower than valence and obey the following convention:
i= 0 : first indexi= 1 : second index- and so on...
- Returns
- COV for a covariant index, CON for a contravariant one.
Definition at line 927 of file tensor.h.
References Lorene::Tensor::type_indice.
◆ get_index_type() [2/2]
|
inlineinherited |
Returns the types of all the indices.
- Returns
- 1-D array of integers (class
Itbl) of sizevalence
containing the type of each index,COVfor a covariant one andCON
for a contravariant one.
Definition at line 937 of file tensor.h.
References Lorene::Tensor::type_indice.
◆ get_met_div()
|
inlineinherited |
Returns the metric with respect to which the divergence and the trace are defined.
Definition at line 672 of file sym_tensor.h.
References Lorene::Sym_tensor_trans::met_div.
◆ get_mp()
|
inlineinherited |
◆ get_n_comp()
|
inlineinherited |
Returns the number of stored components.
Definition at line 913 of file tensor.h.
References Lorene::Tensor::n_comp.
◆ get_place_met()
|
protectedinherited |
Returns the position of the pointer on metre in the array met_depend .
Definition at line 453 of file tensor.C.
References Lorene::Tensor::met_depend.
◆ get_tilde_B_from_TT_trace()
|
protectedinherited |
Computes 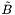 (see
(see Sym_tensor::p_tilde_b ) from its transverse-traceless part and the trace.
Definition at line 534 of file sym_tensor_aux.C.
References Lorene::Scalar::get_etat(), and Lorene::Tensor::triad.
◆ get_triad()
|
inlineinherited |
Returns the vectorial basis (triad) on which the components are defined.
Definition at line 907 of file tensor.h.
References Lorene::Tensor::triad.
◆ get_valence()
|
inlineinherited |
◆ inc_dzpuis()
|
virtualinherited |
Increases by inc units the value of dzpuis and changes accordingly the values in the compactified external domain (CED).
Reimplemented in Lorene::Scalar.
Definition at line 826 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), and Lorene::Tensor::n_comp.
◆ indices()
|
virtualinherited |
Returns the indices of a component given by its position in the array cmp .
- Parameters
-
pos [input] position in the array cmpof the pointer to theScalarrepresenting a component
- Returns
- 1-D array of integers (class
Itbl) of sizevalencegiving the value of each index for the component located at the positionposin the arraycmp, with the following storage convention:Itbl(0): value of the first index (1, 2 or 3)Itbl(1): value of the second index (1, 2 or 3)- and so on...
Reimplemented from Lorene::Tensor.
Definition at line 313 of file tensor_sym.C.
References Lorene::Tensor_sym::id_sym1, Lorene::Tensor_sym::id_sym2, Lorene::Tensor::n_comp, Lorene::Itbl::set(), and Lorene::Tensor::valence.
◆ inverse()
|
protectedinherited |
Returns a pointer on the inverse of the Sym_tensor
(seen as a matrix).
Definition at line 375 of file sym_tensor.C.
References Lorene::Tensor::mp, Lorene::Tensor::operator()(), Lorene::Tensor::set(), Lorene::Sym_tensor::Sym_tensor(), Lorene::Tensor::triad, and Lorene::Tensor::type_indice.
◆ khi()
| const Scalar & Lorene::Sym_tensor_tt::khi | ( | ) | const |
Gives the field 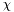 such that the component
such that the component 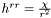 .
.
Definition at line 119 of file sym_tensor_tt_etamu.C.
References Lorene::Scalar::mult_r(), p_khi, and Lorene::Tensor::triad.
◆ longit_pot()
|
inherited |
Computes the vector potential 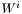 of longitudinal part of the tensor (see documentation of method
of longitudinal part of the tensor (see documentation of method transverse() above).
- Parameters
-
gam metric with respect to the transverse decomposition is performed par parameters for the vector Poisson equation method_poisson type of method for solving the vector Poisson equation to get the longitudinal part (see method Vector::poisson)
Definition at line 149 of file sym_tensor_decomp.C.
References Lorene::Tensor::dec_dzpuis(), Lorene::Tensor::derive_con(), Lorene::Tensor_sym::derive_con(), Lorene::diffrel(), Lorene::Sym_tensor::divergence(), Lorene::Tensor::divergence(), Lorene::Map::get_mg(), Lorene::Mg3d::get_nzone(), Lorene::Tensor::get_place_met(), Lorene::maxabs(), Lorene::Tensor::mp, Lorene::Sym_tensor::p_longit_pot, Lorene::Vector::poisson(), and Lorene::Tensor::set_dependance().
◆ mu()
Gives the field  (see member
(see member p_mu ).
Definition at line 154 of file sym_tensor_aux.C.
References Lorene::Scalar::div_tant(), Lorene::Scalar::dsdt(), Lorene::Scalar::get_dzpuis(), Lorene::Tensor::mp, Lorene::Scalar::mult_r_dzpuis(), Lorene::Tensor::operator()(), Lorene::Sym_tensor::p_mu, Lorene::Map::poisson_angu(), Lorene::Scalar::poisson_angu(), Lorene::Scalar::stdsdp(), and Lorene::Tensor::triad.
◆ operator()() [1/4]
Returns the value of a component (read-only version).
- Parameters
-
ind 1-D Itblof sizevalencecontaining the values of each index specifing the component, with the following storage convention:ind(0): value of the first index (1, 2 or 3)ind(1): value of the second index (1, 2 or 3)- and so on...
- Returns
- reference on the component specified by
ind
Definition at line 808 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Itbl::get_dim(), Lorene::Itbl::get_ndim(), Lorene::Tensor::position(), and Lorene::Tensor::valence.
◆ operator()() [2/4]
|
inherited |
Returns the value of a component for a tensor of valence 2 (read-only version).
- Parameters
-
i1 value of the first index (1, 2 or 3) i2 value of the second index (1, 2 or 3)
- Returns
- reference on the component specified by
(i1,i2)
Definition at line 770 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::position(), Lorene::Itbl::set(), and Lorene::Tensor::valence.
◆ operator()() [3/4]
|
inherited |
Returns the value of a component for a tensor of valence 3 (read-only version).
- Parameters
-
i1 value of the first index (1, 2 or 3) i2 value of the second index (1, 2 or 3) i3 value of the third index (1, 2 or 3)
- Returns
- reference on the component specified by
(i1,i2,i3)
Definition at line 781 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::position(), Lorene::Itbl::set(), and Lorene::Tensor::valence.
◆ operator()() [4/4]
|
inherited |
Returns the value of a component for a tensor of valence 4 (read-only version).
- Parameters
-
i1 value of the first index (1, 2 or 3) i2 value of the second index (1, 2 or 3) i3 value of the third index (1, 2 or 3) i4 value of the fourth index (1, 2 or 3)
- Returns
- reference on the component specified by
(i1,i2,i3,i4)
Definition at line 793 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::position(), Lorene::Itbl::set(), and Lorene::Tensor::valence.
◆ operator+=()
|
inherited |
+= Tensor
Definition at line 581 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), Lorene::Tensor::indices(), Lorene::Tensor::n_comp, Lorene::Tensor::position(), Lorene::Tensor::triad, Lorene::Tensor::type_indice, and Lorene::Tensor::valence.
◆ operator-=()
|
inherited |
-= Tensor
Definition at line 597 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), Lorene::Tensor::indices(), Lorene::Tensor::n_comp, Lorene::Tensor::position(), Lorene::Tensor::triad, Lorene::Tensor::type_indice, and Lorene::Tensor::valence.
◆ operator=() [1/5]
|
virtual |
Assignment to another Sym_tensor_tt.
Definition at line 144 of file sym_tensor_tt.C.
References del_deriv(), Lorene::Sym_tensor_trans::operator=(), and p_khi.
◆ operator=() [2/5]
|
virtual |
Assignment to a Sym_tensor_trans.
Reimplemented from Lorene::Sym_tensor_trans.
Definition at line 156 of file sym_tensor_tt.C.
References del_deriv(), and Lorene::Sym_tensor_trans::operator=().
◆ operator=() [3/5]
|
virtual |
Assignment to a Sym_tensor.
Reimplemented from Lorene::Sym_tensor_trans.
Definition at line 166 of file sym_tensor_tt.C.
References del_deriv(), and Lorene::Sym_tensor_trans::operator=().
◆ operator=() [4/5]
|
virtual |
Assignment to a Tensor_sym.
Reimplemented from Lorene::Sym_tensor_trans.
Definition at line 175 of file sym_tensor_tt.C.
References del_deriv(), and Lorene::Sym_tensor_trans::operator=().
◆ operator=() [5/5]
|
virtual |
Assignment to a Tensor.
Reimplemented from Lorene::Sym_tensor_trans.
Definition at line 184 of file sym_tensor_tt.C.
References del_deriv(), and Lorene::Sym_tensor_trans::operator=().
◆ poisson() [1/2]
|
inherited |
Computes the solution of a tensorial transverse Poisson equation with *this 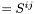 as a source:
as a source:
![\[ \Delta h^{ij} = S^{ij}. *\]](form_754.png)
In particular, it makes an iteration on the trace of the result, using Sym_tensor::set_WX_det_one.
- Parameters
-
h_guess a pointer on a guess for the trace of the result; it is passed to Sym_tensor::set_WX_det_one.
- Returns
- solution
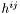 of the above equation with the boundary condition
of the above equation with the boundary condition 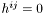 at spatial infinity.
at spatial infinity.
Definition at line 102 of file sym_tensor_trans_pde.C.
References Lorene::Map_af::get_alpha(), Lorene::Map_af::get_beta(), Lorene::Map::get_mg(), Lorene::Mg3d::get_np(), Lorene::Mg3d::get_nt(), Lorene::Mg3d::get_nzone(), Lorene::Mg3d::get_type_r(), Lorene::Sym_tensor_trans::met_div, Lorene::Tensor::mp, and Lorene::Tensor::triad.
◆ poisson() [2/2]
| Sym_tensor_tt Lorene::Sym_tensor_tt::poisson | ( | int | dzfin = 2 | ) | const |
Computes the solution of a tensorial TT Poisson equation with *this 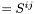 as a source:
as a source:
![\[ \Delta h^{ij} = S^{ij} *\]](form_764.png)
.
- Parameters
-
dzfin [input] the dzpuisfor all the components of the result (see the documentation forScalar).
- Returns
- solution
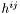 of the above equation with the boundary condition
of the above equation with the boundary condition 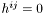 at spatial infinity.
at spatial infinity.
Definition at line 65 of file sym_ttt_poisson.C.
References Lorene::Scalar::get_etat(), Lorene::Map::get_mg(), Lorene::Mg3d::get_nzone(), Lorene::Sym_tensor_trans::met_div, Lorene::Tensor::mp, Lorene::Tensor::operator()(), and Lorene::Tensor::triad.
◆ position()
|
virtualinherited |
Returns the position in the array cmp of a component given by its indices.
- Parameters
-
ind [input] 1-D array of integers (class Itbl) of sizevalencegiving the values of each index specifing the component, with the following storage convention:ind(0): value of the first index (1, 2 or 3)ind(1): value of the second index (1, 2 or 3)- and so on...
- Returns
- position in the array
cmpof the pointer to theScalarcontaining the component specified byind
Reimplemented from Lorene::Tensor.
Definition at line 248 of file tensor_sym.C.
References Lorene::Itbl::get_dim(), Lorene::Itbl::get_ndim(), Lorene::Tensor_sym::id_sym1, Lorene::Tensor_sym::id_sym2, Lorene::Itbl::set(), and Lorene::Tensor::valence.
◆ sauve()
|
virtualinherited |
Save in a binary file.
Reimplemented from Lorene::Tensor.
Definition at line 375 of file tensor_sym.C.
References Lorene::fwrite_be(), Lorene::Tensor_sym::id_sym1, Lorene::Tensor_sym::id_sym2, and Lorene::Tensor::sauve().
◆ set() [1/4]
Returns the value of a component (read/write version).
- Parameters
-
ind 1-D Itblof sizevalencecontaining the values of each index specifing the component, with the following storage convention:ind(0): value of the first index (1, 2 or 3)ind(1): value of the second index (1, 2 or 3)- and so on...
- Returns
- modifiable reference on the component specified by
ind
Definition at line 664 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), Lorene::Itbl::get_dim(), Lorene::Itbl::get_ndim(), Lorene::Tensor::position(), and Lorene::Tensor::valence.
◆ set() [2/4]
|
inherited |
Returns the value of a component for a tensor of valence 2 (read/write version).
- Parameters
-
i1 value of the first index (1, 2 or 3) i2 value of the second index (1, 2 or 3)
- Returns
- modifiable reference on the component specified by
(i1,i2)
Definition at line 616 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), Lorene::Tensor::position(), Lorene::Itbl::set(), and Lorene::Tensor::valence.
◆ set() [3/4]
|
inherited |
Returns the value of a component for a tensor of valence 3 (read/write version).
- Parameters
-
i1 value of the first index (1, 2 or 3) i2 value of the second index (1, 2 or 3) i3 value of the third index (1, 2 or 3)
- Returns
- modifiable reference on the component specified by
(i1,i2,i3)
Definition at line 631 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), Lorene::Tensor::position(), Lorene::Itbl::set(), and Lorene::Tensor::valence.
◆ set() [4/4]
|
inherited |
Returns the value of a component for a tensor of valence 4 (read/write version).
- Parameters
-
i1 value of the first index (1, 2 or 3) i2 value of the second index (1, 2 or 3) i3 value of the third index (1, 2 or 3) i4 value of the fourth index (1, 2 or 3)
- Returns
- modifiable reference on the component specified by
(i1,i2,i3,i4)
Definition at line 647 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), Lorene::Tensor::position(), Lorene::Itbl::set(), and Lorene::Tensor::valence.
◆ set_A_tildeB()
| void Lorene::Sym_tensor_tt::set_A_tildeB | ( | const Scalar & | a_in, |
| const Scalar & | tb_in, | ||
| Param * | par_bc = 0x0, |
||
| Param * | par_mat = 0x0 |
||
| ) |
Assigns the derived members A and 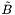 .
.
Other derived members are deduced from the divergence-and trace-free conditions.
- Parameters
-
a_in the Apotential (seeSym_tensor::p_aaa)tb_in the 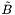 potential (see
potential (see Sym_tensor::p_tilde_b)
Definition at line 490 of file sym_tensor_tt_etamu.C.
References Lorene::Tensor::mp, and Lorene::Sym_tensor_trans::set_AtB_trace().
◆ set_AtB_trace()
|
inherited |
Assigns the derived members A , 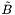 and the trace.
and the trace.
Other derived members are deduced from the divergence-free condition.
- Parameters
-
a_in the Apotential (seeSym_tensor::p_aaa)tb_in the 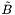 potential (see
potential (see Sym_tensor::p_tilde_b)trace the trace of the Sym_tensor.
Definition at line 305 of file sym_tensor_trans_aux.C.
References Lorene::Scalar::check_dzpuis(), Lorene::Tensor::mp, Lorene::Sym_tensor::p_aaa, Lorene::Sym_tensor::p_tilde_b, Lorene::Sym_tensor::set_auxiliary(), Lorene::Sym_tensor_trans::sol_Dirac_A(), Lorene::Sym_tensor_trans::sol_Dirac_tilde_B(), and Lorene::Tensor::triad.
◆ set_AtBtt_det_one()
|
inherited |
Assigns the derived member A and computes 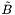 from its TT-part (see
from its TT-part (see Sym_tensor::compute_tilde_B_tt() ).
Other derived members are deduced from the divergence-free condition. Finally, it computes the trace so that *this + the flat metric has a determinant equal to 1. It then updates the components accordingly. This function makes an iteration until the relative difference in the trace between two steps is lower than precis .
- Parameters
-
a_in the Apotential (seeSym_tensor::p_aaa)tbtt_in the TT-part of 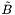 potential (see
potential (see Sym_tensor::p_tilde_bandSym_tensor::compute_tilde_B_tt())h_prev a pointer on a guess for the trace of *this; if null, then the iteration starts from 0.precis relative difference in the trace computation to end the iteration. it_max maximal number of iterations.
Definition at line 140 of file sym_tensor_trans_aux.C.
References Lorene::abs(), Lorene::Scalar::check_dzpuis(), Lorene::Scalar::get_spectral_base(), Lorene::Sym_tensor::get_tilde_B_from_TT_trace(), Lorene::Tensor::inc_dzpuis(), Lorene::max(), Lorene::Sym_tensor_trans::met_div, Lorene::Tensor::mp, Lorene::Sym_tensor::p_aaa, Lorene::Sym_tensor::p_tilde_b, Lorene::Sym_tensor_trans::p_trace, Lorene::Sym_tensor_trans::p_tt, Lorene::Sym_tensor::set_auxiliary(), Lorene::Scalar::set_etat_zero(), Lorene::Scalar::set_spectral_base(), Lorene::Sym_tensor_trans::sol_Dirac_A(), Lorene::Sym_tensor_trans::sol_Dirac_tilde_B(), and Lorene::Tensor::triad.
◆ set_auxiliary()
|
inherited |
Assigns the component 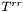 and the derived members
and the derived members p_eta , p_mu , p_www, p_xxx and p_ttt , fro, their values and 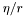 ,
, 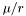 .
.
It updates the other components accordingly.
Definition at line 269 of file sym_tensor_aux.C.
References Lorene::Scalar::check_dzpuis(), Lorene::Sym_tensor::del_deriv(), Lorene::Scalar::dsdt(), Lorene::Scalar::get_dzpuis(), Lorene::Scalar::lapang(), Lorene::Scalar::mult_r_dzpuis(), Lorene::Sym_tensor::p_eta, Lorene::Sym_tensor::p_mu, Lorene::Sym_tensor::p_ttt, Lorene::Sym_tensor::p_www, Lorene::Sym_tensor::p_xxx, Lorene::Scalar::set_spectral_va(), Lorene::Scalar::stdsdp(), Lorene::Tensor::triad, and Lorene::Valeur::ylm_i().
◆ set_dependance()
|
protectedinherited |
To be used to describe the fact that the derivatives members have been calculated with met .
First it sets a null element of met_depend to &met and puts this in the list of the dependancies of met .
Definition at line 463 of file tensor.C.
References Lorene::Tensor::met_depend, and Lorene::Metric::tensor_depend.
◆ set_der_0x0()
|
protected |
Sets the pointers on derived quantities to 0x0.
Definition at line 134 of file sym_tensor_tt.C.
References p_khi.
◆ set_der_met_0x0()
|
protectedinherited |
Sets all the i-th components of met_depend specific to the class Sym_tensor (p_transverse , etc...) to 0x0.
Definition at line 338 of file sym_tensor.C.
References Lorene::Sym_tensor::p_longit_pot, and Lorene::Sym_tensor::p_transverse.
◆ set_etat_nondef()
|
virtualinherited |
Sets the logical state of all components to ETATNONDEF
(undefined state).
Reimplemented in Lorene::Scalar.
Definition at line 499 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), Lorene::Tensor::n_comp, and Lorene::Scalar::set_etat_nondef().
◆ set_etat_qcq()
|
virtualinherited |
Sets the logical state of all components to ETATQCQ
(ordinary state).
Reimplemented in Lorene::Scalar.
Definition at line 491 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), Lorene::Tensor::n_comp, and Lorene::Scalar::set_etat_qcq().
◆ set_etat_zero()
|
virtualinherited |
Sets the logical state of all components to ETATZERO
(zero state).
Reimplemented in Lorene::Scalar.
Definition at line 507 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::del_deriv(), Lorene::Tensor::n_comp, and Lorene::Scalar::set_etat_zero().
◆ set_hrr_mu_det_one()
|
inherited |
Assigns the rr component and the derived member  .
.
Other derived members are deduced from the divergence-free condition. Finally, it computes T (Sym_tensor::p_ttt ) so that *this + the flat metric has a determinant equal to 1. It then updates the components accordingly. This function makes an iteration until the relative difference in T between two steps is lower than precis .
- Parameters
-
hrr the rr component of the tensor, mu_in the  potential,
potential, precis relative difference in the trace computation to end the iteration. it_max maximal number of iterations.
Definition at line 120 of file sym_tensor_trans_aux.C.
References Lorene::Scalar::check_dzpuis(), Lorene::Tensor::dec_dzpuis(), Lorene::Tensor::inc_dzpuis(), Lorene::Sym_tensor_trans::met_div, Lorene::Tensor::mp, Lorene::Sym_tensor::p_mu, set_rr_mu(), Lorene::Sym_tensor_trans::trace_from_det_one(), and Lorene::Tensor::triad.
◆ set_index_type() [1/2]
|
inlineinherited |
Sets the type of the index number i .
i must be strictly lower than valence and obey the following convention:
i= 0 : first indexi= 1 : second index- and so on...
- Returns
- reference on the type that can be modified (
COVfor a covariant index,CONfor a contravariant one)
Definition at line 950 of file tensor.h.
References Lorene::Itbl::set(), and Lorene::Tensor::type_indice.
◆ set_index_type() [2/2]
|
inlineinherited |
Sets the types of all the indices.
- Returns
- a reference on the 1-D array of integers (class
Itbl) of sizevalencethat can be modified (COVfor a covariant one andCONfor a contravariant one)
Definition at line 959 of file tensor.h.
References Lorene::Tensor::type_indice.
◆ set_khi_eta_mu()
| void Lorene::Sym_tensor_tt::set_khi_eta_mu | ( | const Scalar & | khi_i, |
| const Scalar & | eta_i, | ||
| const Scalar & | mu_i | ||
| ) |
Sets the component 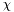 , as well as the angular potentials
, as well as the angular potentials  and
and  (see members
(see members p_khi , p_eta and p_mu ).
The components are updated consistently by a call to the method update() .
- Parameters
-
khi_i [input] value of 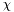
eta_i [input] angular potential 
mu_i [input] angular potential 
Definition at line 263 of file sym_tensor_tt_etamu.C.
References Lorene::Scalar::get_dzpuis(), Lorene::Sym_tensor::p_eta, p_khi, Lorene::Sym_tensor::p_mu, Lorene::Tensor::triad, and update().
◆ set_khi_mu()
| void Lorene::Sym_tensor_tt::set_khi_mu | ( | const Scalar & | khi_i, |
| const Scalar & | mu_i, | ||
| int | dzp = 0, |
||
| Param * | par1 = 0x0, |
||
| Param * | par2 = 0x0, |
||
| Param * | par3 = 0x0 |
||
| ) |
Sets the component 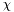 , as well as the angular potential
, as well as the angular potential  (see member
(see member p_khi and p_mu ).
The angular potential  (member
(member p_eta ) is deduced from the divergence free condition. The tensor components are updated consistently by a call to the method update() .
- Parameters
-
khi_i [input] value of 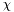
mu_i [input] angular potential 
dzp [input] dzpuisparameter of the resulting tensor components
Definition at line 291 of file sym_tensor_tt_etamu.C.
References Lorene::Scalar::check_dzpuis(), eta(), Lorene::Tensor::mp, p_khi, Lorene::Sym_tensor::p_mu, Lorene::Tensor::triad, and update().
◆ set_longit_trans()
|
inherited |
Assigns the derived members p_longit_pot and p_transverse and updates the components accordingly.
(see the documentation of these derived members for details)
Definition at line 94 of file sym_tensor_decomp.C.
References Lorene::Tensor::dec_dzpuis(), Lorene::Sym_tensor::del_deriv(), Lorene::Tensor::get_index_type(), Lorene::Sym_tensor_trans::get_met_div(), Lorene::Tensor::get_place_met(), Lorene::Vector::ope_killing(), Lorene::Sym_tensor::p_longit_pot, Lorene::Sym_tensor::p_transverse, and Lorene::Tensor::set_dependance().
◆ set_rr_eta_mu()
| void Lorene::Sym_tensor_tt::set_rr_eta_mu | ( | const Scalar & | hrr, |
| const Scalar & | eta_i, | ||
| const Scalar & | mu_i | ||
| ) |
Sets the component 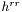 , as well as the angular potentials
, as well as the angular potentials  and
and  (see members
(see members p_eta and p_mu ).
The other components are updated consistently by a call to the method update() .
- Parameters
-
hrr [input] value of 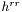
eta_i [input] angular potential 
mu_i [input] angular potential 
Definition at line 218 of file sym_tensor_tt_etamu.C.
References Lorene::Scalar::get_dzpuis(), Lorene::Sym_tensor::p_eta, Lorene::Sym_tensor::p_mu, Lorene::Tensor::triad, and update().
◆ set_rr_mu()
Sets the component 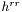 , as well as the angular potential
, as well as the angular potential  (see member
(see member p_mu ).
The angular potential  (member
(member p_eta ) is deduced from the divergence free condition. The other tensor components are updated consistently by a call to the method update() .
- Parameters
-
hrr [input] value of 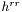
mu_i [input] angular potential 
Definition at line 241 of file sym_tensor_tt_etamu.C.
References eta(), Lorene::Scalar::get_dzpuis(), Lorene::Sym_tensor::p_mu, Lorene::Tensor::triad, and update().
◆ set_triad()
|
inherited |
Assigns a new vectorial basis (triad) of decomposition.
NB: this function modifies only the member triad and leave unchanged the components (member cmp ). In order to change them coherently with the new basis, the function change_triad(const Base_vect& ) must be called instead.
Definition at line 529 of file tensor.C.
References Lorene::Tensor::triad.
◆ set_tt_part_det_one()
|
inherited |
Assignes the TT-part of the tensor.
The trace is deduced from the divergence-free condition, through the Dirac system on 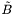 , so that
, so that *this + the flat metric has a determinant equal to 1. It then updates the components accordingly. This function makes an iteration until the relative difference in the trace between two steps is lower than precis .
- Parameters
-
hijtt the TT part for this.h_prev a pointer on a guess for the trace of *this; if null, then the iteration starts from 0.precis relative difference in the trace computation to end the iteration. it_max maximal number of iterations.
Definition at line 229 of file sym_tensor_trans_aux.C.
References Lorene::abs(), Lorene::Scalar::div_r(), eta(), Lorene::Scalar::get_spectral_base(), Lorene::Sym_tensor::get_tilde_B_from_TT_trace(), Lorene::Tensor::inc_dzpuis(), Lorene::max(), Lorene::Tensor::mp, Lorene::Sym_tensor::mu(), Lorene::Sym_tensor_trans::p_trace, Lorene::Sym_tensor_trans::p_tt, Lorene::Sym_tensor::set_auxiliary(), Lorene::Scalar::set_etat_zero(), Lorene::Scalar::set_spectral_base(), Lorene::Sym_tensor_trans::sol_Dirac_tilde_B(), Lorene::Tensor::triad, Lorene::Sym_tensor::www(), and Lorene::Sym_tensor::xxx().
◆ set_tt_trace()
|
inherited |
Assigns the derived members p_tt and p_trace and updates the components accordingly.
(see the documentation of these derived members for details)
Definition at line 238 of file sym_tensor_trans.C.
References Lorene::Scalar::check_dzpuis(), Lorene::Metric::con(), Lorene::Tensor::dec_dzpuis(), Lorene::Sym_tensor_trans::del_deriv(), Lorene::Tensor_sym::derive_con(), Lorene::Sym_tensor_trans::get_met_div(), Lorene::Sym_tensor_trans::met_div, Lorene::Tensor::mp, Lorene::Sym_tensor_trans::p_trace, Lorene::Sym_tensor_trans::p_tt, and Lorene::Scalar::poisson().
◆ sol_Dirac_A()
|
protectedinherited |
Solves a system of two coupled first-order PDEs obtained from the divergence-free condition (Dirac gauge) and the requirement that the potential A (see Sym_tensor::p_aaa ) has a given value.
The system reads:
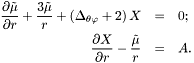
Note that this is solved only for 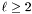 and that
and that 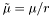 (see
(see Sym_tensor::p_mu ).
- Parameters
-
aaa [input] the source A tilde_mu [output] the solution 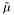
xxx [output] the solution X par_bc [input] Paramto control the boundary conditions
Definition at line 85 of file sym_tensor_trans_dirac.C.
References Lorene::Map::get_mg(), Lorene::Mg3d::get_type_r(), and Lorene::Tensor::mp.
◆ sol_Dirac_A2()
|
inherited |
Same resolution as sol_Dirac_Abound, but here the boundary conditions are the degenerate elliptic conditions encontered when solving the Kerr problem.
Definition at line 86 of file sym_tensor_trans_dirac_boundfree.C.
References Lorene::Map::get_mg(), Lorene::Mg3d::get_type_r(), and Lorene::Tensor::mp.
◆ sol_Dirac_Abound()
|
inherited |
Same resolution as sol_Dirac_A, but with inner boundary conditions added.
For now, only Robyn-type boundary conditions on 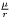 can be imposed.
can be imposed.
Definition at line 84 of file sym_tensor_trans_dirac_bound2.C.
References Lorene::Map::get_mg(), Lorene::Mg3d::get_type_r(), and Lorene::Tensor::mp.
◆ sol_Dirac_BC2()
|
inherited |
Same resolution as sol_Dirac_tilde_B, but with inner boundary conditions added.
The difference is here, one has to put B and C values in (and not only 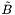 ). For now, only Robyn-type boundary conditions on
). For now, only Robyn-type boundary conditions on 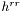 can be imposed.
can be imposed.
Definition at line 583 of file sym_tensor_trans_dirac_bound2.C.
References Lorene::Map::get_mg(), Lorene::Mg3d::get_type_r(), and Lorene::Tensor::mp.
◆ sol_Dirac_BC3()
|
inherited |
Same resolution as sol_Dirac_Abound, but here the boundary conditions are the degenerate elliptic conditions encontered when solving the Kerr problem.
Definition at line 606 of file sym_tensor_trans_dirac_boundfree.C.
References Lorene::Map::get_mg(), Lorene::Mg3d::get_type_r(), and Lorene::Tensor::mp.
◆ sol_Dirac_l01()
|
protectedinherited |
Solves the same system as Sym_tensor_trans::sol_Dirac_tilde_B but only for 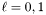 .
.
In these particular cases, W =0 the system is simpler and homogeneous solutions are different.
Definition at line 1441 of file sym_tensor_trans_dirac.C.
References Lorene::Scalar::get_etat(), and Lorene::Tensor::mp.
◆ sol_Dirac_tilde_B()
|
protectedinherited |
Solves a system of three coupled first-order PDEs obtained from divergence-free conditions (Dirac gauge) and the requirement that the potential 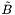 (see
(see Sym_tensor::p_tilde_b ) has a given value.
The system reads:
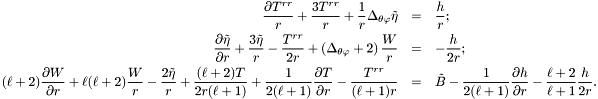
Note that 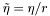 (for definitions, see derived members of
(for definitions, see derived members of Sym_tensor).
- Parameters
-
tilde_b [input] the source 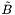
hh [input] the trace of the tensor hrr [output] the rr component of the result tilde_eta [output] the solution 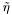
www [output] the solution W par_bc [input] Paramto control the boundary conditionspar_mat [input/output] Paramin which the operator matrix is stored.
Definition at line 586 of file sym_tensor_trans_dirac.C.
References Lorene::Map::get_mg(), Lorene::Mg3d::get_type_r(), and Lorene::Tensor::mp.
◆ spectral_display()
|
virtualinherited |
Displays the spectral coefficients and the associated basis functions of each component.
This function shows only the values greater than a given threshold.
- Parameters
-
comment comment to be printed at top of the display (default: 0x0 = nothing printed) threshold [input] Value above which a coefficient is printed (default: 1.e-7) precision [input] Number of printed digits (default: 4) ostr [input] Output stream used for the printing (default: cout)
Reimplemented in Lorene::Scalar.
Definition at line 884 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Tensor::indices(), Lorene::Tensor::n_comp, Lorene::Scalar::spectral_display(), and Lorene::Tensor::valence.
◆ std_spectral_base()
|
virtualinherited |
Sets the standard spectal bases of decomposition for each component.
To be used only with valence lower than or equal 2.
Reimplemented in Lorene::Scalar, and Lorene::Vector.
Definition at line 936 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Map::get_bvect_cart(), Lorene::Map::get_bvect_spher(), Lorene::Map::get_mg(), Lorene::Base_vect::identify(), Lorene::Tensor::indices(), Lorene::Tensor::mp, Lorene::Tensor::n_comp, Lorene::Scalar::set_spectral_base(), Lorene::Mg3d::std_base_vect_cart(), Lorene::Mg3d::std_base_vect_spher(), Lorene::Scalar::std_spectral_base(), Lorene::Tensor::triad, and Lorene::Tensor::valence.
◆ std_spectral_base_odd()
|
virtualinherited |
Sets the standard odd spectal bases of decomposition for each component.
Currently only implemented for a scalar.
Reimplemented in Lorene::Scalar.
Definition at line 992 of file tensor.C.
References Lorene::Tensor::cmp, Lorene::Scalar::std_spectral_base_odd(), and Lorene::Tensor::valence.
◆ sym_index1()
|
inlineinherited |
Number of the first symmetric index (0<= id_sym1 < valence )
Definition at line 1190 of file tensor.h.
References Lorene::Tensor_sym::id_sym1.
◆ sym_index2()
|
inlineinherited |
Number of the second symmetric index (id_sym1 < id_sym2 < valence )
Definition at line 1195 of file tensor.h.
References Lorene::Tensor_sym::id_sym2.
◆ the_trace()
|
inherited |
Returns the trace of the tensor with respect to metric *met_div.
Definition at line 273 of file sym_tensor_trans.C.
References Lorene::Sym_tensor_trans::met_div, Lorene::Sym_tensor_trans::p_trace, Lorene::Tensor::trace(), and Lorene::Tensor::type_indice.
◆ trace() [1/4]
|
inherited |
Trace on two different type indices.
- Parameters
-
ind1 first index for the contraction, with the following convention : ind1= 0 : first index of the tensorind1= 1 : second index of the tensor- and so on...
ind2 second index for the contraction
Definition at line 97 of file tensor_calculus.C.
References Lorene::Tensor::cmp, Lorene::Tensor::get_n_comp(), Lorene::Tensor::indices(), Lorene::Tensor::mp, Lorene::Tensor::position(), Lorene::Itbl::set(), Lorene::Tensor::set(), Lorene::Scalar::set_etat_zero(), Lorene::Tensor::triad, Lorene::Tensor::type_indice, and Lorene::Tensor::valence.
◆ trace() [2/4]
Trace with respect to a given metric.
- Parameters
-
ind1 first index for the contraction, with the following convention : ind1= 0 : first index of the tensorind1= 1 : second index of the tensor- and so on...
ind2 second index for the contraction gam metric used to raise or lower ind1 in order that it has a opposite type than ind2
Definition at line 156 of file tensor_calculus.C.
References Lorene::Metric::con(), Lorene::contract(), Lorene::Metric::cov(), Lorene::Tensor::trace(), Lorene::Tensor::type_indice, and Lorene::Tensor::valence.
◆ trace() [3/4]
|
inherited |
Trace on two different type indices for a valence 2 tensor.
Definition at line 183 of file tensor_calculus.C.
References Lorene::Tensor::mp, Lorene::Tensor::operator()(), Lorene::Scalar::set_etat_zero(), Lorene::Tensor::type_indice, and Lorene::Tensor::valence.
◆ trace() [4/4]
Trace with respect to a given metric for a valence 2 tensor.
- Parameters
-
gam metric used to raise or lower one of the indices, in order to take the trace
Definition at line 200 of file tensor_calculus.C.
References Lorene::Metric::con(), Lorene::contract(), Lorene::Metric::cov(), Lorene::Tensor::trace(), Lorene::Tensor::type_indice, and Lorene::Tensor::valence.
◆ trace_from_det_one()
|
inherited |
Assigns the derived member p_tt and computes the trace so that *this + the flat metric has a determinant equal to 1.
It then updates the components accordingly, with a dzpuis = 2. This function makes an iteration until the relative difference in the trace between two steps is lower than precis .
- Parameters
-
htt the transverse traceless part; all components must have dzpuis = 2. precis relative difference in the trace computation to end the iteration. it_max maximal number of iterations.
Definition at line 318 of file sym_tensor_trans.C.
References Lorene::abs(), Lorene::Scalar::check_dzpuis(), Lorene::Tensor::cmp, Lorene::Scalar::dec_dzpuis(), Lorene::Sym_tensor_trans::get_met_div(), Lorene::Tensor::get_n_comp(), Lorene::max(), Lorene::Sym_tensor_trans::met_div, Lorene::Tensor::mp, Lorene::Scalar::set_etat_zero(), and Lorene::Sym_tensor_trans::set_tt_trace().
◆ transverse()
|
inherited |
Computes the transverse part 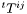 of the tensor with respect to a given metric, transverse meaning divergence-free with respect to that metric.
of the tensor with respect to a given metric, transverse meaning divergence-free with respect to that metric.
Denoting *this by 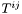 , we then have
, we then have
![\[ T^{ij} = {}^t T^{ij} + \nabla^i W^j + \nabla^j W^i \qquad\mbox{with}\quad \nabla_j {}^t T^{ij} = 0 *\]](form_719.png)
where 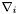 denotes the covariant derivative with respect to the given metric and
denotes the covariant derivative with respect to the given metric and 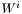 is the vector potential of the longitudinal part of
is the vector potential of the longitudinal part of 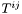 (function
(function longit_pot() below)
- Parameters
-
gam metric with respect to the transverse decomposition is performed par parameters for the vector Poisson equation method_poisson type of method for solving the vector Poisson equation to get the longitudinal part (see method Vector::poisson)
Definition at line 116 of file sym_tensor_decomp.C.
References Lorene::Tensor::cmp, Lorene::Tensor::get_place_met(), Lorene::Tensor::inc_dzpuis(), Lorene::Sym_tensor::longit_pot(), Lorene::Tensor::mp, Lorene::Tensor::n_comp, Lorene::Vector::ope_killing(), Lorene::Sym_tensor::p_transverse, Lorene::Tensor::set_dependance(), Lorene::Tensor::triad, and Lorene::Tensor::type_indice.
◆ tt_part()
|
inherited |
Returns the transverse traceless part of the tensor, the trace being defined with respect to metric *met_div.
Definition at line 287 of file sym_tensor_trans.C.
References Lorene::Metric::con(), Lorene::Tensor::dec_dzpuis(), Lorene::Scalar::derive_con(), Lorene::Tensor_sym::derive_con(), Lorene::Scalar::get_dzpuis(), Lorene::Tensor::inc_dzpuis(), Lorene::Sym_tensor_trans::met_div, Lorene::Tensor::mp, Lorene::Sym_tensor_trans::p_tt, Lorene::Scalar::poisson(), Lorene::Sym_tensor_trans::the_trace(), and Lorene::Tensor::triad.
◆ ttt()
|
inherited |
Gives the field T (see member p_ttt ).
Definition at line 193 of file sym_tensor_aux.C.
References Lorene::Sym_tensor::p_ttt, and Lorene::Tensor::triad.
◆ up()
Computes a new tensor by raising an index of *this.
- Parameters
-
ind index to be raised, with the following convention : ind1= 0 : first index of the tensorind1= 1 : second index of the tensor- and so on... (
indmust be of covariant type (COV)).
gam metric used to raise the index (contraction with the twice contravariant form of the metric on the index ind).
Definition at line 228 of file tensor_calculus.C.
References Lorene::Metric::con(), Lorene::contract(), Lorene::Tensor::indices(), Lorene::Tensor::mp, Lorene::Tensor::n_comp, Lorene::Itbl::set(), Lorene::Tensor::set(), Lorene::Tensor::triad, Lorene::Tensor::type_indice, and Lorene::Tensor::valence.
◆ up_down()
Computes a new tensor by raising or lowering all the indices of *this .
- Parameters
-
gam metric used to lower the contravariant indices and raising the covariant ones.
Definition at line 308 of file tensor_calculus.C.
References Lorene::Tensor::down(), Lorene::Tensor::Tensor(), Lorene::Tensor::type_indice, Lorene::Tensor::up(), and Lorene::Tensor::valence.
◆ update()
Computes the components 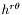 ,
, 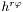 ,
, 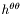 ,
, 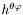 and
and 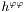 , from
, from 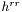 and the potentials
and the potentials  and
and  .
.
- Parameters
-
dzp dzpuisparameter of the result, i.e. of the components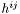 .
.
Definition at line 341 of file sym_tensor_tt_etamu.C.
References Lorene::Tensor::cmp, Lorene::Scalar::dec_dzpuis(), Lorene::Sym_tensor_trans::del_deriv(), Lorene::Scalar::div_sint(), Lorene::Scalar::dsdr(), Lorene::Scalar::dsdt(), Lorene::Tensor::mp, Lorene::Scalar::mult_cost(), Lorene::Scalar::mult_r_dzpuis(), Lorene::Scalar::mult_sint(), Lorene::Tensor::operator()(), Lorene::Sym_tensor::p_eta, Lorene::Sym_tensor::p_mu, Lorene::Map::poisson_angu(), Lorene::Scalar::poisson_angu(), Lorene::Tensor_sym::position(), Lorene::Itbl::set(), Lorene::Scalar::srdsdt(), Lorene::Scalar::srstdsdp(), Lorene::Scalar::stdsdp(), and Lorene::Tensor::triad.
◆ www()
|
inherited |
Gives the field W (see member p_www ).
Definition at line 212 of file sym_tensor_aux.C.
References Lorene::Scalar::div_tant(), Lorene::Scalar::dsdt(), Lorene::Tensor::operator()(), Lorene::Sym_tensor::p_www, Lorene::Scalar::poisson_angu(), Lorene::Scalar::stdsdp(), and Lorene::Tensor::triad.
◆ xxx()
|
inherited |
Gives the field X (see member p_xxx ).
Definition at line 243 of file sym_tensor_aux.C.
References Lorene::Scalar::div_tant(), Lorene::Scalar::dsdt(), Lorene::Tensor::operator()(), Lorene::Sym_tensor::p_xxx, Lorene::Scalar::poisson_angu(), Lorene::Scalar::stdsdp(), and Lorene::Tensor::triad.
Member Data Documentation
◆ cmp
|
protectedinherited |
◆ id_sym1
|
protectedinherited |
◆ id_sym2
|
protectedinherited |
◆ met_depend
|
mutableprotectedinherited |
◆ met_div
|
protectedinherited |
Metric with respect to which the divergence and the trace are defined.
Definition at line 617 of file sym_tensor.h.
◆ mp
|
protectedinherited |
◆ n_comp
|
protectedinherited |
◆ p_aaa
|
mutableprotectedinherited |
Field A defined from X and  insensitive to the longitudinal part of the
insensitive to the longitudinal part of the Sym_tensor (only for 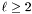 ).
).
Its definition reads
![\[ A = \frac{\partial X}{\partial r} - \frac{\mu}{r^2}. \]](form_731.png)
Definition at line 325 of file sym_tensor.h.
◆ p_derive_con
|
mutableprotectedinherited |
Array of pointers on the contravariant derivatives of this with respect to various metrics.
See the comments of met_depend . See also the comments of method derive_con() for a precise definition of a "contravariant" derivative.
◆ p_derive_cov
|
mutableprotectedinherited |
Array of pointers on the covariant derivatives of this with respect to various metrics.
See the comments of met_depend . See also the comments of method derive_cov() for the index convention of the covariant derivation.
◆ p_divergence
|
mutableprotectedinherited |
Array of pointers on the divergence of this with respect to various metrics.
See the comments of met_depend . See also the comments of method divergence() for a precise definition of a the divergence with respect to a given metric.
◆ p_eta
|
mutableprotectedinherited |
Field  such that the components
such that the components 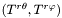 of the tensor are written (has only meaning with spherical components!):
of the tensor are written (has only meaning with spherical components!):
![\[ T^{r\theta} = {1\over r} \left( {\partial \eta \over \partial\theta} - {1\over\sin\theta} {\partial \mu \over \partial\varphi} \right) *\]](form_723.png)
![\[ T^{r\varphi} = {1\over r} \left( {1\over\sin\theta} {\partial \eta \over \partial\varphi} + {\partial \mu \over \partial\theta} \right) *\]](form_724.png)
.
Definition at line 263 of file sym_tensor.h.
◆ p_khi
|
mutableprotected |
Field 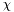 such that the component
such that the component 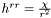 .
.
Definition at line 941 of file sym_tensor.h.
◆ p_longit_pot
|
mutableprotectedinherited |
Array of the vector potential of the longitudinal part of the tensor with respect to various metrics (see documentation of member p_transverse.
Definition at line 249 of file sym_tensor.h.
◆ p_mu
|
mutableprotectedinherited |
Field  such that the components
such that the components 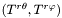 of the tensor are written (has only meaning with spherical components!):
of the tensor are written (has only meaning with spherical components!):
![\[ T^{r\theta} = {1\over r} \left( {\partial \eta \over \partial\theta} - {1\over\sin\theta} {\partial \mu \over \partial\varphi} \right) *\]](form_723.png)
![\[ T^{r\varphi} = {1\over r} \left( {1\over\sin\theta} {\partial \eta \over \partial\varphi} + {\partial \mu \over \partial\theta} \right) *\]](form_724.png)
.
Definition at line 277 of file sym_tensor.h.
◆ p_tilde_b
|
mutableprotectedinherited |
Field 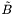 defined from
defined from 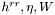 and h insensitive to the longitudinal part of the
and h insensitive to the longitudinal part of the Sym_tensor.
It is defined for each multipolar momentum 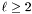 by
by
![\[ \tilde{B} = (\ell + 2) \frac{\partial W}{\partial r} + \ell(\ell + 2) \frac{W}{r} - \frac{2\eta}{r^2} + \frac{(\ell +2)T}{2r(\ell + 1)} + \frac{1}{2(\ell + 1)} \frac{\partial T}{\partial r} - \frac{h^{rr}} {(\ell + 1)r}. \]](form_734.png)
Definition at line 337 of file sym_tensor.h.
◆ p_tilde_c
|
mutableprotectedinherited |
Field 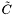 defined from
defined from 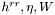 and h insensitive to the longitudinal part of the
and h insensitive to the longitudinal part of the Sym_tensor.
It is defined for each multipolar momentum 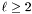 by
by
![\[ \tilde{C} = - (\ell - 1) \frac{\partial W}{\partial r} + (\ell + 1)(\ell - 1) \frac{W}{r} - \frac{2\eta}{r^2} + \frac{(\ell - 1)T}{2r\ell} - \frac{1}{2 \ell } \frac{\partial T}{\partial r} - \frac{h^{rr}} {\ell r}. \]](form_736.png)
Definition at line 349 of file sym_tensor.h.
◆ p_trace
|
mutableprotectedinherited |
Trace with respect to the metric *met_div.
Definition at line 620 of file sym_tensor.h.
◆ p_transverse
|
mutableprotectedinherited |
Array of the transverse part 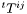 of the tensor with respect to various metrics, transverse meaning divergence-free with respect to a metric.
of the tensor with respect to various metrics, transverse meaning divergence-free with respect to a metric.
Denoting *this by 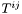 , we then have
, we then have
![\[ T^{ij} = {}^t T^{ij} + \nabla^i W^j + \nabla^j W^i \qquad\mbox{with}\quad \nabla_j {}^t T^{ij} = 0 *\]](form_719.png)
where 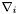 denotes the covariant derivative with respect to the given metric and
denotes the covariant derivative with respect to the given metric and 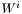 is the vector potential of the longitudinal part of
is the vector potential of the longitudinal part of 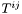 (member
(member p_longit_pot below)
Definition at line 242 of file sym_tensor.h.
◆ p_tt
|
mutableprotectedinherited |
Traceless part with respect to the metric *met_div.
Definition at line 623 of file sym_tensor.h.
◆ p_ttt
|
mutableprotectedinherited |
Field T defined as 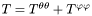 .
.
Definition at line 318 of file sym_tensor.h.
◆ p_www
|
mutableprotectedinherited |
Field W such that the components 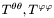 and
and 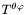 of the tensor are written (has only meaning with spherical components!):
of the tensor are written (has only meaning with spherical components!):
![\[ \frac{1}{2}\left(T^{\theta\theta} - T^{\varphi\varphi} \right) = \frac{\partial^2 W}{\partial\theta^2} - \frac{1}{\tan \theta} \frac{\partial W}{\partial \theta} - \frac{1}{\sin^2 \theta} \frac{\partial^2 W}{\partial \varphi^2} - 2\frac{\partial}{\partial \theta} \left( \frac{1}{\sin \theta} \frac{\partial X}{\partial \varphi} \right) , *\]](form_727.png)
![\[ T^{\theta\varphi} = \frac{\partial^2 X}{\partial\theta^2} - \frac{1}{\tan \theta} \frac{\partial X}{\partial \theta} - \frac{1}{\sin^2 \theta} \frac{\partial^2 X}{\partial \varphi^2} + 2\frac{\partial}{\partial \theta} \left( \frac{1}{\sin \theta} \frac{\partial W}{\partial \varphi} \right) . *\]](form_728.png)
.
Definition at line 296 of file sym_tensor.h.
◆ p_xxx
|
mutableprotectedinherited |
Field X such that the components 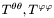 and
and 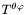 of the tensor are written (has only meaning with spherical components!):
of the tensor are written (has only meaning with spherical components!):
![\[ \frac{1}{2}\left(T^{\theta\theta} - T^{\varphi\varphi} \right) = \frac{\partial^2 W}{\partial\theta^2} - \frac{1}{\tan \theta} \frac{\partial W}{\partial \theta} - \frac{1}{\sin^2 \theta} \frac{\partial^2 W}{\partial \varphi^2} - 2\frac{\partial}{\partial \theta} \left( \frac{1}{\sin \theta} \frac{\partial X}{\partial \varphi} \right) , *\]](form_727.png)
![\[ T^{\theta\varphi} = \frac{\partial^2 X}{\partial\theta^2} - \frac{1}{\tan \theta} \frac{\partial X}{\partial \theta} - \frac{1}{\sin^2 \theta} \frac{\partial^2 X}{\partial \varphi^2} + 2\frac{\partial}{\partial \theta} \left( \frac{1}{\sin \theta} \frac{\partial W}{\partial \varphi} \right) . *\]](form_728.png)
.
Definition at line 315 of file sym_tensor.h.
◆ triad
|
protectedinherited |
◆ type_indice
|
protectedinherited |
◆ valence
|
protectedinherited |
The documentation for this class was generated from the following files:
