Bhole_binaire Class Reference
[Stars and black holes]
Binary black holes system. More...
#include <bhole.h>
Public Member Functions | |
| Bhole_binaire (Map_af &mp1, Map_af &mp2) | |
| Standard constructor. | |
| Bhole_binaire (const Bhole_binaire &) | |
| Copy. | |
| ~Bhole_binaire () | |
| Destructor. | |
| void | operator= (const Bhole_binaire &) |
| Affectation operator. | |
| Bhole & | set (int i) |
| Read/write of a component of the system. | |
| void | set_omega (double ome) |
Sets the orbital velocity to ome. | |
| void | set_pos_axe (double) |
| const Bhole & | operator() (int i) const |
| Read only of a component of the system. | |
| double | get_omega () const |
| Returns the angular velocity. | |
| void | init_bhole_binaire () |
| Initialisation of the system. | |
| double | viriel () const |
Computes the viriel error, that is the difference between the ADM and the Komar masses, calculated by the asymptotic behaviours of respectively 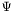 and N . and N . | |
| void | solve_lapse (double precis, double relax) |
| Solves the equation for the lapse~:
The fields are the total values excpet those with subscript | |
| void | solve_psi (double precis, double relax) |
| Solves the equation for the conformal factor~:
The fields are the total values excpet those with subscript | |
| void | solve_shift (double precis, double relax) |
| Solves the equation for the shift, using the Oohara-Nakarmure scheme~:
using the current | |
| void | fait_tkij () |
| Calculation af the extrinsic curvature tensor. | |
| void | fait_decouple () |
Calculates {tt decouple} which is used to obtain tkij_auto by the formula : tkij_auto = decouple * tkij_tot . | |
| void | set_statiques (double precis, double relax) |
Initialize the systeme to Misner Lindquist solution, that is solving for N and 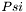 in the case in the case 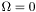 . . | |
| void | coal (double precis, double relax, int nbre_ome, double search_ome, double m1, double m2, const int sortie=0) |
| Solves the equation for a particular angular velocity, the systeme being initialized to Misner-Lindquist solution. | |
| double | adm_systeme () const |
Calculates the ADM mass of the system using : 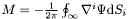 . . | |
| double | komar_systeme () const |
Calculates the Komar mass of the system using : 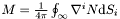 . . | |
| double | moment_systeme_inf () |
Calculates the angular momentum of the black hole using the formula at infinity : 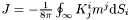 where where 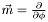 . . | |
| double | moment_systeme_hor () const |
Calculates the angular momentum of the black hole using the formula on the horizon : 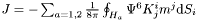 where where 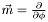 and and 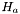 denotes the horizon of the hole a . denotes the horizon of the hole a . | |
| double | distance_propre (const int nr=65) const |
| Calculation of the proper distance between the two spheres of inversion, along the x axis. | |
| Tbl | linear_momentum_systeme_inf () const |
| void | solve_phi (double precision, double relax) |
Solve the equation for the logarithm of 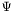 . . | |
| void | init_phi () |
Initiates the system for a resolution using the logarithm of 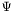 . . | |
Private Attributes | |
| Bhole | hole1 |
| Black hole one. | |
| Bhole | hole2 |
| Black hole two. | |
| Bhole * | holes [2] |
| Array on the black holes. | |
| double | pos_axe |
| double | omega |
| Position of the axis of rotation. | |
Detailed Description
Binary black holes system.
()
This class is intended for dealing with binary black holes configurations in the conformaly flat approximation.
Definition at line 752 of file bhole.h.
Constructor & Destructor Documentation
Standard constructor.
Definition at line 207 of file bhole_binaire.C.
| Bhole_binaire::Bhole_binaire | ( | const Bhole_binaire & | source | ) |
| Bhole_binaire::~Bhole_binaire | ( | ) |
Destructor.
Definition at line 222 of file bhole_binaire.C.
Member Function Documentation
| double Bhole_binaire::adm_systeme | ( | ) | const |
Calculates the ADM mass of the system using : 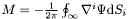 .
.
Definition at line 82 of file bhole_glob.C.
References hole1, hole2, Map_af::integrale_surface_infini(), Bhole::mp, and Bhole::psi_auto.
| void Bhole_binaire::coal | ( | double | precis, | |
| double | relax, | |||
| int | nbre_ome, | |||
| double | search_ome, | |||
| double | m1, | |||
| double | m2, | |||
| const int | sortie = 0 | |||
| ) |
Solves the equation for a particular angular velocity, the systeme being initialized to Misner-Lindquist solution.
- Parameters:
-
precis [input] : precision for the convergence (on 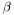 ).
). relax [input] : relaxation parameter. nbre_ome [input] : number of intermediates velocities to go from 0 to omega, typically 10.sortie [input] : flag for the output on files (0 no output files).
- Returns:
- : the virial error.
Definition at line 153 of file bhole_coal.C.
References Bhole::area(), diffrelmax(), fait_tkij(), Map::get_mg(), Mg3d::get_nzone(), Map::get_ori_x(), Bhole::get_regul(), Bhole::get_shift_auto(), hole1, hole2, Map_af::homothetie_interne(), Bhole::mp, omega, pow(), Bhole::rayon, Bhole::regul, set_omega(), solve_lapse(), solve_psi(), solve_shift(), sqrt(), Map_af::val_r(), and viriel().
| double Bhole_binaire::distance_propre | ( | const int | nr = 65 |
) | const |
Calculation of the proper distance between the two spheres of inversion, along the x axis.
- Parameters:
-
nr [input] : number of points used for the calculation.
Definition at line 258 of file bhole_glob.C.
References Map::convert_absolute(), cos(), Map::get_ori_x(), hole1, hole2, Bhole::mp, pow(), Bhole::psi_auto, and Bhole::rayon.
| void Bhole_binaire::fait_decouple | ( | ) |
Calculates {tt decouple} which is used to obtain tkij_auto by the formula : tkij_auto = decouple * tkij_tot .
(see the membre {tt Cmp decouple for more precisions about its value).
Definition at line 310 of file bhole_kij.C.
References Cmp::allocate_all(), Map::convert_absolute(), cos(), Bhole::decouple, Map::get_mg(), Mg3d::get_np(), Mg3d::get_nr(), Mg3d::get_nt(), Mg3d::get_nzone(), Map::get_ori_x(), hole1, hole2, Bhole::mp, pow(), Map::r, Cmp::set(), sin(), Cmp::std_base_scal(), Cmp::val_point(), Map::xa, Map::ya, and Map::za.
| void Bhole_binaire::fait_tkij | ( | ) |
Calculation af the extrinsic curvature tensor.
The regularisation of the shifts must have been done. All the contributions of 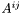 are then calculated and the total tensor must be zero on both horizons. The computation is done to avoid every singularity close to the horizons (division by N =0) for it is done in the coefficient space in the two regions surrounding the holes.
are then calculated and the total tensor must be zero on both horizons. The computation is done to avoid every singularity close to the horizons (division by N =0) for it is done in the coefficient space in the two regions surrounding the holes.
Definition at line 84 of file bhole_kij.C.
References Map::convert_absolute(), Cmp::dec2_dzpuis(), Tenseur::dec2_dzpuis(), Bhole::decouple, Bhole::fait_taij_auto(), Map_af::get_alpha(), Map_af::get_beta(), Tenseur::get_etat(), Map::get_mg(), Tenseur::get_mp(), Mg3d::get_np(), Mg3d::get_nr(), Mg3d::get_nt(), Mg3d::get_nzone(), Map::get_rot_phi(), hole1, hole2, Cmp::import_asymy(), Cmp::import_symy(), Cmp::inc2_dzpuis(), Tenseur::inc2_dzpuis(), Bhole::mp, Bhole::n_tot, Cmp::raccord(), Cmp::set(), Tenseur::set(), Tenseur::set_etat_qcq(), Tenseur::set_etat_zero(), Tenseur::set_std_base(), Bhole::taij_auto, Bhole::taij_comp, Bhole::taij_tot, Bhole::tkij_auto, Bhole::tkij_tot, Cmp::val_point(), Map::xa, Map::ya, and Map::za.
| double Bhole_binaire::get_omega | ( | ) | const [inline] |
| void Bhole_binaire::init_bhole_binaire | ( | ) |
Initialisation of the system.
Each hole is set close to a Schwarzschild one and the parts of the fields generated by the companion are calculated.
The angular velocity is set to zero.
Definition at line 235 of file bhole_binaire.C.
References fait_decouple(), Bhole::fait_n_comp(), Bhole::fait_psi_comp(), hole1, hole2, Bhole::init_bhole(), and set_omega().
| void Bhole_binaire::init_phi | ( | ) |
Initiates the system for a resolution using the logarithm of 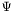 .
.
Definition at line 151 of file bhole_solve_phi.C.
References Bhole::fait_psi_comp(), hole1, hole2, Bhole::init_bhole_phi(), and set_omega().
| double Bhole_binaire::komar_systeme | ( | ) | const |
Calculates the Komar mass of the system using : 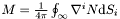 .
.
Definition at line 93 of file bhole_glob.C.
References hole1, hole2, Map_af::integrale_surface_infini(), Bhole::mp, and Bhole::n_auto.
| double Bhole_binaire::moment_systeme_hor | ( | ) | const |
Calculates the angular momentum of the black hole using the formula on the horizon : 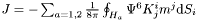 where
where 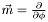 and
and 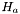 denotes the horizon of the hole a .
denotes the horizon of the hole a .
Definition at line 104 of file bhole_glob.C.
References Map::get_bvect_cart(), Map::get_bvect_spher(), Map::get_mg(), Mg3d::get_nzone(), Map::get_rot_phi(), hole1, hole2, Map_af::integrale_surface(), Bhole::mp, omega, pow(), Bhole::psi_tot, Bhole::rayon, Tenseur::set_std_base(), Cmp::std_base_scal(), Bhole::tkij_tot, Map::xa, and Map::ya.
| double Bhole_binaire::moment_systeme_inf | ( | ) |
Calculates the angular momentum of the black hole using the formula at infinity : 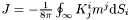 where
where 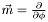 .
.
Definition at line 166 of file bhole_glob.C.
References Tenseur::annule(), Tenseur::dec2_dzpuis(), Map::get_mg(), Mg3d::get_nzone(), Map::get_ori_x(), Map::get_rot_phi(), Tenseur::gradient(), hole1, hole2, Tenseur::inc2_dzpuis(), Bhole::mp, Valeur::mult_cp(), Valeur::mult_sp(), Valeur::mult_st(), omega, Tenseur::set_std_base(), Bhole::shift_auto, and Cmp::va.
| const Bhole& Bhole_binaire::operator() | ( | int | i | ) | const [inline] |
| void Bhole_binaire::operator= | ( | const Bhole_binaire & | source | ) |
Affectation operator.
Definition at line 226 of file bhole_binaire.C.
| Bhole& Bhole_binaire::set | ( | int | i | ) | [inline] |
| void Bhole_binaire::set_omega | ( | double | ome | ) | [inline] |
| void Bhole_binaire::set_statiques | ( | double | precis, | |
| double | relax | |||
| ) |
Initialize the systeme to Misner Lindquist solution, that is solving for N and 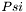 in the case
in the case 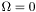 .
.
- Parameters:
-
precis [input] : precision for the convergence (on N ). relax [input] : relaxation parameter.
Definition at line 114 of file bhole_coal.C.
References diffrelmax(), Map::get_mg(), Bhole::get_n_auto(), Mg3d::get_nzone(), hole1, hole2, init_bhole_binaire(), Bhole::mp, set_omega(), solve_lapse(), and solve_psi().
| void Bhole_binaire::solve_lapse | ( | double | precis, | |
| double | relax | |||
| ) |
Solves the equation for the lapse~:
![\[ \Delta N_a = -\frac{2}{\Psi}\nabla_i \Psi_a \nabla^i N + N \Psi^4 K_{ij}K_a^{ij} \]](form_77.png)
The fields are the total values excpet those with subscript 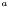 , which are the fields generated by each holes (a = 1, 2).
, which are the fields generated by each holes (a = 1, 2).
The boundary conditions are such that N =0 on both horizons. The companion contributions are then obtained.
- Parameters:
-
precis [input] : precision, for the boudary conditions are obtained by iteration. relax [input] : relaxation parameter.
Definition at line 80 of file bhole_equations_bin.C.
References Bhole::fait_n_comp(), flat_scalar_prod(), Bhole::grad_n_tot, Tenseur::gradient(), hole1, hole2, Bhole::n_auto, Bhole::n_tot, pow(), Bhole::psi_auto, Bhole::psi_tot, Cmp::raccord(), Tenseur::set(), Bhole::tkij_auto, and Bhole::tkij_tot.
| void Bhole_binaire::solve_phi | ( | double | precision, | |
| double | relax | |||
| ) |
Solve the equation for the logarithm of 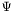 .
.
Definition at line 104 of file bhole_solve_phi.C.
References diffrelmax(), Bhole::fait_psi_comp(), flat_scalar_prod(), Mg3d::get_angu(), Map::get_mg(), Bhole::grad_psi_tot, Tenseur::gradient(), hole1, hole2, Bhole::mp, Bhole::psi_auto, Cmp::raccord(), Bhole::rayon, and Tenseur::set().
| void Bhole_binaire::solve_psi | ( | double | precis, | |
| double | relax | |||
| ) |
Solves the equation for the conformal factor~:
![\[ *\Delta \Psi_a = -\frac {\Psi^5}{8} K_{ij}K_a^{ij} \]](form_79.png)
The fields are the total values excpet those with subscript 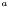 , which are the fields generated by each holes (a = 1, 2).
, which are the fields generated by each holes (a = 1, 2).
The boundary conditions are such that 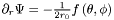 on both horizons,
on both horizons, 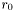 being the radii of those horizons and f the value of
being the radii of those horizons and f the value of 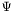 on the horizons at the preceeding step. The companion contributions are then obtained.
on the horizons at the preceeding step. The companion contributions are then obtained.
- Parameters:
-
precis [input] : precision, for the boudary conditions are being obtained by iteration. relax [input] : relaxation parameter.
Definition at line 130 of file bhole_equations_bin.C.
References Bhole::fait_psi_comp(), flat_scalar_prod(), Mg3d::get_angu(), Map::get_mg(), Mg3d::get_np(), Mg3d::get_nt(), hole1, hole2, Bhole::mp, pow(), Bhole::psi_auto, Bhole::psi_tot, Cmp::raccord(), Bhole::rayon, Tenseur::set(), Cmp::std_base_scal(), Bhole::tkij_auto, and Bhole::tkij_tot.
| void Bhole_binaire::solve_shift | ( | double | precis, | |
| double | relax | |||
| ) |
Solves the equation for the shift, using the Oohara-Nakarmure scheme~:
![\[ *\Delta \beta_a^i +\frac{1}{3} \nabla^i \left(\nabla_j \beta_a^j\right) = -6A^{ij}\frac{\nabla_i \Psi_a}{\Psi} + 2K^{ij}\nabla_j N_a \]](form_81.png)
using the current 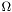 for the boudary conditions~:
for the boudary conditions~: 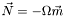 on both horizons.
on both horizons.
The fields are the total values excpet those with subscript 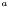 , which are the fields generated by each holes (
, which are the fields generated by each holes (a = 1, 2). The companion contributions are then obtained.
- Parameters:
-
precis [input] : precision for the solver, the boundary conditions and the inversion of the operator being obtained by iteration. relax [input] : relaxation parameter.
Definition at line 192 of file bhole_equations_bin.C.
References Cmp::filtre(), flat_scalar_prod(), Mg3d::get_angu(), Tenseur::get_etat(), Map::get_mg(), Tenseur::get_mp(), Mg3d::get_np(), Mg3d::get_nt(), Map::get_rot_phi(), Tenseur::gradient(), hole1, hole2, Bhole::mp, Bhole::n_auto, omega, Bhole::omega_local, Bhole::psi_auto, Bhole::psi_tot, Cmp::raccord(), Bhole::regul, Coord::set(), Tenseur::set(), Tenseur::set_etat_qcq(), Tenseur::set_etat_zero(), Cmp::set_etat_zero(), Tenseur::set_std_base(), Bhole::shift_auto, Mg3d::std_base_vect_cart(), Bhole::taij_tot, Bhole::tkij_tot, Map::x, Map::xa, Map::y, and Map::ya.
| double Bhole_binaire::viriel | ( | ) | const |
Computes the viriel error, that is the difference between the ADM and the Komar masses, calculated by the asymptotic behaviours of respectively 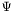 and N .
and N .
Definition at line 89 of file bhole_pseudo_viriel.C.
References Map::get_mg(), Mg3d::get_nzone(), hole1, hole2, Bhole::mp, Bhole::n_auto, and Bhole::psi_auto.
Member Data Documentation
Bhole Bhole_binaire::hole1 [private] |
Bhole Bhole_binaire::hole2 [private] |
Bhole* Bhole_binaire::holes[2] [private] |
double Bhole_binaire::omega [private] |
The documentation for this class was generated from the following files:
 1.6.1
1.6.1