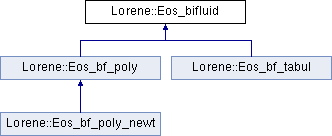
2-fluids equation of state base class. More...
#include <eos_bifluid.h>
Public Member Functions | |
| virtual | ~Eos_bifluid () |
| Destructor. More... | |
| void | operator= (const Eos_bifluid &) |
Assignment to another Eos_bifluid. More... | |
| string | get_name () const |
| Returns the EOS name. More... | |
| double | get_m1 () const |
Return the individual particule mass 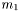 . More... . More... | |
| double | get_m2 () const |
Return the individual particule mass 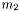 . More... . More... | |
| virtual bool | operator== (const Eos_bifluid &) const =0 |
| Comparison operator (egality) More... | |
| virtual bool | operator!= (const Eos_bifluid &) const =0 |
| Comparison operator (difference) More... | |
| virtual int | identify () const =0 |
Returns a number to identify the sub-classe of Eos_bifluid the object belongs to. More... | |
| virtual void | sauve (FILE *) const |
| Save in a file. More... | |
| virtual void | calcule_tout (const Cmp &ent1, const Cmp &ent2, const Cmp &delta2, Cmp &nbar1, Cmp &nbar2, Cmp &ener, Cmp &press, int nzet, int l_min=0) const |
General computational method for Cmp 's, it computes both baryon densities, energy and pressure profiles. More... | |
| virtual bool | nbar_ent_p (const double ent1, const double ent2, const double delta2, double &nbar1, double &nbar2) const =0 |
| Computes both baryon densities from the log-enthalpies (virtual function implemented in the derived classes). More... | |
| virtual double | nbar_ent_p1 (const double ent1) const =0 |
| Computes baryon density out of the log-enthalpy asuming that only fluid 1 is present (virtual function implemented in the derived classes). More... | |
| virtual double | nbar_ent_p2 (const double ent2) const =0 |
| Computes baryon density out of the log-enthalpy assuming that only fluid 2 is present (virtual function implemented in the derived classes). More... | |
| void | nbar_ent (const Cmp &ent1, const Cmp &ent2, const Cmp &delta2, Cmp &nbar1, Cmp &nbar2, int nzet, int l_min=0) const |
| Computes both baryon density fields from the log-enthalpy fields and the relative velocity. More... | |
| virtual double | ener_nbar_p (const double nbar1, const double nbar2, const double delta2) const =0 |
| Computes the total energy density from the baryonic densities and the relative velocity. More... | |
| Cmp | ener_ent (const Cmp &ent1, const Cmp &ent2, const Cmp &delta2, int nzet, int l_min=0) const |
| Computes the total energy density from the log-enthalpy fields and the relative velocity. More... | |
| virtual double | press_nbar_p (const double nbar1, const double nbar2, const double delta2) const =0 |
| Computes the pressure from the baryonic densities and the relative velocity. More... | |
| Cmp | press_ent (const Cmp &ent1, const Cmp &ent2, const Cmp &delta2, int nzet, int l_min=0) const |
| Computes the pressure from the log-enthalpy fields and the relative velocity. More... | |
| virtual double | get_K11 (const double n1, const double n2, const double x) const =0 |
Computes the derivative of the energy with respect to (baryonic density 1)  . More... . More... | |
| virtual double | get_K12 (const double n1, const double n2, const double x) const =0 |
Computes the derivative of the energy with respect to 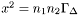 . More... . More... | |
| virtual double | get_K22 (const double n1, const double n2, const double x) const =0 |
Computes the derivative of the energy/(baryonic density 2)  . More... . More... | |
| Cmp | get_Knn (const Cmp &nbar1, const Cmp &nbar2, const Cmp &x2, int nzet, int l_min=0) const |
Computes the derivatives of the energy/(baryonic density 1)  . More... . More... | |
| Cmp | get_Kpp (const Cmp &nbar1, const Cmp &nbar2, const Cmp &x2, int nzet, int l_min=0) const |
Computes the derivatives of the energy/(baryonic density 2)  . More... . More... | |
| Cmp | get_Knp (const Cmp &nbar1, const Cmp &nbar2, const Cmp &x2, int nzet, int l_min=0) const |
Computes the derivatives of the energy with respect to 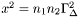 . More... . More... | |
| void | calcule (const Cmp &nbar1, const Cmp &nbar2, const Cmp &x2, int nzet, int l_min, double(Eos_bifluid::*fait)(double, double, double) const, Cmp &resu) const |
General computational method for Cmp 's ( 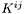 's). More... 's). More... | |
| virtual Eos * | trans2Eos () const =0 |
Makes a translation from Eos_bifluid to Eos . More... | |
Static Public Member Functions | |
| static Eos_bifluid * | eos_from_file (FILE *) |
| Construction of an EOS from a binary file. More... | |
| static Eos_bifluid * | eos_from_file (const char *fname) |
| Construction of an EOS from a formatted file. More... | |
| static Eos_bifluid * | eos_from_file (ifstream &) |
| Construction of an EOS from a formatted file. More... | |
Protected Member Functions | |
| Eos_bifluid () | |
| Standard constructor. More... | |
| Eos_bifluid (const char *name_i, double mass1, double mass2) | |
| Standard constructor with name and the two masses per particle. More... | |
| Eos_bifluid (const Eos_bifluid &) | |
| Copy constructor. More... | |
| Eos_bifluid (FILE *) | |
Constructor from a binary file (created by the function sauve(FILE*) ). More... | |
| Eos_bifluid (const char *fname) | |
| Constructor from a formatted file. More... | |
| Eos_bifluid (ifstream &fich) | |
| Construction of an EOS from a formatted file. More... | |
| virtual ostream & | operator>> (ostream &) const =0 |
| Operator >> More... | |
Protected Attributes | |
| string | name |
| EOS name. More... | |
| double | m_1 |
Individual particle mass 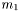 [unit:  ]. More... ]. More... | |
| double | m_2 |
Individual particle mass 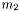 [unit:  ]. More... ]. More... | |
Friends | |
| ostream & | operator<< (ostream &, const Eos_bifluid &) |
| Display. More... | |
Detailed Description
2-fluids equation of state base class.
Fluid 1 is supposed to correspond to neutrons, whereas fluid 2 corresponds to e.g. protons. Neutron 4-velocity is 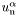 and proton one is
and proton one is 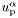
Therefore, the EOS is defined by giving two log-enthalpies AND a relative velocity as inputs. The output are then: two baryonic densities, the total energy density and pressure The enthalpies 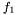 and
and 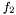 are obtained through the formula
are obtained through the formula
![\[ {\rm d}{\cal E}=f^1{\rm d}n_1+f^2{\rm d}n_2+\alpha{\rm d}\Delta^2 \label{eeosbfdefent} \]](form_263.png)
see Comer, Novak & Prix. Log-enthalpies are then defined as 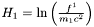 , where
, where 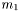 is the mass of a particle of the first fluid. (same for
is the mass of a particle of the first fluid. (same for 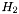 ) The relative velocity
) The relative velocity 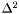 is defined as in Comer, Novak & Prix. It can be seen as the neutron velocity seen in the frame of protons (or vice-versa):
is defined as in Comer, Novak & Prix. It can be seen as the neutron velocity seen in the frame of protons (or vice-versa): 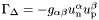 ()
()
Definition at line 180 of file eos_bifluid.h.
Constructor & Destructor Documentation
◆ Eos_bifluid() [1/6]
|
protected |
Standard constructor.
Definition at line 154 of file eos_bifluid.C.
◆ Eos_bifluid() [2/6]
|
explicitprotected |
Standard constructor with name and the two masses per particle.
Definition at line 160 of file eos_bifluid.C.
◆ Eos_bifluid() [3/6]
|
protected |
Copy constructor.
Definition at line 166 of file eos_bifluid.C.
◆ Eos_bifluid() [4/6]
|
protected |
Constructor from a binary file (created by the function sauve(FILE*) ).
This constructor is protected because any EOS construction from a binary file must be done via the function Eos_bifluid::eos_from_file(FILE*) .
Definition at line 172 of file eos_bifluid.C.
References Lorene::fread_be(), m_1, m_2, and name.
◆ Eos_bifluid() [5/6]
|
protected |
Constructor from a formatted file.
This constructor is protected because any EOS construction from a formatted file must be done via the function Eos_bifluid::eos_from_file(const char*).
The following fields have to be present in the config-file:\ name: [string] name of the EOS m_1, m_2: [double] baryon masses of the 2-fluids
Definition at line 185 of file eos_bifluid.C.
References m_1, m_2, name, and Lorene::read_variable().
◆ Eos_bifluid() [6/6]
|
protected |
Construction of an EOS from a formatted file.
This constructor is protected because any EOS construction from a formatted file must be done via the function Eos_bifluid::eos_from_file(ifstream& ).
Definition at line 211 of file eos_bifluid.C.
◆ ~Eos_bifluid()
|
virtual |
Destructor.
Definition at line 231 of file eos_bifluid.C.
Member Function Documentation
◆ calcule()
| void Lorene::Eos_bifluid::calcule | ( | const Cmp & | nbar1, |
| const Cmp & | nbar2, | ||
| const Cmp & | x2, | ||
| int | nzet, | ||
| int | l_min, | ||
| double(Eos_bifluid::*)(double, double, double) const | fait, | ||
| Cmp & | resu | ||
| ) | const |
General computational method for Cmp 's ( 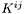 's).
's).
- Parameters
-
nbar1 [input, unit  ] baryonic density field of fluid 1 at which the derivatives are to be computed.
] baryonic density field of fluid 1 at which the derivatives are to be computed. nbar2 [input, unit  ] baryonic density field of fluid 2 at which the derivatives are to be computed
] baryonic density field of fluid 2 at which the derivatives are to be computed x2 [input, unit 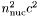 ] relative velocity
] relative velocity 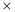 both densities at which the derivative is to be computed
both densities at which the derivative is to be computed
nzet [input] number of domains where resuis to be computed.l_min [input] index of the innermost domain is which resuis to be computed [default value: 0];resuis computed only in domains whose indices are in[l_min,l_min+nzet-1] . In the other domains, it is set to zero.fait [input] pointer on the member function of class Eos_bifluidwhich performs the pointwise calculation.resu [output] result of the computation.
Definition at line 661 of file eos_bifluid.C.
References Lorene::Cmp::get_etat().
◆ calcule_tout()
|
virtual |
General computational method for Cmp 's, it computes both baryon densities, energy and pressure profiles.
- Parameters
-
ent1 [input] the first log-enthalpy field 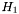 .
.
ent2 [input] the second log-enthalpy field 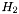 .
. delta2 [input] the relative velocity field 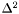
nbar1 [output] baryonic density of the first fluid nbar2 [output] baryonic density of the second fluid [unit:  ]
] ener [output] total energy density 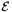 of both fluids together
of both fluids together press [output] pressure p of both fluids together nzet [input] number of domains where resuis to be computed.l_min [input] index of the innermost domain is which resuis to be computed [default value: 0];resuis computed only in domains whose indices are in[l_min,l_min+nzet-1] . In the other domains, it is set to zero.
Definition at line 286 of file eos_bifluid.C.
References Lorene::Cmp::get_etat().
◆ ener_ent()
| Cmp Lorene::Eos_bifluid::ener_ent | ( | const Cmp & | ent1, |
| const Cmp & | ent2, | ||
| const Cmp & | delta2, | ||
| int | nzet, | ||
| int | l_min = 0 |
||
| ) | const |
Computes the total energy density from the log-enthalpy fields and the relative velocity.
- Parameters
-
ent1 [input, unit:  ] log-enthalpy
] log-enthalpy 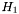
ent2 [input, unit:  ] log-enthalpy
] log-enthalpy 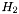
delta2 [input, unit:  ] relative velocity
] relative velocity 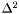
nzet number of domains where the energy density is to be computed. l_min index of the innermost domain is which the energy density is to be computed [default value: 0]; the energy density is computed only in domains whose indices are in [l_min,l_min+nzet-1] . In the other domains, it is set to zero.
- Returns
- energy density field [unit:
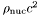 ], where
], where 
Definition at line 504 of file eos_bifluid.C.
References Lorene::Cmp::get_etat(), and Lorene::Cmp::get_mp().
◆ ener_nbar_p()
|
pure virtual |
Computes the total energy density from the baryonic densities and the relative velocity.
(virtual function implemented in the derived classes).
- Parameters
-
nbar1 [input] baryonic density of the first fluid nbar2 [input] baryonic density of the second fluid [unit:  ]
] delta2 [input, unit:  ] relative velocity
] relative velocity 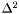
- Returns
- energy density
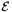 [unit:
[unit: 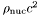 ], where
], where 
Implemented in Lorene::Eos_bf_tabul, Lorene::Eos_bf_poly_newt, and Lorene::Eos_bf_poly.
◆ eos_from_file() [1/3]
|
static |
Construction of an EOS from a binary file.
The file must have been created by the function sauve(FILE*) .
Definition at line 111 of file eos_bf_file.C.
References Lorene::fread_be().
◆ eos_from_file() [2/3]
|
static |
Construction of an EOS from a formatted file.
The following field has to be present:\ ident: [int] identifying the type of 2-fluid EOS 1 = relativistic polytropic EOS (class Eos_bf_poly ). \ 2 = Newtonian polytropic EOS (class Eos_bf_poly_newt ).
Definition at line 148 of file eos_bf_file.C.
References Lorene::read_variable().
◆ eos_from_file() [3/3]
|
static |
Construction of an EOS from a formatted file.
The fist line of the file must start by the EOS number, according to the following conventions:
- 1 = 2-fluid relativistic polytropic EOS (class
Eos_bf_poly). - 2 = 2-fluid Newtonian polytropic EOS (class
Eos_bf_poly_newt). - 3 = 2-fluid tabulated EOS (class
Eos_bf_tabul). The second line in the file should contain a name given by the user to the EOS. The following lines should contain the EOS parameters (one parameter per line), in the same order than in the class declaration.
Definition at line 190 of file eos_bf_file.C.
◆ get_K11()
|
pure virtual |
Computes the derivative of the energy with respect to (baryonic density 1)  .
.
(virtual function implemented in the derived classes).
- Parameters
-
n1 [input, unit  ] baryonic density of fluid 1 at which the derivative is to be computed
] baryonic density of fluid 1 at which the derivative is to be computed n2 [input, unit  ] baryonic density of fluid 2 at which the derivative is to be computed
] baryonic density of fluid 2 at which the derivative is to be computed x [input, unit 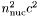 ] relative Lorentz factor
] relative Lorentz factor 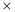 both densities at which the derivative is to be computed
both densities at which the derivative is to be computed
- Returns
- derivative
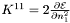
Implemented in Lorene::Eos_bf_tabul, Lorene::Eos_bf_poly_newt, and Lorene::Eos_bf_poly.
◆ get_K12()
|
pure virtual |
Computes the derivative of the energy with respect to 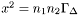 .
.
(virtual function implemented in the derived classes).
- Parameters
-
n1 [input, unit  ] baryonic density of fluid 1 at which the derivative is to be computed
] baryonic density of fluid 1 at which the derivative is to be computed n2 [input, unit  ] baryonic density of fluid 2 at which the derivative is to be computed
] baryonic density of fluid 2 at which the derivative is to be computed x [input, unit 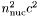 ] relative Lorentz factor
] relative Lorentz factor 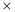 both densities at which the derivative is to be computed
both densities at which the derivative is to be computed
- Returns
- derivative
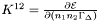
Implemented in Lorene::Eos_bf_tabul, Lorene::Eos_bf_poly_newt, and Lorene::Eos_bf_poly.
◆ get_K22()
|
pure virtual |
Computes the derivative of the energy/(baryonic density 2)  .
.
(virtual function implemented in the derived classes).
- Parameters
-
n1 [input, unit  ] baryonic density of fluid 1 at which the derivative is to be computed
] baryonic density of fluid 1 at which the derivative is to be computed n2 [input, unit  ] baryonic density of fluid 2 at which the derivative is to be computed
] baryonic density of fluid 2 at which the derivative is to be computed x [input, unit 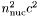 ] relative Lorentz factor
] relative Lorentz factor 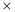 both densities at which the derivative is to be computed
both densities at which the derivative is to be computed
- Returns
- derivative
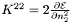
Implemented in Lorene::Eos_bf_tabul, Lorene::Eos_bf_poly_newt, and Lorene::Eos_bf_poly.
◆ get_Knn()
| Cmp Lorene::Eos_bifluid::get_Knn | ( | const Cmp & | nbar1, |
| const Cmp & | nbar2, | ||
| const Cmp & | x2, | ||
| int | nzet, | ||
| int | l_min = 0 |
||
| ) | const |
Computes the derivatives of the energy/(baryonic density 1)  .
.
- Parameters
-
nbar1 [input, unit  ] baryonic density field of fluid 1 at which the derivatives are to be computed
] baryonic density field of fluid 1 at which the derivatives are to be computed nbar2 [input, unit  ] baryonic density field of fluid 2 at which the derivatives are to be computed
] baryonic density field of fluid 2 at which the derivatives are to be computed x2 [input, unit 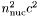 ] relative velocity
] relative velocity 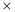 both densities at which the derivative is to be computed
both densities at which the derivative is to be computed
nzet number of domains where the derivatives are to be computed. l_min index of the innermost domain is which the derivatives are to be computed [default value: 0]; the derivatives are computed only in domains whose indices are in [l_min,l_min+nzet-1] . In the other domains, it is set to zero.
- Returns
- derivative
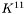 field (see
field (see get_K11)
Definition at line 750 of file eos_bifluid.C.
References calcule(), get_K11(), and Lorene::Cmp::get_mp().
◆ get_Knp()
| Cmp Lorene::Eos_bifluid::get_Knp | ( | const Cmp & | nbar1, |
| const Cmp & | nbar2, | ||
| const Cmp & | x2, | ||
| int | nzet, | ||
| int | l_min = 0 |
||
| ) | const |
Computes the derivatives of the energy with respect to 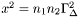 .
.
- Parameters
-
nbar1 [input, unit  ] baryonic density field of fluid 1 at which the derivatives are to be computed
] baryonic density field of fluid 1 at which the derivatives are to be computed nbar2 [input, unit  ] baryonic density field of fluid 2 at which the derivatives are to be computed
] baryonic density field of fluid 2 at which the derivatives are to be computed x2 [input, unit 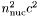 ] relative velocity
] relative velocity 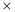 both densities at which the derivative is to be computed
both densities at which the derivative is to be computed
nzet number of domains where the derivatives are to be computed. l_min index of the innermost domain is which the derivatives are to be computed [default value: 0]; the derivatives are computed only in domains whose indices are in [l_min,l_min+nzet-1] . In the other domains, it is set to zero.
- Returns
- derivative
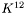 field (see
field (see get_K12)
Definition at line 761 of file eos_bifluid.C.
References calcule(), get_K12(), and Lorene::Cmp::get_mp().
◆ get_Kpp()
| Cmp Lorene::Eos_bifluid::get_Kpp | ( | const Cmp & | nbar1, |
| const Cmp & | nbar2, | ||
| const Cmp & | x2, | ||
| int | nzet, | ||
| int | l_min = 0 |
||
| ) | const |
Computes the derivatives of the energy/(baryonic density 2)  .
.
- Parameters
-
nbar1 [input, unit  ] baryonic density field of fluid 1 at which the derivatives are to be computed
] baryonic density field of fluid 1 at which the derivatives are to be computed nbar2 [input, unit  ] baryonic density field of fluid 2 at which the derivatives are to be computed
] baryonic density field of fluid 2 at which the derivatives are to be computed x2 [input, unit 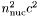 ] relative velocity
] relative velocity 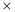 both densities at which the derivative is to be computed
both densities at which the derivative is to be computed
nzet number of domains where the derivatives are to be computed. l_min index of the innermost domain is which the derivatives are to be computed [default value: 0]; the derivatives are computed only in domains whose indices are in [l_min,l_min+nzet-1] . In the other domains, it is set to zero.
- Returns
- derivative
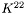 field (see
field (see get_K12)
Definition at line 772 of file eos_bifluid.C.
References calcule(), get_K22(), and Lorene::Cmp::get_mp().
◆ get_m1()
|
inline |
Return the individual particule mass 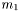 .
.
[unit:  ].
].
Definition at line 263 of file eos_bifluid.h.
References m_1.
◆ get_m2()
|
inline |
Return the individual particule mass 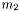 .
.
[unit:  ].
].
Definition at line 269 of file eos_bifluid.h.
References m_2.
◆ get_name()
|
inline |
◆ identify()
|
pure virtual |
Returns a number to identify the sub-classe of Eos_bifluid
the object belongs to.
Implemented in Lorene::Eos_bf_tabul, Lorene::Eos_bf_poly_newt, and Lorene::Eos_bf_poly.
◆ nbar_ent()
| void Lorene::Eos_bifluid::nbar_ent | ( | const Cmp & | ent1, |
| const Cmp & | ent2, | ||
| const Cmp & | delta2, | ||
| Cmp & | nbar1, | ||
| Cmp & | nbar2, | ||
| int | nzet, | ||
| int | l_min = 0 |
||
| ) | const |
Computes both baryon density fields from the log-enthalpy fields and the relative velocity.
- Parameters
-
ent1 [input, unit:  ] log-enthalpy
] log-enthalpy 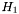
ent2 [input, unit:  ] log-enthalpy
] log-enthalpy 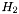
delta2 [input, unit:  ] relative velocity
] relative velocity 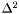
nbar1 [output] baryonic density of the first fluid nbar2 [output] baryonic density of the second fluid [unit:  ]
] nzet number of domains where the baryon density is to be computed. l_min index of the innermost domain is which the baryon density is to be computed [default value: 0]; the baryon density is computed only in domains whose indices are in [l_min,l_min+nzet-1] . In the other domains, it is set to zero.
Definition at line 416 of file eos_bifluid.C.
References Lorene::Cmp::get_etat().
◆ nbar_ent_p()
|
pure virtual |
Computes both baryon densities from the log-enthalpies (virtual function implemented in the derived classes).
- Parameters
-
ent1 [input, unit:  ] log-enthalpy
] log-enthalpy 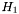
ent2 [input, unit:  ] log-enthalpy
] log-enthalpy 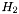
delta2 [input, unit:  ] relative velocity
] relative velocity 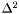
nbar1 [output] baryonic density of the first fluid nbar2 [output] baryonic density of the second fluid [unit:  ]
]
- Returns
- true if the 2-fluids model is correct, false otherwise.
Implemented in Lorene::Eos_bf_tabul, Lorene::Eos_bf_poly_newt, and Lorene::Eos_bf_poly.
◆ nbar_ent_p1()
|
pure virtual |
Computes baryon density out of the log-enthalpy asuming that only fluid 1 is present (virtual function implemented in the derived classes).
- Parameters
-
ent1 [input, unit:  ] log-enthalpy
] log-enthalpy 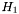
- Returns
- nbar1 baryonic density of the first fluid
Implemented in Lorene::Eos_bf_tabul, Lorene::Eos_bf_poly_newt, and Lorene::Eos_bf_poly.
◆ nbar_ent_p2()
|
pure virtual |
Computes baryon density out of the log-enthalpy assuming that only fluid 2 is present (virtual function implemented in the derived classes).
- Parameters
-
ent2 [input, unit:  ] log-enthalpy
] log-enthalpy 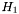
- Returns
- nbar1 baryonic density of the first fluid
Implemented in Lorene::Eos_bf_tabul, Lorene::Eos_bf_poly_newt, and Lorene::Eos_bf_poly.
◆ operator!=()
|
pure virtual |
Comparison operator (difference)
Implemented in Lorene::Eos_bf_tabul, Lorene::Eos_bf_poly_newt, and Lorene::Eos_bf_poly.
◆ operator=()
| void Lorene::Eos_bifluid::operator= | ( | const Eos_bifluid & | eosi | ) |
Assignment to another Eos_bifluid.
Definition at line 237 of file eos_bifluid.C.
◆ operator==()
|
pure virtual |
Comparison operator (egality)
Implemented in Lorene::Eos_bf_tabul, Lorene::Eos_bf_poly_newt, and Lorene::Eos_bf_poly.
◆ operator>>()
|
protectedpure virtual |
Operator >>
Implemented in Lorene::Eos_bf_tabul, Lorene::Eos_bf_poly_newt, and Lorene::Eos_bf_poly.
◆ press_ent()
| Cmp Lorene::Eos_bifluid::press_ent | ( | const Cmp & | ent1, |
| const Cmp & | ent2, | ||
| const Cmp & | delta2, | ||
| int | nzet, | ||
| int | l_min = 0 |
||
| ) | const |
Computes the pressure from the log-enthalpy fields and the relative velocity.
- Parameters
-
ent1 [input, unit:  ] log-enthalpy
] log-enthalpy 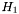
ent2 [input, unit:  ] log-enthalpy
] log-enthalpy 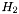
delta2 [input, unit:  ] relative velocity
] relative velocity 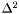
nzet number of domains where the pressure is to be computed. l_min index of the innermost domain is which the pressure is to be computed [default value: 0]; the pressure is computed only in domains whose indices are in [l_min,l_min+nzet-1] . In the other domains, it is set to zero.
- Returns
- pressure field [unit:
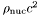 ], where
], where 
Definition at line 584 of file eos_bifluid.C.
References Lorene::Cmp::get_etat(), and Lorene::Cmp::get_mp().
◆ press_nbar_p()
|
pure virtual |
Computes the pressure from the baryonic densities and the relative velocity.
(virtual function implemented in the derived classes).
- Parameters
-
nbar1 [input] baryonic density of the first fluid nbar2 [input] baryonic density of the second fluid [unit:  ]
] delta2 [input, unit:  ] relative velocity
] relative velocity 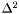
- Returns
- pressure p [unit:
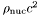 ], where
], where 
Implemented in Lorene::Eos_bf_tabul, Lorene::Eos_bf_poly_newt, and Lorene::Eos_bf_poly.
◆ sauve()
|
virtual |
Save in a file.
Reimplemented in Lorene::Eos_bf_tabul, Lorene::Eos_bf_poly_newt, and Lorene::Eos_bf_poly.
Definition at line 250 of file eos_bifluid.C.
References Lorene::fwrite_be(), identify(), m_1, m_2, and name.
◆ trans2Eos()
|
pure virtual |
Makes a translation from Eos_bifluid to Eos .
(virtual function implemented in the derived classes).
This is only useful for the construction of a Et_rot_bifluid star and ought not to be used in other situations.
- Parameters
-
relat [input] Relativistic EOS or not.
Implemented in Lorene::Eos_bf_tabul, Lorene::Eos_bf_poly_newt, and Lorene::Eos_bf_poly.
Friends And Related Function Documentation
◆ operator<<
|
friend |
Display.
Definition at line 269 of file eos_bifluid.C.
Member Data Documentation
◆ m_1
|
protected |
Individual particle mass 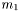
[unit:  ].
].
Definition at line 191 of file eos_bifluid.h.
◆ m_2
|
protected |
Individual particle mass 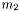
[unit:  ].
].
Definition at line 196 of file eos_bifluid.h.
◆ name
|
protected |
EOS name.
Definition at line 186 of file eos_bifluid.h.
The documentation for this class was generated from the following files:
