Class for a two-fluid (tabulated) equation of state. More...
#include <eos_bifluid.h>
Public Member Functions | |
| virtual | ~Eos_bf_tabul () |
| Destructor. More... | |
| virtual bool | operator== (const Eos_bifluid &) const |
| Comparison operator (egality) More... | |
| virtual bool | operator!= (const Eos_bifluid &) const |
| Comparison operator (difference) More... | |
| virtual int | identify () const |
Returns a number to identify the sub-classe of Eos the object belongs to. More... | |
| virtual void | sauve (FILE *) const |
| Save in a file. More... | |
| void | calcule_interpol (const Cmp &ent1, const Cmp &ent2, const Cmp &delta2, Cmp &nbar1, Cmp &nbar2, Cmp &ener, Cmp &press, Cmp &K_nn, Cmp &K_np, Cmp &K_pp, Cmp &alpha_eos, int nzet, int l_min=0) const |
General computational method for Cmp 's, it computes both baryon densities, energy and pressure profiles, the entrainment coefficient alpha and the K_{XY}'s. More... | |
| virtual bool | nbar_ent_p (const double ent1, const double ent2, const double delta2, double &nbar1, double &nbar2) const |
| Computes both baryon densities from the log-enthalpies. More... | |
| virtual double | nbar_ent_p1 (const double ent1) const |
| Computes baryon density out of the log-enthalpy asuming that only fluid 1 is present. More... | |
| virtual double | nbar_ent_p2 (const double ent2) const |
| Computes baryon density out of the log-enthalpy assuming that only fluid 2 is present. More... | |
| virtual double | ener_nbar_p (const double nbar1, const double nbar2, const double delta2) const |
| Computes the total energy density from the baryonic densities and the relative velocity. More... | |
| virtual double | press_nbar_p (const double nbar1, const double nbar2, const double delta2) const |
| Computes the pressure from the baryonic densities and the relative velocity. More... | |
| virtual double | get_K11 (const double delta2, const double ent1, const double ent2) const |
Computes the derivative of the energy with respect to (baryonic density 1)  . More... . More... | |
| virtual double | get_K12 (const double delta2, const double ent1, const double ent2) const |
Computes the derivative of the energy with respect to 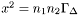 . More... . More... | |
| virtual double | get_K22 (const double delta2, const double ent1, const double ent2) const |
Computes the derivative of the energy/(baryonic density 2)  . More... . More... | |
| virtual double | ener_ent_p (const double ent1, const double ent2, const double delta_car) const |
| Computes the total energy density from the baryonic log-enthalpies and the relative velocity. More... | |
| virtual double | press_ent_p (const double ent1, const double ent2, const double delta_car) const |
| Computes the pressure from the baryonic log-enthalpies and the relative velocity. More... | |
| virtual double | alpha_ent_p (const double ent1, const double ent2, const double delta_car) const |
Computes alpha, the derivative of the total energy density with respect to 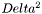 from the baryonic log-enthalpies and the relative velocity. More... from the baryonic log-enthalpies and the relative velocity. More... | |
| void | interpol_3d_bifluid (const double delta2, const double mu1, const double mu2, double &press, double &nbar1, double &nbar2, double &alpha) const |
| General method computing the pressure, both baryon densities and alpha from the values of both chemical potentials and the relative speed at the point under consideration. More... | |
| void | interpol_2d_Tbl3d (const int i, const int j, const int k, const Tbl &ytab, const Tbl &ztab, const Tbl &ftab, const Tbl &dfdytab, const Tbl &dfdztab, const Tbl &d2fdydztab, const double y, const double z, double &f, double &dfdy, double &dfdz) const |
Routine used by interpol_3d_bifluid to perform the 2D interpolation on the chemical potentials on each slice of constant 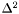 . More... . More... | |
| virtual Eos * | trans2Eos () const |
Makes a translation from Eos_bifluid to Eos . More... | |
| virtual double | csound_square_ent_p (double, const Param *) const |
Computes the sound speed squared 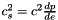 from the enthapy with extra parameters (virtual function implemented in the derived classes). More... from the enthapy with extra parameters (virtual function implemented in the derived classes). More... | |
| string | get_name () const |
| Returns the EOS name. More... | |
| double | get_m1 () const |
Return the individual particule mass 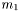 . More... . More... | |
| double | get_m2 () const |
Return the individual particule mass 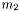 . More... . More... | |
| virtual void | calcule_tout (const Cmp &ent1, const Cmp &ent2, const Cmp &delta2, Cmp &nbar1, Cmp &nbar2, Cmp &ener, Cmp &press, int nzet, int l_min=0) const |
General computational method for Cmp 's, it computes both baryon densities, energy and pressure profiles. More... | |
| void | nbar_ent (const Cmp &ent1, const Cmp &ent2, const Cmp &delta2, Cmp &nbar1, Cmp &nbar2, int nzet, int l_min=0) const |
| Computes both baryon density fields from the log-enthalpy fields and the relative velocity. More... | |
| Cmp | ener_ent (const Cmp &ent1, const Cmp &ent2, const Cmp &delta2, int nzet, int l_min=0) const |
| Computes the total energy density from the log-enthalpy fields and the relative velocity. More... | |
| Cmp | press_ent (const Cmp &ent1, const Cmp &ent2, const Cmp &delta2, int nzet, int l_min=0) const |
| Computes the pressure from the log-enthalpy fields and the relative velocity. More... | |
| Cmp | get_Knn (const Cmp &nbar1, const Cmp &nbar2, const Cmp &x2, int nzet, int l_min=0) const |
Computes the derivatives of the energy/(baryonic density 1)  . More... . More... | |
| Cmp | get_Kpp (const Cmp &nbar1, const Cmp &nbar2, const Cmp &x2, int nzet, int l_min=0) const |
Computes the derivatives of the energy/(baryonic density 2)  . More... . More... | |
| Cmp | get_Knp (const Cmp &nbar1, const Cmp &nbar2, const Cmp &x2, int nzet, int l_min=0) const |
Computes the derivatives of the energy with respect to 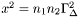 . More... . More... | |
| void | calcule (const Cmp &nbar1, const Cmp &nbar2, const Cmp &x2, int nzet, int l_min, double(Eos_bifluid::*fait)(double, double, double) const, Cmp &resu) const |
General computational method for Cmp 's ( 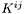 's). More... 's). More... | |
Static Public Member Functions | |
| static Eos_bifluid * | eos_from_file (FILE *) |
| Construction of an EOS from a binary file. More... | |
| static Eos_bifluid * | eos_from_file (const char *fname) |
| Construction of an EOS from a formatted file. More... | |
| static Eos_bifluid * | eos_from_file (ifstream &) |
| Construction of an EOS from a formatted file. More... | |
Protected Member Functions | |
| Eos_bf_tabul (const char *name_i, const char *table, const char *path, double mass1, double mass2) | |
| Standard constructor. More... | |
| Eos_bf_tabul (const char *name_i, const char *file_name, double mass1, double mass2) | |
| Standard constructor from the full filename. More... | |
| Eos_bf_tabul (FILE *) | |
Constructor from a binary file (created by the function sauve(FILE*) ). More... | |
| Eos_bf_tabul (ifstream &ist, const char *table) | |
| Constructor from a formatted file. More... | |
| Eos_bf_tabul (ifstream &ist) | |
| Constructor from a formatted file. More... | |
| void | read_table () |
Reads the file containing the table and initializes the arrays mu1_tab, mu2_tab, delta_car_tab, press_tab, n1_tab, n2_tab, c\ d2psdmu1dmu2_tab , c\ dpsddelta_car_tab, c\ dn1sddelta_car_tab, c\ dn2sddelta_car_tab. More... | |
| virtual ostream & | operator>> (ostream &) const |
| Operator >> More... | |
Protected Attributes | |
| string | tablename |
| Name of the file containing the tabulated data (be careful, Eos_bifluid uses char*) More... | |
| string | authors |
| Authors. More... | |
| double | delta_car_min |
| Lower boundary of the relative velocity interval. More... | |
| double | delta_car_max |
| Upper boundary of the relative velocity interval. More... | |
| double | mu1_min |
| Lower boundary of the chemical-potential interval (fluid 1 = n) More... | |
| double | mu1_max |
| Upper boundary of the chemical-potential interval (fluid 1 = n) More... | |
| double | mu2_min |
| Lower boundary of the chemical-potential interval (fluid 2 = p) More... | |
| double | mu2_max |
| Upper boundary of the chemical-potential interval (fluid 2 = p) More... | |
| Tbl * | mu1_tab |
Table of 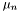 where where 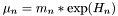 . More... . More... | |
| Tbl * | mu2_tab |
Table of 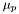 where where 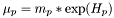 . More... . More... | |
| Tbl * | delta_car_tab |
Table of 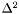 . More... . More... | |
| Tbl * | press_tab |
Table of 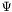 . More... . More... | |
| Tbl * | n1_tab |
Table of 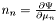 . More... . More... | |
| Tbl * | n2_tab |
Table of 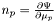 . More... . More... | |
| Tbl * | d2psdmu1dmu2_tab |
Table of 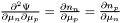 . More... . More... | |
| Tbl * | dpsddelta_car_tab |
Table of 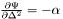 . More... . More... | |
| Tbl * | dn1sddelta_car_tab |
Table of 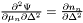 . More... . More... | |
| Tbl * | dn2sddelta_car_tab |
Table of 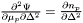 . More... . More... | |
| Tbl * | delta_car_n0 |
| Tbl * | mu1_n0 |
| Tbl * | mu2_n0 |
| Tbl * | delta_car_p0 |
| Tbl * | mu1_p0 |
| Tbl * | mu2_p0 |
| Tbl * | mu1_N |
| Tbl * | n_n_N |
| Tbl * | press_N |
| Tbl * | mu2_P |
| Tbl * | n_p_P |
| Tbl * | press_P |
| string | name |
| EOS name. More... | |
| double | m_1 |
Individual particle mass 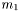 [unit:  ]. More... ]. More... | |
| double | m_2 |
Individual particle mass 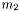 [unit:  ]. More... ]. More... | |
Private Member Functions | |
| Eos_bf_tabul (const Eos_bf_tabul &) | |
| Copy constructor. More... | |
| void | operator= (const Eos_bf_tabul &) |
Assignment to another Eos_bf_tabul. More... | |
Friends | |
| Eos_bifluid * | Eos_bifluid::eos_from_file (FILE *) |
| The construction functions from a file. More... | |
| Eos_bifluid * | Eos_bifluid::eos_from_file (ifstream &) |
Detailed Description
Class for a two-fluid (tabulated) equation of state.
This EOS depends on three variables 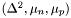 : relative velocity between the two fluids and the two enthalpies (for neutrons and protons).
: relative velocity between the two fluids and the two enthalpies (for neutrons and protons).
The interpolation through the tables is a cubic Hermite interpolation in 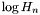 and
and 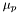 which is thermodynamically consistent, i.e. preserves the Gibbs-Duhem relation. It is defined in [Nozawa, Stergioulas, Gourgoulhon & Eriguchi, Astron. Astrophys. Suppl. Ser. 132 , 431 (1998)], and derives from a general technique presented in [Swesty, J. Comp. Phys. 127 , 118 (1996)]. A simple linear interpolation is used on
which is thermodynamically consistent, i.e. preserves the Gibbs-Duhem relation. It is defined in [Nozawa, Stergioulas, Gourgoulhon & Eriguchi, Astron. Astrophys. Suppl. Ser. 132 , 431 (1998)], and derives from a general technique presented in [Swesty, J. Comp. Phys. 127 , 118 (1996)]. A simple linear interpolation is used on 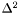 .
.
Definition at line 1436 of file eos_bifluid.h.
Constructor & Destructor Documentation
◆ Eos_bf_tabul() [1/6]
|
protected |
Standard constructor.
- Parameters
-
name_i Name of the equation of state table Name of the file containing the EOS table path Path to the directory containing the EOS file mass1 Mass of particles in fluid 1 (neutrons) mass2 Mass of particles in fluid 2 (protons)
Definition at line 84 of file eos_bf_tabul.C.
References read_table(), and tablename.
◆ Eos_bf_tabul() [2/6]
|
protected |
Standard constructor from the full filename.
- Parameters
-
name_i Name of the equation of state file_name Full name of the file containing the EOS table (including the absolute path). mass1 Mass of particles in fluid 1 (neutrons) mass2 Mass of particles in fluid 2 (protons)
Definition at line 97 of file eos_bf_tabul.C.
References read_table(), and tablename.
◆ Eos_bf_tabul() [3/6]
|
private |
Copy constructor.
◆ Eos_bf_tabul() [4/6]
|
protected |
Constructor from a binary file (created by the function sauve(FILE*) ).
This constructor is protected because any EOS construction from a binary file must be done via the function Eos_bifluid::eos_from_file(FILE*) .
Definition at line 108 of file eos_bf_tabul.C.
References read_table(), and tablename.
◆ Eos_bf_tabul() [5/6]
|
protected |
Constructor from a formatted file.
This constructor is protected because any EOS construction from a formatted file must be done via the function Eos_bifluid::eos_from_file(ifstream& ) .
- Parameters
-
ist input file stream containing a name as first line and the path to the directory containing the EOS file as second line table Name of the file containing the EOS table
Definition at line 120 of file eos_bf_tabul.C.
References read_table(), and tablename.
◆ Eos_bf_tabul() [6/6]
|
protected |
Constructor from a formatted file.
This constructor is protected because any EOS construction from a formatted file must be done via the function Eos::eos_from_file(ifstream& ) .
- Parameters
-
ist input file stream containing a name as first line and the full filename (including the path) containing the EOS file as second line
Definition at line 130 of file eos_bf_tabul.C.
References Lorene::Eos_bifluid::name, read_table(), and tablename.
◆ ~Eos_bf_tabul()
|
virtual |
Destructor.
Definition at line 146 of file eos_bf_tabul.C.
References d2psdmu1dmu2_tab, delta_car_tab, dn1sddelta_car_tab, dn2sddelta_car_tab, dpsddelta_car_tab, mu1_tab, mu2_tab, n1_tab, n2_tab, and press_tab.
Member Function Documentation
◆ alpha_ent_p()
|
virtual |
Computes alpha, the derivative of the total energy density with respect to 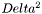 from the baryonic log-enthalpies and the relative velocity.
from the baryonic log-enthalpies and the relative velocity.
- Parameters
-
ent1 [input, unit:  ] log-enthalpy
] log-enthalpy 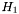 of fluid 1
of fluid 1 ent2 [input, unit:  ] log-enthalpy
] log-enthalpy 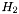 of fluid 2
of fluid 2 delta2 [input, unit:  ] relative velocity
] relative velocity 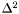
- Returns
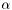
Definition at line 1177 of file eos_bf_tabul.C.
References delta_car_max, delta_car_min, Lorene::exp(), interpol_3d_bifluid(), Lorene::Eos_bifluid::m_1, Lorene::Eos_bifluid::m_2, mu1_max, and mu2_max.
◆ calcule()
|
inherited |
General computational method for Cmp 's ( 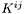 's).
's).
- Parameters
-
nbar1 [input, unit  ] baryonic density field of fluid 1 at which the derivatives are to be computed.
] baryonic density field of fluid 1 at which the derivatives are to be computed. nbar2 [input, unit  ] baryonic density field of fluid 2 at which the derivatives are to be computed
] baryonic density field of fluid 2 at which the derivatives are to be computed x2 [input, unit 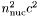 ] relative velocity
] relative velocity 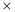 both densities at which the derivative is to be computed
both densities at which the derivative is to be computed
nzet [input] number of domains where resuis to be computed.l_min [input] index of the innermost domain is which resuis to be computed [default value: 0];resuis computed only in domains whose indices are in[l_min,l_min+nzet-1] . In the other domains, it is set to zero.fait [input] pointer on the member function of class Eos_bifluidwhich performs the pointwise calculation.resu [output] result of the computation.
Definition at line 661 of file eos_bifluid.C.
References Lorene::Cmp::get_etat().
◆ calcule_interpol()
| void Lorene::Eos_bf_tabul::calcule_interpol | ( | const Cmp & | ent1, |
| const Cmp & | ent2, | ||
| const Cmp & | delta2, | ||
| Cmp & | nbar1, | ||
| Cmp & | nbar2, | ||
| Cmp & | ener, | ||
| Cmp & | press, | ||
| Cmp & | K_nn, | ||
| Cmp & | K_np, | ||
| Cmp & | K_pp, | ||
| Cmp & | alpha_eos, | ||
| int | nzet, | ||
| int | l_min = 0 |
||
| ) | const |
General computational method for Cmp 's, it computes both baryon densities, energy and pressure profiles, the entrainment coefficient alpha and the K_{XY}'s.
- Parameters
-
ent1 [input] the first log-enthalpy field 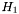 .
.
ent2 [input] the second log-enthalpy field 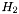 .
. delta2 [input] the relative velocity field 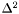
nbar1 [output] baryonic density of the first fluid nbar2 [output] baryonic density of the second fluid [unit:  ]
] ener [output] total energy density 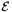 of both fluids together
of both fluids together press [output] pressure p of both fluids together K_nn [output] coefficient 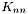
K_np [output] coefficient 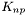
K_pp [output] coefficient 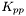
alpha_eos [output] coefficient 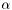
nzet [input] number of domains where resuis to be computed.l_min [input] index of the innermost domain is which resuis to be computed [default value: 0];resuis computed only in domains whose indices are in[l_min,l_min+nzet-1] . In the other domains, it is set to zero.
Definition at line 757 of file eos_bf_tabul.C.
References Lorene::Cmp::get_etat().
◆ calcule_tout()
|
virtualinherited |
General computational method for Cmp 's, it computes both baryon densities, energy and pressure profiles.
- Parameters
-
ent1 [input] the first log-enthalpy field 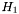 .
.
ent2 [input] the second log-enthalpy field 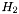 .
. delta2 [input] the relative velocity field 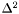
nbar1 [output] baryonic density of the first fluid nbar2 [output] baryonic density of the second fluid [unit:  ]
] ener [output] total energy density 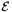 of both fluids together
of both fluids together press [output] pressure p of both fluids together nzet [input] number of domains where resuis to be computed.l_min [input] index of the innermost domain is which resuis to be computed [default value: 0];resuis computed only in domains whose indices are in[l_min,l_min+nzet-1] . In the other domains, it is set to zero.
Definition at line 286 of file eos_bifluid.C.
References Lorene::Cmp::get_etat().
◆ csound_square_ent_p()
|
inlinevirtual |
Computes the sound speed squared 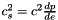 from the enthapy with extra parameters (virtual function implemented in the derived classes).
from the enthapy with extra parameters (virtual function implemented in the derived classes).
- Parameters
-
ent [input, unit: c^2] enthalpy par possible extra parameters of the EOS
- Returns
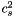 [unit: c^2]
[unit: c^2]
Definition at line 1847 of file eos_bifluid.h.
References Lorene::c_est_pas_fait().
◆ ener_ent()
|
inherited |
Computes the total energy density from the log-enthalpy fields and the relative velocity.
- Parameters
-
ent1 [input, unit:  ] log-enthalpy
] log-enthalpy 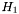
ent2 [input, unit:  ] log-enthalpy
] log-enthalpy 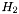
delta2 [input, unit:  ] relative velocity
] relative velocity 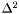
nzet number of domains where the energy density is to be computed. l_min index of the innermost domain is which the energy density is to be computed [default value: 0]; the energy density is computed only in domains whose indices are in [l_min,l_min+nzet-1] . In the other domains, it is set to zero.
- Returns
- energy density field [unit:
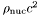 ], where
], where 
Definition at line 504 of file eos_bifluid.C.
References Lorene::Cmp::get_etat(), and Lorene::Cmp::get_mp().
◆ ener_ent_p()
|
virtual |
Computes the total energy density from the baryonic log-enthalpies and the relative velocity.
- Parameters
-
ent1 [input, unit:  ] log-enthalpy
] log-enthalpy 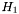 of fluid 1
of fluid 1 ent2 [input, unit:  ] log-enthalpy
] log-enthalpy 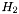 of fluid 2
of fluid 2 delta2 [input, unit:  ] relative velocity
] relative velocity 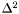
- Returns
- energy density e [unit:
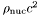 ], where
], where 
Definition at line 1142 of file eos_bf_tabul.C.
References Lorene::exp(), interpol_3d_bifluid(), Lorene::Eos_bifluid::m_1, and Lorene::Eos_bifluid::m_2.
◆ ener_nbar_p()
|
virtual |
Computes the total energy density from the baryonic densities and the relative velocity.
- Parameters
-
nbar1 [input] baryonic density of the first fluid nbar2 [input] baryonic density of the second fluid [unit:  ]
] delta2 [input, unit:  ] relative velocity
] relative velocity 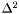
- Returns
- energy density
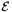 [unit:
[unit: 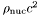 ], where
], where 
Implements Lorene::Eos_bifluid.
Definition at line 1060 of file eos_bf_tabul.C.
References Lorene::c_est_pas_fait().
◆ eos_from_file() [1/3]
|
staticinherited |
Construction of an EOS from a binary file.
The file must have been created by the function sauve(FILE*) .
Definition at line 111 of file eos_bf_file.C.
References Lorene::fread_be().
◆ eos_from_file() [2/3]
|
staticinherited |
Construction of an EOS from a formatted file.
The following field has to be present:\ ident: [int] identifying the type of 2-fluid EOS 1 = relativistic polytropic EOS (class Eos_bf_poly ). \ 2 = Newtonian polytropic EOS (class Eos_bf_poly_newt ).
Definition at line 148 of file eos_bf_file.C.
References Lorene::read_variable().
◆ eos_from_file() [3/3]
|
staticinherited |
Construction of an EOS from a formatted file.
The fist line of the file must start by the EOS number, according to the following conventions:
- 1 = 2-fluid relativistic polytropic EOS (class
Eos_bf_poly). - 2 = 2-fluid Newtonian polytropic EOS (class
Eos_bf_poly_newt). - 3 = 2-fluid tabulated EOS (class
Eos_bf_tabul). The second line in the file should contain a name given by the user to the EOS. The following lines should contain the EOS parameters (one parameter per line), in the same order than in the class declaration.
Definition at line 190 of file eos_bf_file.C.
◆ get_K11()
|
virtual |
Computes the derivative of the energy with respect to (baryonic density 1)  .
.
- Parameters
-
ent1 [input, unit:  ] log-enthalpy
] log-enthalpy 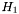 of fluid 1 at
of fluid 1 at
which the derivative is to be computedent2 [input, unit:  ] log-enthalpy
] log-enthalpy 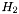 of fluid 2 at
of fluid 2 at
which the derivative is to be computeddelta2 [input, unit:  ] relative velocity
] relative velocity 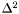 at
at
which the derivative is to be computed
- Returns
- derivative
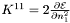
Implements Lorene::Eos_bifluid.
Definition at line 1223 of file eos_bf_tabul.C.
References alpha_ent_p(), Lorene::exp(), Lorene::Eos_bifluid::m_1, and nbar_ent_p().
◆ get_K12()
|
virtual |
Computes the derivative of the energy with respect to 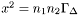 .
.
- Parameters
-
ent1 [input, unit:  ] log-enthalpy
] log-enthalpy 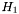 of fluid 1 at
of fluid 1 at
which the derivative is to be computedent2 [input, unit:  ] log-enthalpy
] log-enthalpy 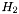 of fluid 2 at
of fluid 2 at
which the derivative is to be computeddelta2 [input, unit:  ] relative velocity
] relative velocity 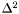 at
at
which the derivative is to be computed
- Returns
- derivative
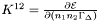
Implements Lorene::Eos_bifluid.
Definition at line 1270 of file eos_bf_tabul.C.
References alpha_ent_p(), Lorene::exp(), nbar_ent_p(), and Lorene::pow().
◆ get_K22()
|
virtual |
Computes the derivative of the energy/(baryonic density 2)  .
.
- Parameters
-
ent1 [input, unit:  ] log-enthalpy
] log-enthalpy 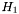 of fluid 1 at
of fluid 1 at
which the derivative is to be computedent2 [input, unit:  ] log-enthalpy
] log-enthalpy 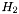 of fluid 2 at
of fluid 2 at
which the derivative is to be computeddelta2 [input, unit:  ] relative velocity
] relative velocity 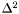 at which the derivative is to be computed
at which the derivative is to be computed
- Returns
- derivative
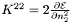
Implements Lorene::Eos_bifluid.
Definition at line 1247 of file eos_bf_tabul.C.
References alpha_ent_p(), Lorene::exp(), Lorene::Eos_bifluid::m_2, and nbar_ent_p().
◆ get_Knn()
|
inherited |
Computes the derivatives of the energy/(baryonic density 1)  .
.
- Parameters
-
nbar1 [input, unit  ] baryonic density field of fluid 1 at which the derivatives are to be computed
] baryonic density field of fluid 1 at which the derivatives are to be computed nbar2 [input, unit  ] baryonic density field of fluid 2 at which the derivatives are to be computed
] baryonic density field of fluid 2 at which the derivatives are to be computed x2 [input, unit 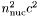 ] relative velocity
] relative velocity 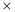 both densities at which the derivative is to be computed
both densities at which the derivative is to be computed
nzet number of domains where the derivatives are to be computed. l_min index of the innermost domain is which the derivatives are to be computed [default value: 0]; the derivatives are computed only in domains whose indices are in [l_min,l_min+nzet-1] . In the other domains, it is set to zero.
- Returns
- derivative
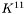 field (see
field (see get_K11)
Definition at line 750 of file eos_bifluid.C.
References Lorene::Eos_bifluid::calcule(), Lorene::Eos_bifluid::get_K11(), and Lorene::Cmp::get_mp().
◆ get_Knp()
|
inherited |
Computes the derivatives of the energy with respect to 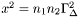 .
.
- Parameters
-
nbar1 [input, unit  ] baryonic density field of fluid 1 at which the derivatives are to be computed
] baryonic density field of fluid 1 at which the derivatives are to be computed nbar2 [input, unit  ] baryonic density field of fluid 2 at which the derivatives are to be computed
] baryonic density field of fluid 2 at which the derivatives are to be computed x2 [input, unit 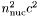 ] relative velocity
] relative velocity 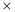 both densities at which the derivative is to be computed
both densities at which the derivative is to be computed
nzet number of domains where the derivatives are to be computed. l_min index of the innermost domain is which the derivatives are to be computed [default value: 0]; the derivatives are computed only in domains whose indices are in [l_min,l_min+nzet-1] . In the other domains, it is set to zero.
- Returns
- derivative
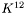 field (see
field (see get_K12)
Definition at line 761 of file eos_bifluid.C.
References Lorene::Eos_bifluid::calcule(), Lorene::Eos_bifluid::get_K12(), and Lorene::Cmp::get_mp().
◆ get_Kpp()
|
inherited |
Computes the derivatives of the energy/(baryonic density 2)  .
.
- Parameters
-
nbar1 [input, unit  ] baryonic density field of fluid 1 at which the derivatives are to be computed
] baryonic density field of fluid 1 at which the derivatives are to be computed nbar2 [input, unit  ] baryonic density field of fluid 2 at which the derivatives are to be computed
] baryonic density field of fluid 2 at which the derivatives are to be computed x2 [input, unit 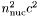 ] relative velocity
] relative velocity 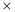 both densities at which the derivative is to be computed
both densities at which the derivative is to be computed
nzet number of domains where the derivatives are to be computed. l_min index of the innermost domain is which the derivatives are to be computed [default value: 0]; the derivatives are computed only in domains whose indices are in [l_min,l_min+nzet-1] . In the other domains, it is set to zero.
- Returns
- derivative
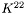 field (see
field (see get_K12)
Definition at line 772 of file eos_bifluid.C.
References Lorene::Eos_bifluid::calcule(), Lorene::Eos_bifluid::get_K22(), and Lorene::Cmp::get_mp().
◆ get_m1()
|
inlineinherited |
Return the individual particule mass 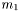 .
.
[unit:  ].
].
Definition at line 263 of file eos_bifluid.h.
References Lorene::Eos_bifluid::m_1.
◆ get_m2()
|
inlineinherited |
Return the individual particule mass 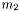 .
.
[unit:  ].
].
Definition at line 269 of file eos_bifluid.h.
References Lorene::Eos_bifluid::m_2.
◆ get_name()
|
inlineinherited |
Returns the EOS name.
Definition at line 253 of file eos_bifluid.h.
References Lorene::Eos_bifluid::name.
◆ identify()
|
virtual |
Returns a number to identify the sub-classe of Eos the object belongs to.
Implements Lorene::Eos_bifluid.
Definition at line 105 of file eos_bf_file.C.
◆ interpol_2d_Tbl3d()
| void Lorene::Eos_bf_tabul::interpol_2d_Tbl3d | ( | const int | i, |
| const int | j, | ||
| const int | k, | ||
| const Tbl & | ytab, | ||
| const Tbl & | ztab, | ||
| const Tbl & | ftab, | ||
| const Tbl & | dfdytab, | ||
| const Tbl & | dfdztab, | ||
| const Tbl & | d2fdydztab, | ||
| const double | y, | ||
| const double | z, | ||
| double & | f, | ||
| double & | dfdy, | ||
| double & | dfdz | ||
| ) | const |
Routine used by interpol_3d_bifluid to perform the 2D interpolation on the chemical potentials on each slice of constant 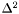 .
.
This method is based on the routine interpol_herm_2d but is adapted to the use of 3D tables.
Definition at line 1839 of file eos_bf_tabul.C.
References Lorene::Tbl::dim.
◆ interpol_3d_bifluid()
| void Lorene::Eos_bf_tabul::interpol_3d_bifluid | ( | const double | delta2, |
| const double | mu1, | ||
| const double | mu2, | ||
| double & | press, | ||
| double & | nbar1, | ||
| double & | nbar2, | ||
| double & | alpha | ||
| ) | const |
General method computing the pressure, both baryon densities and alpha from the values of both chemical potentials and the relative speed at the point under consideration.
This routine uses the following 3D interpolation scheme from tabulated EoSs :
- Hermite interpolation on the chemical potentials,
- linear interpolation in the relative speed.
- Parameters
-
delta2 [input] the relative velocity field 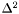
mu1 [input] chemical potential of 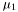 of fluid 1
of fluid 1 mu2 [input] chemical potential of 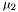 of fluid 2
of fluid 2press [output] generalized pressure p
nbar1 [output] baryonic density of the first fluid nbar2 [output] baryonic density of the second fluid
alpha [output] 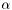
Definition at line 1298 of file eos_bf_tabul.C.
References d2psdmu1dmu2_tab, delta_car_tab, dn1sddelta_car_tab, dn2sddelta_car_tab, dpsddelta_car_tab, interpol_2d_Tbl3d(), Lorene::Eos_bifluid::m_1, Lorene::Eos_bifluid::m_2, mu1_tab, mu2_tab, n1_tab, n2_tab, press_tab, and Lorene::Tbl::set_etat_zero().
◆ nbar_ent()
|
inherited |
Computes both baryon density fields from the log-enthalpy fields and the relative velocity.
- Parameters
-
ent1 [input, unit:  ] log-enthalpy
] log-enthalpy 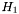
ent2 [input, unit:  ] log-enthalpy
] log-enthalpy 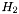
delta2 [input, unit:  ] relative velocity
] relative velocity 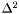
nbar1 [output] baryonic density of the first fluid nbar2 [output] baryonic density of the second fluid [unit:  ]
] nzet number of domains where the baryon density is to be computed. l_min index of the innermost domain is which the baryon density is to be computed [default value: 0]; the baryon density is computed only in domains whose indices are in [l_min,l_min+nzet-1] . In the other domains, it is set to zero.
Definition at line 416 of file eos_bifluid.C.
References Lorene::Cmp::get_etat().
◆ nbar_ent_p()
|
virtual |
Computes both baryon densities from the log-enthalpies.
- Parameters
-
ent1 [input, unit:  ] log-enthalpy
] log-enthalpy 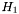
ent2 [input, unit:  ] log-enthalpy
] log-enthalpy 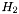
delta2 [input, unit:  ] relative velocity
] relative velocity 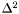
nbar1 [output] baryonic density of the first fluid nbar2 [output] baryonic density of the second fluid [unit:  ]
]
Implements Lorene::Eos_bifluid.
Definition at line 943 of file eos_bf_tabul.C.
References delta_car_max, delta_car_min, Lorene::exp(), interpol_3d_bifluid(), Lorene::Eos_bifluid::m_1, Lorene::Eos_bifluid::m_2, mu1_max, and mu2_max.
◆ nbar_ent_p1()
|
virtual |
Computes baryon density out of the log-enthalpy asuming that only fluid 1 is present.
- Parameters
-
ent1 [input, unit:  ] log-enthalpy
] log-enthalpy 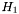
- Returns
- nbar1 baryonic density of the first fluid
Implements Lorene::Eos_bifluid.
Definition at line 1009 of file eos_bf_tabul.C.
References Lorene::c_est_pas_fait().
◆ nbar_ent_p2()
|
virtual |
Computes baryon density out of the log-enthalpy assuming that only fluid 2 is present.
- Parameters
-
ent2 [input, unit:  ] log-enthalpy
] log-enthalpy 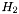
- Returns
- nbar2 baryonic density of the second fluid
Implements Lorene::Eos_bifluid.
Definition at line 1034 of file eos_bf_tabul.C.
References Lorene::c_est_pas_fait().
◆ operator!=()
|
virtual |
Comparison operator (difference)
Implements Lorene::Eos_bifluid.
Definition at line 267 of file eos_bf_tabul.C.
References operator==().
◆ operator=()
|
private |
Assignment to another Eos_bf_tabul.
Definition at line 177 of file eos_bf_tabul.C.
References d2psdmu1dmu2_tab, delta_car_max, delta_car_min, delta_car_tab, dn1sddelta_car_tab, dn2sddelta_car_tab, dpsddelta_car_tab, mu1_max, mu1_min, mu1_tab, mu2_max, mu2_min, mu2_tab, n1_tab, n2_tab, Lorene::Eos_bifluid::operator=(), press_tab, and tablename.
◆ operator==()
|
virtual |
Comparison operator (egality)
Implements Lorene::Eos_bifluid.
Definition at line 244 of file eos_bf_tabul.C.
References Lorene::Eos_bifluid::identify(), identify(), and tablename.
◆ operator>>()
|
protectedvirtual |
Operator >>
Implements Lorene::Eos_bifluid.
Definition at line 229 of file eos_bf_tabul.C.
References tablename.
◆ press_ent()
|
inherited |
Computes the pressure from the log-enthalpy fields and the relative velocity.
- Parameters
-
ent1 [input, unit:  ] log-enthalpy
] log-enthalpy 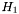
ent2 [input, unit:  ] log-enthalpy
] log-enthalpy 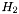
delta2 [input, unit:  ] relative velocity
] relative velocity 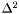
nzet number of domains where the pressure is to be computed. l_min index of the innermost domain is which the pressure is to be computed [default value: 0]; the pressure is computed only in domains whose indices are in [l_min,l_min+nzet-1] . In the other domains, it is set to zero.
- Returns
- pressure field [unit:
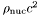 ], where
], where 
Definition at line 584 of file eos_bifluid.C.
References Lorene::Cmp::get_etat(), and Lorene::Cmp::get_mp().
◆ press_ent_p()
|
virtual |
Computes the pressure from the baryonic log-enthalpies and the relative velocity.
Computes the pressure from the log-enthalpy.
- Parameters
-
ent1 [input, unit:  ] log-enthalpy
] log-enthalpy 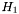 of fluid 1
of fluid 1 ent2 [input, unit:  ] log-enthalpy
] log-enthalpy 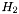 of fluid 2
of fluid 2 delta2 [input, unit:  ] relative velocity
] relative velocity 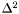
- Returns
- pressure p [unit:
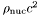 ], where
], where 
Definition at line 1087 of file eos_bf_tabul.C.
References delta_car_max, delta_car_min, Lorene::exp(), interpol_3d_bifluid(), Lorene::Eos_bifluid::m_1, Lorene::Eos_bifluid::m_2, mu1_max, and mu2_max.
◆ press_nbar_p()
|
virtual |
Computes the pressure from the baryonic densities and the relative velocity.
- Parameters
-
nbar1 [input] baryonic density of the first fluid nbar2 [input] baryonic density of the second fluid [unit:  ]
] delta2 [input, unit:  ] relative velocity
] relative velocity 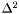
- Returns
- pressure p [unit:
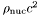 ], where
], where 
Implements Lorene::Eos_bifluid.
Definition at line 1073 of file eos_bf_tabul.C.
References Lorene::c_est_pas_fait().
◆ read_table()
|
protected |
Reads the file containing the table and initializes the arrays mu1_tab, mu2_tab, delta_car_tab, press_tab, n1_tab, n2_tab, c\ d2psdmu1dmu2_tab , c\ dpsddelta_car_tab, c\ dn1sddelta_car_tab, c\ dn2sddelta_car_tab.
Definition at line 279 of file eos_bf_tabul.C.
References authors, d2psdmu1dmu2_tab, delta_car_max, delta_car_min, delta_car_tab, dn1sddelta_car_tab, dn2sddelta_car_tab, dpsddelta_car_tab, mu1_max, mu1_min, mu1_tab, mu2_max, mu2_min, mu2_tab, n1_tab, n2_tab, Lorene::pow(), press_tab, Lorene::Tbl::set(), Lorene::Tbl::set_etat_qcq(), and tablename.
◆ sauve()
|
virtual |
Save in a file.
Reimplemented from Lorene::Eos_bifluid.
Definition at line 218 of file eos_bf_tabul.C.
References Lorene::Eos_bifluid::sauve(), and tablename.
◆ trans2Eos()
|
virtual |
Makes a translation from Eos_bifluid to Eos .
This is only useful for the construction of a Et_rot_bifluid star and ought not to be used in other situations.
Implements Lorene::Eos_bifluid.
Definition at line 1948 of file eos_bf_tabul.C.
Friends And Related Function Documentation
◆ Eos_bifluid::eos_from_file
|
friend |
The construction functions from a file.
Member Data Documentation
◆ authors
|
protected |
Authors.
Definition at line 1446 of file eos_bifluid.h.
◆ d2psdmu1dmu2_tab
|
protected |
Table of 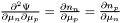 .
.
Definition at line 1485 of file eos_bifluid.h.
◆ delta_car_max
|
protected |
Upper boundary of the relative velocity interval.
Definition at line 1452 of file eos_bifluid.h.
◆ delta_car_min
|
protected |
Lower boundary of the relative velocity interval.
Definition at line 1449 of file eos_bifluid.h.
◆ delta_car_tab
|
protected |
Table of 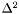 .
.
Definition at line 1473 of file eos_bifluid.h.
◆ dn1sddelta_car_tab
|
protected |
Table of 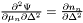 .
.
Definition at line 1491 of file eos_bifluid.h.
◆ dn2sddelta_car_tab
|
protected |
Table of 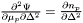 .
.
Definition at line 1494 of file eos_bifluid.h.
◆ dpsddelta_car_tab
|
protected |
Table of 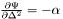 .
.
Definition at line 1488 of file eos_bifluid.h.
◆ m_1
|
protectedinherited |
Individual particle mass 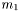
[unit:  ].
].
Definition at line 191 of file eos_bifluid.h.
◆ m_2
|
protectedinherited |
Individual particle mass 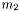
[unit:  ].
].
Definition at line 196 of file eos_bifluid.h.
◆ mu1_max
|
protected |
Upper boundary of the chemical-potential interval (fluid 1 = n)
Definition at line 1458 of file eos_bifluid.h.
◆ mu1_min
|
protected |
Lower boundary of the chemical-potential interval (fluid 1 = n)
Definition at line 1455 of file eos_bifluid.h.
◆ mu1_tab
|
protected |
Table of 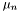 where
where 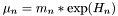 .
.
Definition at line 1467 of file eos_bifluid.h.
◆ mu2_max
|
protected |
Upper boundary of the chemical-potential interval (fluid 2 = p)
Definition at line 1464 of file eos_bifluid.h.
◆ mu2_min
|
protected |
Lower boundary of the chemical-potential interval (fluid 2 = p)
Definition at line 1461 of file eos_bifluid.h.
◆ mu2_tab
|
protected |
Table of 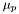 where
where 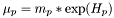 .
.
Definition at line 1470 of file eos_bifluid.h.
◆ n1_tab
|
protected |
Table of 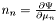 .
.
Definition at line 1479 of file eos_bifluid.h.
◆ n2_tab
|
protected |
Table of 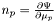 .
.
Definition at line 1482 of file eos_bifluid.h.
◆ name
|
protectedinherited |
EOS name.
Definition at line 186 of file eos_bifluid.h.
◆ press_tab
|
protected |
Table of 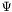 .
.
Definition at line 1476 of file eos_bifluid.h.
◆ tablename
|
protected |
Name of the file containing the tabulated data (be careful, Eos_bifluid uses char*)
Definition at line 1443 of file eos_bifluid.h.
The documentation for this class was generated from the following files:
