Polytropic equation of state (relativistic case). More...
#include <eos.h>
Public Member Functions | |
| Eos_poly (double gamma, double kappa) | |
Standard constructor (sets both m_0 and mu_0 to 1). More... | |
| Eos_poly (double gamma, double kappa, double mass) | |
Standard constructor with individual particle mass (sets mu_0 to 1). More... | |
| Eos_poly (double gamma, double kappa, double mass, double mu_zero) | |
| Standard constructor with individual particle mass and zero-pressure chemical potential. More... | |
| Eos_poly (const Eos_poly &) | |
| Copy constructor. More... | |
| virtual | ~Eos_poly () |
| Destructor. More... | |
| void | operator= (const Eos_poly &) |
Assignment to another Eos_poly. More... | |
| virtual bool | operator== (const Eos &) const |
| Comparison operator (egality) More... | |
| virtual bool | operator!= (const Eos &) const |
| Comparison operator (difference) More... | |
| virtual int | identify () const |
Returns a number to identify the sub-classe of Eos the object belongs to. More... | |
| double | get_gam () const |
Returns the adiabatic index  (cf. Eq. (3)) More... (cf. Eq. (3)) More... | |
| double | get_kap () const |
Returns the pressure coefficient 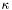 (cf. More... (cf. More... | |
| double | get_m_0 () const |
Return the individual particule mass 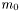 (cf. More... (cf. More... | |
| double | get_mu_0 () const |
Return the relativistic chemical potential at zero pressure [unit: 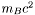 , with , with  ]. More... ]. More... | |
| virtual void | sauve (FILE *) const |
| Save in a file. More... | |
| virtual double | nbar_ent_p (double ent, const Param *par=0x0) const |
| Computes the baryon density from the log-enthalpy. More... | |
| virtual double | ener_ent_p (double ent, const Param *par=0x0) const |
| Computes the total energy density from the log-enthalpy. More... | |
| virtual double | press_ent_p (double ent, const Param *par=0x0) const |
| Computes the pressure from the log-enthalpy. More... | |
| virtual double | der_nbar_ent_p (double ent, const Param *par=0x0) const |
Computes the logarithmic derivative 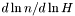 from the log-enthalpy. More... from the log-enthalpy. More... | |
| virtual double | der_ener_ent_p (double ent, const Param *par=0x0) const |
Computes the logarithmic derivative 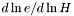 from the log-enthalpy. More... from the log-enthalpy. More... | |
| virtual double | der_press_ent_p (double ent, const Param *par=0x0) const |
Computes the logarithmic derivative 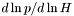 from the log-enthalpy. More... from the log-enthalpy. More... | |
| virtual double | csound_square_ent_p (double ent, const Param *par=0x0) const |
Computes the sound speed squared 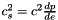 from the enthapy with extra parameters (virtual function implemented in the derived classes). More... from the enthapy with extra parameters (virtual function implemented in the derived classes). More... | |
| const char * | get_name () const |
| Returns the EOS name. More... | |
| void | set_name (const char *name_i) |
| Sets the EOS name. More... | |
| Cmp | nbar_ent (const Cmp &ent, int nzet, int l_min=0, Param *par=0x0) const |
| Computes the baryon density field from the log-enthalpy field and extra parameters. More... | |
| Scalar | nbar_ent (const Scalar &ent, int nzet, int l_min=0, Param *par=0x0) const |
| Computes the baryon density field from the log-enthalpy field and extra parameters. More... | |
| Cmp | ener_ent (const Cmp &ent, int nzet, int l_min=0, Param *par=0x0) const |
| Computes the total energy density from the log-enthalpy and extra parameters. More... | |
| Scalar | ener_ent (const Scalar &ent, int nzet, int l_min=0, Param *par=0x0) const |
| Computes the total energy density from the log-enthalpy and extra parameters. More... | |
| Cmp | press_ent (const Cmp &ent, int nzet, int l_min=0, Param *par=0x0) const |
| Computes the pressure from the log-enthalpy and extra parameters. More... | |
| Scalar | press_ent (const Scalar &ent, int nzet, int l_min=0, Param *par=0x0) const |
| Computes the pressure from the log-enthalpy and extra parameters. More... | |
| Cmp | der_nbar_ent (const Cmp &ent, int nzet, int l_min=0, Param *par=0x0) const |
Computes the logarithmic derivative 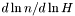 from the log-enthalpy and extra parameters. More... from the log-enthalpy and extra parameters. More... | |
| Scalar | der_nbar_ent (const Scalar &ent, int nzet, int l_min=0, Param *par=0x0) const |
Computes the logarithmic derivative 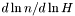 from the log-enthalpy and extra parameters. More... from the log-enthalpy and extra parameters. More... | |
| Cmp | der_ener_ent (const Cmp &ent, int nzet, int l_min=0, Param *par=0x0) const |
Computes the logarithmic derivative 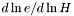 from the log-enthalpy and extra parameters. More... from the log-enthalpy and extra parameters. More... | |
| Scalar | der_ener_ent (const Scalar &ent, int nzet, int l_min=0, Param *par=0x0) const |
Computes the logarithmic derivative 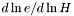 from the log-enthalpy and extra parameters. More... from the log-enthalpy and extra parameters. More... | |
| Cmp | der_press_ent (const Cmp &ent, int nzet, int l_min=0, Param *par=0x0) const |
Computes the logarithmic derivative 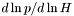 from the log-enthalpy and extra parameters. More... from the log-enthalpy and extra parameters. More... | |
| Scalar | der_press_ent (const Scalar &ent, int nzet, int l_min=0, Param *par=0x0) const |
Computes the logarithmic derivative 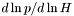 from the log-enthalpy and extra parameters. More... from the log-enthalpy and extra parameters. More... | |
| Scalar | csound_square_ent (const Scalar &ent, int nzet, int l_min=0, Param *par=0x0) const |
Computes the sound speed squared 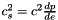 from the enthalpy with extra parameters. More... from the enthalpy with extra parameters. More... | |
Static Public Member Functions | |
| static Eos * | eos_from_file (FILE *) |
| Construction of an EOS from a binary file. More... | |
| static Eos * | eos_from_file (ifstream &) |
| Construction of an EOS from a formatted file. More... | |
Protected Member Functions | |
| Eos_poly (FILE *) | |
Constructor from a binary file (created by the function sauve(FILE*) ). More... | |
| Eos_poly (ifstream &) | |
| Constructor from a formatted file. More... | |
| void | set_auxiliary () |
Computes the auxiliary quantities gam1 , unsgam1 , gam1sgamkap from the values of gam and kap. More... | |
| virtual ostream & | operator>> (ostream &) const |
| Operator >> More... | |
| void | calcule (const Cmp &thermo, int nzet, int l_min, double(Eos::*fait)(double, const Param *) const, Param *par, Cmp &resu) const |
General computational method for Cmp 's. More... | |
| void | calcule (const Scalar &thermo, int nzet, int l_min, double(Eos::*fait)(double, const Param *) const, Param *par, Scalar &resu) const |
General computational method for Scalar 's. More... | |
Protected Attributes | |
| double | gam |
Adiabatic index  (cf. Eq. (3)) More... (cf. Eq. (3)) More... | |
| double | kap |
Pressure coefficient 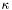 (cf. More... (cf. More... | |
| double | m_0 |
Individual particule mass 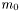 (cf. More... (cf. More... | |
| double | mu_0 |
Relativistic chemical potential at zero pressure [unit: 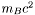 , with , with  ]. More... ]. More... | |
| double | gam1 |
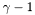 More... More... | |
| double | unsgam1 |
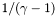 More... More... | |
| double | gam1sgamkap |
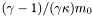 More... More... | |
| double | rel_mu_0 |
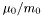 More... More... | |
| double | ent_0 |
Enthalpy at zero pressure ( 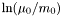 ) More... ) More... | |
| char | name [100] |
| EOS name. More... | |
Friends | |
| Eos * | Eos::eos_from_file (FILE *) |
| The construction functions from a file. More... | |
| Eos * | Eos::eos_from_file (ifstream &) |
Detailed Description
Polytropic equation of state (relativistic case).
This equation of state (EOS) corresponds to identical relativistic particles of rest mass is 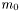 , whose total energy density e is related to their numerical density n by
, whose total energy density e is related to their numerical density n by
![\[ e(n) = {\kappa \over \gamma-1} n^\gamma + \mu_0 \, n \ , \qquad \qquad (1) \]](form_917.png)
where 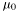 is the chemical potential at zero pressure. The relativistic (i.e. including rest mass energy) chemical potential is then
is the chemical potential at zero pressure. The relativistic (i.e. including rest mass energy) chemical potential is then
![\[ \mu(n) := {de\over dn} = {\kappa \gamma \over \gamma-1} n^{\gamma-1} + \mu_0 \ .\qquad \qquad (2) \]](form_918.png)
The pressure is given by the (zero-temperature) First Law of Thermodynamics: 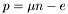 , so that
, so that
![\[ p(n) = \kappa n^\gamma \ . \qquad \qquad (3) \]](form_919.png)
The log-enthalpy is defined as the logarithm of the ratio of the enthalpy par particle by the partical rest mass energy :
![\[ H(n) := c^2 \ln \left( {e+p \over m_0 c^2\, n} \right) \ . \qquad \qquad (4) \]](form_920.png)
According to the (zero-temperature) First Law of Thermodynamics, the log-enthalpy is related to the chemical potential by
![\[ H = c^2 \ln \left( {\mu \over m_0 c^2} \right) \ . \qquad \qquad (5) \]](form_921.png)
From this expression and relation (2), the expression of the particle density in term of the log-enthalpy is
![\[ n(H) = \left[ {\gamma-1\over \gamma} {m_0 c^2 \over \kappa} \left( \exp(H) - {\mu_0\over m_0 c^2} \right) \right] ^{1/(\gamma-1)} \ . \qquad \qquad (6) \]](form_922.png)
The energy density and pressure as functions of H can then be obtained by inserting this relation into Eqs. (1) and (3).
()
Constructor & Destructor Documentation
◆ Eos_poly() [1/6]
| Lorene::Eos_poly::Eos_poly | ( | double | gamma, |
| double | kappa | ||
| ) |
Standard constructor (sets both m_0 and mu_0 to 1).
The individual particle mass 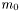 is set to the mean baryon mass
is set to the mean baryon mass  .
.
- Parameters
-
gamma adiabatic index  (cf. Eq. (3))
(cf. Eq. (3)) kappa pressure coefficient 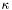
(cf. Eq. (3)) [unit: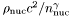 ], where
], where  and
and 
Definition at line 141 of file eos_poly.C.
References set_auxiliary().
◆ Eos_poly() [2/6]
| Lorene::Eos_poly::Eos_poly | ( | double | gamma, |
| double | kappa, | ||
| double | mass | ||
| ) |
Standard constructor with individual particle mass (sets mu_0 to 1).
- Parameters
-
gamma adiabatic index  (cf. Eq. (3))
(cf. Eq. (3)) kappa pressure coefficient 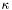 (cf. Eq. (3)) [unit:
(cf. Eq. (3)) [unit: 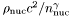 ], where
], where  and
and 
mass individual particule mass 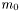 (cf. Eq. (1) [unit:
(cf. Eq. (1) [unit:  ]
]
Definition at line 151 of file eos_poly.C.
References set_auxiliary().
◆ Eos_poly() [3/6]
| Lorene::Eos_poly::Eos_poly | ( | double | gamma, |
| double | kappa, | ||
| double | mass, | ||
| double | mu_zero | ||
| ) |
Standard constructor with individual particle mass and zero-pressure chemical potential.
- Parameters
-
gamma adiabatic index  (cf. Eq. (3))
(cf. Eq. (3)) kappa pressure coefficient 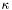 (cf. Eq. (3)) [unit:
(cf. Eq. (3)) [unit: 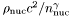 ], where
], where  and
and 
mass individual particule mass 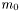 (cf. Eq. (1)) [unit:
(cf. Eq. (1)) [unit:  ]
] mu_zero Relativistic chemical potential at zero pressure [unit: 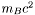 , with
, with  ]. (standard value: 1)
]. (standard value: 1)
Definition at line 161 of file eos_poly.C.
References set_auxiliary().
◆ Eos_poly() [4/6]
| Lorene::Eos_poly::Eos_poly | ( | const Eos_poly & | eosi | ) |
◆ Eos_poly() [5/6]
|
protected |
Constructor from a binary file (created by the function sauve(FILE*) ).
This constructor is protected because any EOS construction from a binary file must be done via the function Eos::eos_from_file(FILE*) .
Definition at line 182 of file eos_poly.C.
References Lorene::fread_be(), gam, kap, m_0, mu_0, and set_auxiliary().
◆ Eos_poly() [6/6]
|
protected |
Constructor from a formatted file.
This constructor is protected because any EOS construction from a formatted file must be done via the function Eos::eos_from_file(ifstream&) .
Definition at line 205 of file eos_poly.C.
References gam, kap, m_0, mu_0, and set_auxiliary().
◆ ~Eos_poly()
|
virtual |
Destructor.
Definition at line 230 of file eos_poly.C.
Member Function Documentation
◆ calcule() [1/2]
|
protectedinherited |
General computational method for Cmp 's.
- Parameters
-
thermo [input] thermodynamical quantity (for instance the enthalpy field)from which the thermodynamical quantity resuis to be computed.nzet [input] number of domains where resuis to be computed.l_min [input] index of the innermost domain is which resuis to be computed [default value: 0];resuis computed only in domains whose indices are in[l_min,l_min+nzet-1] . In the other domains, it is set to zero.fait [input] pointer on the member function of class Eoswhich performs the pointwise calculation.par possible extra parameters of the EOS resu [output] result of the computation.
Definition at line 213 of file eos.C.
References Lorene::Cmp::get_etat().
◆ calcule() [2/2]
|
protectedinherited |
General computational method for Scalar 's.
- Parameters
-
thermo [input] thermodynamical quantity (for instance the enthalpy field)from which the thermodynamical quantity resuis to be computed.nzet [input] number of domains where resuis to be computed.l_min [input] index of the innermost domain is which resuis to be computed [default value: 0];resuis computed only in domains whose indices are in[l_min,l_min+nzet-1] . In the other domains, it is set to zero.fait [input] pointer on the member function of class Eoswhich performs the pointwise calculation.par possible extra parameters of the EOS resu [output] result of the computation.
Definition at line 285 of file eos.C.
References Lorene::Scalar::get_etat().
◆ csound_square_ent()
|
inherited |
Computes the sound speed squared 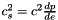 from the enthalpy with extra parameters.
from the enthalpy with extra parameters.
- Parameters
-
ent [input, unit: c^2] enthalpy nzet number of domains where the derivative dln(e)/dln(H) is to be computed. l_min index of the innermost domain is which the coefficient dln(n)/dln(H) is to be computed [default value: 0]; the derivative dln(e)/dln(H) is computed only in domains whose indices are in [l_min,l_min+nzet-1] . In the other domains, it is set to zero.par possible extra parameters of the EOS
- Returns
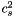 [unit: c^2]
[unit: c^2]
Definition at line 499 of file eos.C.
References Lorene::Eos::calcule(), Lorene::Eos::csound_square_ent_p(), and Lorene::Tensor::get_mp().
◆ csound_square_ent_p()
|
virtual |
Computes the sound speed squared 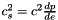 from the enthapy with extra parameters (virtual function implemented in the derived classes).
from the enthapy with extra parameters (virtual function implemented in the derived classes).
- Parameters
-
ent [input, unit: c^2] enthalpy par possible extra parameters of the EOS
- Returns
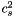 [unit: c^2]
[unit: c^2]
Implements Lorene::Eos.
Reimplemented in Lorene::Eos_poly_newt.
Definition at line 469 of file eos_poly.C.
◆ der_ener_ent() [1/2]
|
inherited |
Computes the logarithmic derivative 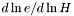 from the log-enthalpy and extra parameters.
from the log-enthalpy and extra parameters.
- Parameters
-
ent [input, unit:  ] log-enthalpy H defined by
] log-enthalpy H defined by 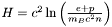 , where e is the (total) energy density, p the pressure, n the baryon density, and
, where e is the (total) energy density, p the pressure, n the baryon density, and 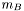 the baryon mass
the baryon mass nzet number of domains where the derivative dln(e)/dln(H) is to be computed. l_min index of the innermost domain is which the coefficient dln(n)/dln(H) is to be computed [default value: 0]; the derivative dln(e)/dln(H) is computed only in domains whose indices are in [l_min,l_min+nzet-1] . In the other domains, it is set to zero.par possible extra parameters of the EOS
- Returns
- dln(e)/dln(H)
Definition at line 454 of file eos.C.
References Lorene::Eos::calcule(), Lorene::Eos::der_ener_ent_p(), and Lorene::Cmp::get_mp().
◆ der_ener_ent() [2/2]
|
inherited |
Computes the logarithmic derivative 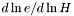 from the log-enthalpy and extra parameters.
from the log-enthalpy and extra parameters.
- Parameters
-
ent [input, unit:  ] log-enthalpy H defined by
] log-enthalpy H defined by 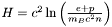 , where e is the (total) energy density, p the pressure, n the baryon density, and
, where e is the (total) energy density, p the pressure, n the baryon density, and 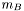 the baryon mass
the baryon mass nzet number of domains where the derivative dln(e)/dln(H) is to be computed. l_min index of the innermost domain is which the coefficient dln(n)/dln(H) is to be computed [default value: 0]; the derivative dln(e)/dln(H) is computed only in domains whose indices are in [l_min,l_min+nzet-1] . In the other domains, it is set to zero.par possible extra parameters of the EOS
- Returns
- dln(e)/dln(H)
Definition at line 464 of file eos.C.
References Lorene::Eos::calcule(), Lorene::Eos::der_ener_ent_p(), and Lorene::Tensor::get_mp().
◆ der_ener_ent_p()
|
virtual |
Computes the logarithmic derivative 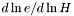 from the log-enthalpy.
from the log-enthalpy.
- Parameters
-
ent [input, unit:  ] log-enthalpy H defined by Eq. (4)
] log-enthalpy H defined by Eq. (4)par possible extra parameters of the EOS
- Returns
- dln(e)/dln(H)
Implements Lorene::Eos.
Reimplemented in Lorene::Eos_poly_newt.
Definition at line 436 of file eos_poly.C.
References ent_0, gam, gam1, kap, mu_0, nbar_ent_p(), Lorene::pow(), and unsgam1.
◆ der_nbar_ent() [1/2]
|
inherited |
Computes the logarithmic derivative 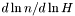 from the log-enthalpy and extra parameters.
from the log-enthalpy and extra parameters.
- Parameters
-
ent [input, unit:  ] log-enthalpy H defined by
] log-enthalpy H defined by 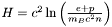 , where e is the (total) energy density, p the pressure, n the baryon density, and
, where e is the (total) energy density, p the pressure, n the baryon density, and 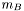 the baryon mass
the baryon mass nzet number of domains where the derivative dln(n)/dln(H) is to be computed. l_min index of the innermost domain is which the coefficient dln(n)/dln(H) is to be computed [default value: 0]; the derivative dln(n)/dln(H) is computed only in domains whose indices are in [l_min,l_min+nzet-1] . In the other domains, it is set to zero.par possible extra parameters of the EOS
- Returns
- dln(n)/dln(H)
Definition at line 431 of file eos.C.
References Lorene::Eos::calcule(), Lorene::Eos::der_nbar_ent_p(), and Lorene::Cmp::get_mp().
◆ der_nbar_ent() [2/2]
|
inherited |
Computes the logarithmic derivative 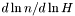 from the log-enthalpy and extra parameters.
from the log-enthalpy and extra parameters.
- Parameters
-
ent [input, unit:  ] log-enthalpy H defined by
] log-enthalpy H defined by 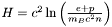 , where e is the (total) energy density, p the pressure, n the baryon density, and
, where e is the (total) energy density, p the pressure, n the baryon density, and 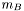 the baryon mass
the baryon mass nzet number of domains where the derivative dln(n)/dln(H) is to be computed. l_min index of the innermost domain is which the coefficient dln(n)/dln(H) is to be computed [default value: 0]; the derivative dln(n)/dln(H) is computed only in domains whose indices are in [l_min,l_min+nzet-1] . In the other domains, it is set to zero.par possible extra parameters of the EOS
- Returns
- dln(n)/dln(H)
Definition at line 441 of file eos.C.
References Lorene::Eos::calcule(), Lorene::Eos::der_nbar_ent_p(), and Lorene::Tensor::get_mp().
◆ der_nbar_ent_p()
|
virtual |
Computes the logarithmic derivative 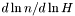 from the log-enthalpy.
from the log-enthalpy.
- Parameters
-
ent [input, unit:  ] log-enthalpy H defined by Eq. (4)
] log-enthalpy H defined by Eq. (4)par possible extra parameters of the EOS
- Returns
- dln(n)/dln(H)
Implements Lorene::Eos.
Reimplemented in Lorene::Eos_poly_newt.
Definition at line 421 of file eos_poly.C.
◆ der_press_ent() [1/2]
|
inherited |
Computes the logarithmic derivative 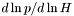 from the log-enthalpy and extra parameters.
from the log-enthalpy and extra parameters.
- Parameters
-
ent [input, unit:  ] log-enthalpy H defined by
] log-enthalpy H defined by 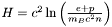 , where e is the (total) energy density, p the pressure, n the baryon density, and
, where e is the (total) energy density, p the pressure, n the baryon density, and 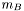 the baryon mass
the baryon mass nzet number of domains where the derivative dln(p)/dln(H) is to be computed. par possible extra parameters of the EOS l_min index of the innermost domain is which the coefficient dln(n)/dln(H) is to be computed [default value: 0]; the derivative dln(p)/dln(H) is computed only in domains whose indices are in [l_min,l_min+nzet-1] . In the other domains, it is set to zero.
- Returns
- dln(p)/dln(H)
Definition at line 476 of file eos.C.
References Lorene::Eos::calcule(), Lorene::Eos::der_press_ent_p(), and Lorene::Cmp::get_mp().
◆ der_press_ent() [2/2]
|
inherited |
Computes the logarithmic derivative 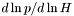 from the log-enthalpy and extra parameters.
from the log-enthalpy and extra parameters.
- Parameters
-
ent [input, unit:  ] log-enthalpy H defined by
] log-enthalpy H defined by 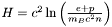 , where e is the (total) energy density, p the pressure, n the baryon density, and
, where e is the (total) energy density, p the pressure, n the baryon density, and 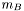 the baryon mass
the baryon mass nzet number of domains where the derivative dln(p)/dln(H) is to be computed. par possible extra parameters of the EOS l_min index of the innermost domain is which the coefficient dln(n)/dln(H) is to be computed [default value: 0]; the derivative dln(p)/dln(H) is computed only in domains whose indices are in [l_min,l_min+nzet-1] . In the other domains, it is set to zero.
- Returns
- dln(p)/dln(H)
Definition at line 486 of file eos.C.
References Lorene::Eos::calcule(), Lorene::Eos::der_press_ent_p(), and Lorene::Tensor::get_mp().
◆ der_press_ent_p()
|
virtual |
Computes the logarithmic derivative 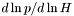 from the log-enthalpy.
from the log-enthalpy.
- Parameters
-
ent [input, unit:  ] log-enthalpy H defined by Eq. (4)
] log-enthalpy H defined by Eq. (4)par possible extra parameters of the EOS
- Returns
- dln(p)/dln(H)
Implements Lorene::Eos.
Reimplemented in Lorene::Eos_poly_newt.
Definition at line 455 of file eos_poly.C.
◆ ener_ent() [1/2]
|
inherited |
Computes the total energy density from the log-enthalpy and extra parameters.
- Parameters
-
ent [input, unit:  ] log-enthalpy H defined by
] log-enthalpy H defined by 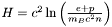 , where e is the (total) energy density, p the pressure, n the baryon density, and
, where e is the (total) energy density, p the pressure, n the baryon density, and 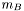 the baryon mass
the baryon mass nzet number of domains where the energy density is to be computed. l_min index of the innermost domain is which the energy density is to be computed [default value: 0]; the energy density is computed only in domains whose indices are in [l_min,l_min+nzet-1] . In the other domains, it is set to zero.par possible extra parameters of the EOS
- Returns
- energy density [unit:
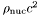 ], where
], where 
Definition at line 387 of file eos.C.
References Lorene::Eos::calcule(), Lorene::Eos::ener_ent_p(), and Lorene::Cmp::get_mp().
◆ ener_ent() [2/2]
|
inherited |
Computes the total energy density from the log-enthalpy and extra parameters.
- Parameters
-
ent [input, unit:  ] log-enthalpy H defined by
] log-enthalpy H defined by 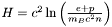 , where e is the (total) energy density, p the pressure, n the baryon density, and
, where e is the (total) energy density, p the pressure, n the baryon density, and 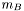 the baryon mass
the baryon mass nzet number of domains where the energy density is to be computed. l_min index of the innermost domain is which the energy density is to be computed [default value: 0]; the energy density is computed only in domains whose indices are in [l_min,l_min+nzet-1] . In the other domains, it is set to zero.par possible extra parameters of the EOS
- Returns
- energy density [unit:
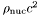 ], where
], where 
Definition at line 397 of file eos.C.
References Lorene::Eos::calcule(), Lorene::Eos::ener_ent_p(), and Lorene::Tensor::get_mp().
◆ ener_ent_p()
|
virtual |
Computes the total energy density from the log-enthalpy.
- Parameters
-
ent [input, unit:  ] log-enthalpy H defined by Eq. (4)
] log-enthalpy H defined by Eq. (4)par possible extra parameters of the EOS
- Returns
- energy density e [unit:
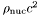 ], where
], where 
Implements Lorene::Eos.
Reimplemented in Lorene::Eos_poly_newt.
Definition at line 398 of file eos_poly.C.
References gam, kap, mu_0, nbar_ent_p(), Lorene::pow(), and unsgam1.
◆ eos_from_file() [1/2]
|
staticinherited |
Construction of an EOS from a binary file.
The file must have been created by the function sauve(FILE*) .
Definition at line 193 of file eos_from_file.C.
References Lorene::fread_be().
◆ eos_from_file() [2/2]
|
staticinherited |
Construction of an EOS from a formatted file.
The fist line of the file must start by the EOS number, according to the following conventions:
- 1 = relativistic polytropic EOS (class
Eos_poly). - 2 = Newtonian polytropic EOS (class
Eos_poly_newt). - 3 = Relativistic incompressible EOS (class
Eos_incomp). - 4 = Newtonian incompressible EOS (class
Eos_incomp_newt). - 5 = Strange matter (MIT Bag model)
- 6 = Strange matter (MIT Bag model) with crust
- 10 = SLy4 (Douchin & Haensel 2001)
- 11 = FPS (Friedman-Pandharipande + Skyrme) - 12 = BPAL12 (Bombaci et al. 1995)
- 13 = AkmalPR (Akmal, Pandharipande & Ravenhall 1998)
- 14 = BBB2 (Baldo, Bombaci & Burgio 1997)
- 15 = BalbN1H1 (Balberg 2000)
- 16 = GlendNH3 (Glendenning 1985, case 3)
- 17 = Tabulated EOS in CompOSE format
- 18 = magnetized (tabulated) equation of state
- 19 = relativistic ideal Fermi gas at zero temperature (class
Eos_Fermi) - 20 = Tabulated EOS in CompOSE format corrected for thermo. consistency
- 100 = Multi-domain EOS (class
MEos) - 110 = Multi-polytropic EOS (class
Eos_multi_poly) - 120 = Fitted SLy4 (Shibata 2004)
- 121 = Fitted FPS (Shibata 2004)
- 122 = Fitted AkmalPR (Taniguchi 2005)
The second line in the file should contain a name given by the user to the EOS. The following lines should contain the EOS parameters (one parameter per line), in the same order than in the class declaration.
Definition at line 345 of file eos_from_file.C.
◆ get_gam()
| double Lorene::Eos_poly::get_gam | ( | ) | const |
Returns the adiabatic index  (cf. Eq. (3))
(cf. Eq. (3))
Definition at line 271 of file eos_poly.C.
References gam.
◆ get_kap()
| double Lorene::Eos_poly::get_kap | ( | ) | const |
Returns the pressure coefficient 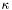 (cf.
(cf.
Eq. (3)) [unit: 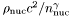 ], where
], where  and
and  .
.
Definition at line 275 of file eos_poly.C.
References kap.
◆ get_m_0()
| double Lorene::Eos_poly::get_m_0 | ( | ) | const |
Return the individual particule mass 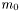 (cf.
(cf.
Eq. (1)) [unit:  ].
].
Definition at line 279 of file eos_poly.C.
References m_0.
◆ get_mu_0()
| double Lorene::Eos_poly::get_mu_0 | ( | ) | const |
Return the relativistic chemical potential at zero pressure [unit: 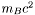 , with
, with  ].
].
Definition at line 283 of file eos_poly.C.
References mu_0.
◆ get_name()
|
inherited |
◆ identify()
|
virtual |
Returns a number to identify the sub-classe of Eos the object belongs to.
Implements Lorene::Eos.
Reimplemented in Lorene::Eos_poly_newt.
Definition at line 139 of file eos_from_file.C.
◆ nbar_ent() [1/2]
|
inherited |
Computes the baryon density field from the log-enthalpy field and extra parameters.
- Parameters
-
ent [input, unit:  ] log-enthalpy H defined by
] log-enthalpy H defined by 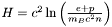 , where e is the (total) energy density, p the pressure, n the baryon density, and
, where e is the (total) energy density, p the pressure, n the baryon density, and 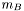 the baryon mass
the baryon mass nzet number of domains where the baryon density is to be computed. l_min index of the innermost domain is which the baryon density is to be computed [default value: 0]; the baryon density is computed only in domains whose indices are in [l_min,l_min+nzet-1] . In the other domains, it is set to zero.par possible extra parameters of the EOS
- Returns
- baryon density [unit:
 ]
]
Definition at line 362 of file eos.C.
References Lorene::Eos::calcule(), Lorene::Cmp::get_mp(), and Lorene::Eos::nbar_ent_p().
◆ nbar_ent() [2/2]
|
inherited |
Computes the baryon density field from the log-enthalpy field and extra parameters.
- Parameters
-
ent [input, unit:  ] log-enthalpy H defined by
] log-enthalpy H defined by 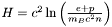 , where e is the (total) energy density, p the pressure, n the baryon density, and
, where e is the (total) energy density, p the pressure, n the baryon density, and 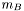 the baryon mass
the baryon mass nzet number of domains where the baryon density is to be computed. l_min index of the innermost domain is which the baryon density is to be computed [default value: 0]; the baryon density is computed only in domains whose indices are in [l_min,l_min+nzet-1] . In the other domains, it is set to zero.par possible extra parameters of the EOS
- Returns
- baryon density [unit:
 ]
]
Definition at line 372 of file eos.C.
References Lorene::Eos::calcule(), Lorene::Tensor::get_mp(), and Lorene::Eos::nbar_ent_p().
◆ nbar_ent_p()
|
virtual |
Computes the baryon density from the log-enthalpy.
- Parameters
-
ent [input, unit:  ] log-enthalpy H defined by Eq. (4)
] log-enthalpy H defined by Eq. (4)par possible extra parameters of the EOS
- Returns
- baryon density n [unit:
 ]
]
Implements Lorene::Eos.
Reimplemented in Lorene::Eos_poly_newt.
Definition at line 383 of file eos_poly.C.
References ent_0, gam1sgamkap, Lorene::pow(), rel_mu_0, and unsgam1.
◆ operator!=()
|
virtual |
Comparison operator (difference)
Implements Lorene::Eos.
Reimplemented in Lorene::Eos_poly_newt.
Definition at line 339 of file eos_poly.C.
References operator==().
◆ operator=()
| void Lorene::Eos_poly::operator= | ( | const Eos_poly & | eosi | ) |
Assignment to another Eos_poly.
Definition at line 239 of file eos_poly.C.
References gam, kap, m_0, mu_0, Lorene::Eos::name, set_auxiliary(), and Lorene::Eos::set_name().
◆ operator==()
|
virtual |
Comparison operator (egality)
Implements Lorene::Eos.
Reimplemented in Lorene::Eos_poly_newt.
Definition at line 293 of file eos_poly.C.
References gam, Lorene::Eos::identify(), identify(), kap, m_0, and mu_0.
◆ operator>>()
|
protectedvirtual |
Operator >>
Implements Lorene::Eos.
Reimplemented in Lorene::Eos_poly_newt.
Definition at line 362 of file eos_poly.C.
◆ press_ent() [1/2]
|
inherited |
Computes the pressure from the log-enthalpy and extra parameters.
- Parameters
-
ent [input, unit:  ] log-enthalpy H defined by
] log-enthalpy H defined by 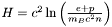 , where e is the (total) energy density, p the pressure, n the baryon density, and
, where e is the (total) energy density, p the pressure, n the baryon density, and 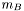 the baryon mass
the baryon mass nzet number of domains where the pressure is to be computed. l_min index of the innermost domain is which the pressure is to be computed [default value: 0]; the pressure is computed only in domains whose indices are in [l_min,l_min+nzet-1] . In the other domains, it is set to zero.par possible extra parameters of the EOS
- Returns
- pressure [unit:
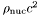 ], where
], where 
Definition at line 409 of file eos.C.
References Lorene::Eos::calcule(), Lorene::Cmp::get_mp(), and Lorene::Eos::press_ent_p().
◆ press_ent() [2/2]
|
inherited |
Computes the pressure from the log-enthalpy and extra parameters.
- Parameters
-
ent [input, unit:  ] log-enthalpy H defined by
] log-enthalpy H defined by 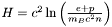 , where e is the (total) energy density, p the pressure, n the baryon density, and
, where e is the (total) energy density, p the pressure, n the baryon density, and 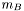 the baryon mass
the baryon mass nzet number of domains where the pressure is to be computed. l_min index of the innermost domain is which the pressure is to be computed [default value: 0]; the pressure is computed only in domains whose indices are in [l_min,l_min+nzet-1] . In the other domains, it is set to zero.par possible extra parameters of the EOS
- Returns
- pressure [unit:
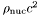 ], where
], where 
Definition at line 419 of file eos.C.
References Lorene::Eos::calcule(), Lorene::Tensor::get_mp(), and Lorene::Eos::press_ent_p().
◆ press_ent_p()
|
virtual |
Computes the pressure from the log-enthalpy.
- Parameters
-
ent [input, unit:  ] log-enthalpy H defined by Eq. (4)
] log-enthalpy H defined by Eq. (4)par possible extra parameters of the EOS
- Returns
- pressure p [unit:
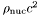 ], where
], where 
Implements Lorene::Eos.
Reimplemented in Lorene::Eos_poly_newt.
Definition at line 410 of file eos_poly.C.
References gam, kap, nbar_ent_p(), and Lorene::pow().
◆ sauve()
|
virtual |
Save in a file.
Reimplemented from Lorene::Eos.
Reimplemented in Lorene::Eos_poly_newt.
Definition at line 350 of file eos_poly.C.
References Lorene::fwrite_be(), gam, kap, m_0, mu_0, and Lorene::Eos::sauve().
◆ set_auxiliary()
|
protected |
Computes the auxiliary quantities gam1 , unsgam1 , gam1sgamkap from the values of gam and kap.
Definition at line 257 of file eos_poly.C.
References ent_0, gam, gam1, gam1sgamkap, kap, Lorene::log(), m_0, mu_0, rel_mu_0, and unsgam1.
◆ set_name()
|
inherited |
Friends And Related Function Documentation
◆ Eos::eos_from_file
|
friend |
The construction functions from a file.
Member Data Documentation
◆ ent_0
|
protected |
◆ gam
|
protected |
◆ gam1
◆ gam1sgamkap
◆ kap
|
protected |
◆ m_0
|
protected |
◆ mu_0
|
protected |
◆ name
◆ rel_mu_0
◆ unsgam1
The documentation for this class was generated from the following files:
