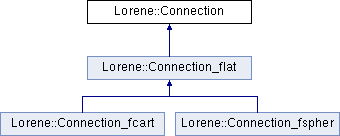
Class Connection. More...
#include <connection.h>
Public Member Functions | |
| Connection (const Tensor_sym &delta_i, const Metric_flat &flat_met_i) | |
| Standard constructor ab initio. More... | |
| Connection (const Metric &met, const Metric_flat &flat_met_i) | |
| Standard constructor for a connection associated with a metric. More... | |
| Connection (const Connection &) | |
| Copy constructor. More... | |
| virtual | ~Connection () |
| Destructor. More... | |
| void | operator= (const Connection &) |
Assignment to another Connection. More... | |
| void | update (const Tensor_sym &delta_i) |
| Update the connection when it is defined ab initio. More... | |
| void | update (const Metric &met) |
| Update the connection when it is associated with a metric. More... | |
| const Map & | get_mp () const |
| Returns the mapping. More... | |
| const Tensor_sym & | get_delta () const |
Returns the tensor  which defines the connection with respect to the flat one: which defines the connection with respect to the flat one:  is the difference between the connection coefficients is the difference between the connection coefficients 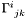 and the connection coefficients and the connection coefficients 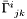 of the flat connection. More... of the flat connection. More... | |
| virtual Tensor * | p_derive_cov (const Tensor &tens) const |
Computes the covariant derivative 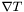 of a tensor of a tensor  (with respect to the current connection). More... (with respect to the current connection). More... | |
| virtual Tensor * | p_divergence (const Tensor &tens) const |
Computes the divergence of a tensor  (with respect to the current connection). More... (with respect to the current connection). More... | |
| virtual const Tensor & | ricci () const |
| Computes (if not up to date) and returns the Ricci tensor associated with the current connection. More... | |
Protected Member Functions | |
| Connection (const Map &, const Base_vect &) | |
| Constructor for derived classes. More... | |
| void | del_deriv () const |
| Deletes all the derived quantities. More... | |
| void | set_der_0x0 () const |
Sets to 0x0 all the pointers on derived quantities. More... | |
Protected Attributes | |
| const Map *const | mp |
| Reference mapping. More... | |
| const Base_vect *const | triad |
Triad 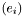 with respect to which the connection coefficients are defined. More... with respect to which the connection coefficients are defined. More... | |
| Tensor_sym | delta |
Tensor  which defines the connection with respect to the flat one: which defines the connection with respect to the flat one:  is the difference between the connection coefficients is the difference between the connection coefficients 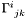 and the connection coefficients and the connection coefficients 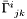 of the flat connection. More... of the flat connection. More... | |
| bool | assoc_metric |
| Indicates whether the connection is associated with a metric (in which case the Ricci tensor is symmetric, i.e. More... | |
| Tensor * | p_ricci |
| Pointer of the Ricci tensor associated with the connection. More... | |
Private Member Functions | |
| void | fait_delta (const Metric &) |
Computes the difference  between the connection coefficients and that a the flat connection in the case where the current connection is associated with a metric. More... between the connection coefficients and that a the flat connection in the case where the current connection is associated with a metric. More... | |
Private Attributes | |
| const Metric_flat * | flat_met |
Flat metric with respect to which  (member (member delta ) is defined. More... | |
Detailed Description
Class Connection.
()
This class deals only with torsion-free connections.
Note that we use the MTW convention for the indices of the connection coefficients with respect to a given triad 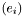 :
:
![\[ \Gamma^i_{\ jk} := \langle e^i, \nabla_{e_k} \, e_j \rangle \]](form_167.png)
Definition at line 113 of file connection.h.
Constructor & Destructor Documentation
◆ Connection() [1/4]
| Lorene::Connection::Connection | ( | const Tensor_sym & | delta_i, |
| const Metric_flat & | flat_met_i | ||
| ) |
Standard constructor ab initio.
- Parameters
-
delta_i tensor  which defines the connection with respect to the flat one:
which defines the connection with respect to the flat one:  is the difference between the connection coefficients
is the difference between the connection coefficients 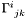 and the connection coefficients
and the connection coefficients 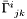 of the flat connection. The connection coefficients with respect to the triad
of the flat connection. The connection coefficients with respect to the triad 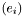 are defined according to the MTW convention:
are defined according to the MTW convention: ![\[ \Gamma^i_{\ jk} := \langle e^i, \nabla_{e_k} \, e_j \rangle \]](form_167.png)
 must be symmetric with respect to the indices j and k.
must be symmetric with respect to the indices j and k. flat_met_i flat metric with respect to which  is defined
is defined
Definition at line 132 of file connection.C.
References Lorene::Tensor::get_index_type(), Lorene::Tensor::get_valence(), set_der_0x0(), Lorene::Tensor_sym::sym_index1(), and Lorene::Tensor_sym::sym_index2().
◆ Connection() [2/4]
| Lorene::Connection::Connection | ( | const Metric & | met, |
| const Metric_flat & | flat_met_i | ||
| ) |
Standard constructor for a connection associated with a metric.
- Parameters
-
met Metric to which the connection will be associated flat_met_i flat metric to define the  representation of the connection
representation of the connection
Definition at line 153 of file connection.C.
References fait_delta(), and set_der_0x0().
◆ Connection() [3/4]
| Lorene::Connection::Connection | ( | const Connection & | conn_i | ) |
◆ Connection() [4/4]
Constructor for derived classes.
Definition at line 182 of file connection.C.
References set_der_0x0().
◆ ~Connection()
|
virtual |
Member Function Documentation
◆ del_deriv()
|
protected |
Deletes all the derived quantities.
Definition at line 208 of file connection.C.
References p_ricci, and set_der_0x0().
◆ fait_delta()
|
private |
Computes the difference  between the connection coefficients and that a the flat connection in the case where the current connection is associated with a metric.
between the connection coefficients and that a the flat connection in the case where the current connection is associated with a metric.
Definition at line 281 of file connection.C.
References Lorene::Metric::con(), Lorene::Metric::cov(), delta, Lorene::Tensor_sym::derive_cov(), flat_met, and Lorene::Tensor::set().
◆ get_delta()
|
inline |
Returns the tensor  which defines the connection with respect to the flat one:
which defines the connection with respect to the flat one:  is the difference between the connection coefficients
is the difference between the connection coefficients 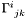 and the connection coefficients
and the connection coefficients 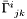 of the flat connection.
of the flat connection.
The connection coefficients with respect to the triad 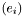 are defined according to the MTW convention:
are defined according to the MTW convention:
![\[ \Gamma^i_{\ jk} := \langle e^i, \nabla_{e_k} \, e_j \rangle \]](form_167.png)
Note that  is symmetric with respect to the indices j and k.
is symmetric with respect to the indices j and k.
- Returns
delta}(i,j,k) =
Definition at line 271 of file connection.h.
References delta.
◆ get_mp()
|
inline |
◆ operator=()
| void Lorene::Connection::operator= | ( | const Connection & | ci | ) |
Assignment to another Connection.
Definition at line 228 of file connection.C.
References del_deriv(), delta, flat_met, and triad.
◆ p_derive_cov()
Computes the covariant derivative 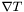 of a tensor
of a tensor  (with respect to the current connection).
(with respect to the current connection).
The extra index (with respect to the indices of  ) of
) of 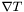 is chosen to be the last one. This convention agrees with that of MTW (see Eq. (10.17) of MTW). For instance, if
is chosen to be the last one. This convention agrees with that of MTW (see Eq. (10.17) of MTW). For instance, if  is a 1-form, whose components w.r.t. the triad
is a 1-form, whose components w.r.t. the triad 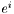 are
are 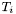 :
: 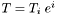 , then the covariant derivative of
, then the covariant derivative of  is the bilinear form
is the bilinear form 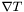 whose components
whose components 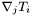 are such that
are such that
![\[ \nabla T = \nabla_j T_i \; e^i \otimes e^j \]](form_177.png)
- Parameters
-
tens tensor 
- Returns
- pointer on the covariant derivative
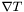 ; this pointer is polymorphe, i.e. it is a pointer on a
; this pointer is polymorphe, i.e. it is a pointer on a Vectorif the argument is aScalar, and on aTensorotherwise. NB: The corresponding memory is allocated by the methodp_derive_cov()and must be deallocated by the user afterwards.
Reimplemented in Lorene::Connection_fcart, Lorene::Connection_fspher, and Lorene::Connection_flat.
Definition at line 310 of file connection.C.
References Lorene::Scalar::dec_dzpuis(), delta, Lorene::Tensor::derive_cov(), flat_met, Lorene::Tensor::get_index_type(), Lorene::Tensor::get_n_comp(), Lorene::Tensor::get_triad(), Lorene::Tensor::get_valence(), Lorene::Tensor::indices(), mp, Lorene::Itbl::set(), Lorene::Tensor::set(), Lorene::Tensor_sym::sym_index1(), Lorene::Tensor_sym::sym_index2(), and triad.
◆ p_divergence()
Computes the divergence of a tensor  (with respect to the current connection).
(with respect to the current connection).
The divergence is taken with respect of the last index of  which thus must be contravariant. For instance if
which thus must be contravariant. For instance if  is a twice contravariant tensor, whose components w.r.t. the triad
is a twice contravariant tensor, whose components w.r.t. the triad 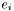 are
are 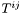 :
: 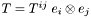 , the divergence of
, the divergence of  is the vector
is the vector
![\[ {\rm div}\, T = \nabla_k T^{ik} \; e_i \]](form_181.png)
where 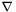 denotes the current connection.
denotes the current connection.
- Parameters
-
tens tensor 
- Returns
- pointer on the divergence of
 ; this pointer is polymorphe, i.e. its is a pointer on a
; this pointer is polymorphe, i.e. its is a pointer on a Scalarif is a
is a Vector, on aVectorif is a tensor of valence 2, and on a
is a tensor of valence 2, and on a Tensorotherwise. NB: The corresponding memory is allocated by the methodp_divergence()and must be deallocated by the user afterwards.
Reimplemented in Lorene::Connection_fcart, Lorene::Connection_fspher, and Lorene::Connection_flat.
Definition at line 466 of file connection.C.
References Lorene::Scalar::dec_dzpuis(), delta, Lorene::Tensor::divergence(), flat_met, Lorene::Tensor::get_index_type(), Lorene::Tensor::get_n_comp(), Lorene::Tensor::get_triad(), Lorene::Tensor::get_valence(), Lorene::Tensor::indices(), mp, Lorene::Itbl::set(), Lorene::Tensor_sym::sym_index1(), Lorene::Tensor_sym::sym_index2(), Lorene::Tensor::trace(), and triad.
◆ ricci()
|
virtual |
Computes (if not up to date) and returns the Ricci tensor associated with the current connection.
Reimplemented in Lorene::Connection_flat.
Definition at line 665 of file connection.C.
References assoc_metric, Lorene::Scalar::dec_dzpuis(), delta, Lorene::Tensor_sym::derive_cov(), flat_met, mp, p_ricci, Lorene::Tensor::set(), Lorene::Scalar::set_etat_zero(), and triad.
◆ set_der_0x0()
|
protected |
Sets to 0x0 all the pointers on derived quantities.
Definition at line 216 of file connection.C.
References p_ricci.
◆ update() [1/2]
| void Lorene::Connection::update | ( | const Tensor_sym & | delta_i | ) |
Update the connection when it is defined ab initio.
- Parameters
-
delta_i tensor  which defines the connection with respect to the flat one:
which defines the connection with respect to the flat one:  is the difference between the connection coefficients
is the difference between the connection coefficients 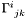 and the connection coefficients
and the connection coefficients 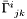 of the flat connection.
of the flat connection.  must be symmetric with respect to the indices j and k.
must be symmetric with respect to the indices j and k.
Definition at line 238 of file connection.C.
References assoc_metric, del_deriv(), delta, flat_met, Lorene::Tensor::get_index_type(), Lorene::Tensor::get_valence(), Lorene::Tensor_sym::sym_index1(), and Lorene::Tensor_sym::sym_index2().
◆ update() [2/2]
| void Lorene::Connection::update | ( | const Metric & | met | ) |
Update the connection when it is associated with a metric.
- Parameters
-
met Metric to which the connection is associated
Definition at line 258 of file connection.C.
References assoc_metric, del_deriv(), fait_delta(), and flat_met.
Member Data Documentation
◆ assoc_metric
|
protected |
Indicates whether the connection is associated with a metric (in which case the Ricci tensor is symmetric, i.e.
the actual type of p_ricci is a Sym_tensor )
Definition at line 147 of file connection.h.
◆ delta
|
protected |
Tensor  which defines the connection with respect to the flat one:
which defines the connection with respect to the flat one:  is the difference between the connection coefficients
is the difference between the connection coefficients 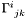 and the connection coefficients
and the connection coefficients 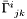 of the flat connection.
of the flat connection.
The connection coefficients with respect to the triad 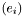 are defined according to the MTW convention:
are defined according to the MTW convention:
![\[ \Gamma^i_{\ jk} := \langle e^i, \nabla_{e_k} \, e_j \rangle \]](form_167.png)
Note that  is symmetric with respect to the indices j and k.
is symmetric with respect to the indices j and k.
Definition at line 141 of file connection.h.
◆ flat_met
|
private |
Flat metric with respect to which  (member
(member delta ) is defined.
Definition at line 156 of file connection.h.
◆ mp
|
protected |
Reference mapping.
Definition at line 119 of file connection.h.
◆ p_ricci
|
mutableprotected |
Pointer of the Ricci tensor associated with the connection.
Definition at line 164 of file connection.h.
◆ triad
|
protected |
Triad 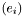 with respect to which the connection coefficients are defined.
with respect to which the connection coefficients are defined.
Definition at line 124 of file connection.h.
The documentation for this class was generated from the following files:
