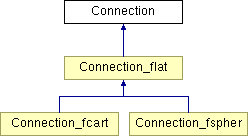
Connection Class Reference
[Tensorial fields]
Class Connection. More...
#include <connection.h>
Public Member Functions | |
| Connection (const Tensor_sym &delta_i, const Metric_flat &flat_met_i) | |
| Standard constructor ab initio. | |
| Connection (const Metric &met, const Metric_flat &flat_met_i) | |
| Standard constructor for a connection associated with a metric. | |
| Connection (const Connection &) | |
| Copy constructor. | |
| virtual | ~Connection () |
| Destructor. | |
| void | operator= (const Connection &) |
Assignment to another Connection. | |
| void | update (const Tensor_sym &delta_i) |
| Update the connection when it is defined ab initio. | |
| void | update (const Metric &met) |
| Update the connection when it is associated with a metric. | |
| const Map & | get_mp () const |
| Returns the mapping. | |
| const Tensor_sym & | get_delta () const |
Returns the tensor  which defines the connection with respect to the flat one: which defines the connection with respect to the flat one:  is the difference between the connection coefficients is the difference between the connection coefficients 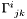 and the connection coefficients and the connection coefficients 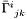 of the flat connection. of the flat connection. | |
| virtual Tensor * | p_derive_cov (const Tensor &tens) const |
Computes the covariant derivative 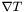 of a tensor of a tensor  (with respect to the current connection). (with respect to the current connection). | |
| virtual Tensor * | p_divergence (const Tensor &tens) const |
Computes the divergence of a tensor  (with respect to the current connection). (with respect to the current connection). | |
| virtual const Tensor & | ricci () const |
| Computes (if not up to date) and returns the Ricci tensor associated with the current connection. | |
Protected Member Functions | |
| Connection (const Map &, const Base_vect &) | |
| Constructor for derived classes. | |
| void | del_deriv () const |
| Deletes all the derived quantities. | |
| void | set_der_0x0 () const |
Sets to 0x0 all the pointers on derived quantities. | |
Protected Attributes | |
| const Map *const | mp |
| Reference mapping. | |
| const Base_vect *const | triad |
Triad 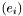 with respect to which the connection coefficients are defined. with respect to which the connection coefficients are defined. | |
| Tensor_sym | delta |
Tensor  which defines the connection with respect to the flat one: which defines the connection with respect to the flat one:  is the difference between the connection coefficients is the difference between the connection coefficients 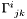 and the connection coefficients and the connection coefficients 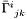 of the flat connection. of the flat connection. | |
| bool | assoc_metric |
| Indicates whether the connection is associated with a metric (in which case the Ricci tensor is symmetric, i.e. | |
| Tensor * | p_ricci |
| Pointer of the Ricci tensor associated with the connection. | |
Private Member Functions | |
| void | fait_delta (const Metric &) |
Computes the difference  between the connection coefficients and that a the flat connection in the case where the current connection is associated with a metric. between the connection coefficients and that a the flat connection in the case where the current connection is associated with a metric. | |
Private Attributes | |
| const Metric_flat * | flat_met |
Flat metric with respect to which  (member (member delta ) is defined. | |
Detailed Description
Class Connection.
()
This class deals only with torsion-free connections.
Note that we use the MTW convention for the indices of the connection coefficients with respect to a given triad 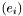 :
:
![\[ \Gamma^i_{\ jk} := \langle e^i, \nabla_{e_k} \, e_j \rangle \]](form_167.png)
Definition at line 109 of file connection.h.
Constructor & Destructor Documentation
| Connection::Connection | ( | const Tensor_sym & | delta_i, | |
| const Metric_flat & | flat_met_i | |||
| ) |
Standard constructor ab initio.
- Parameters:
-
delta_i tensor  which defines the connection with respect to the flat one:
which defines the connection with respect to the flat one:  is the difference between the connection coefficients
is the difference between the connection coefficients 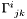 and the connection coefficients
and the connection coefficients 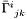 of the flat connection. The connection coefficients with respect to the triad
of the flat connection. The connection coefficients with respect to the triad 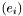 are defined according to the MTW convention:
are defined according to the MTW convention:
![\[ \Gamma^i_{\ jk} := \langle e^i, \nabla_{e_k} \, e_j \rangle \]](form_167.png)
 must be symmetric with respect to the indices j and k.
must be symmetric with respect to the indices j and k. flat_met_i flat metric with respect to which  is defined
is defined
Definition at line 125 of file connection.C.
References Tensor::get_index_type(), Tensor::get_valence(), set_der_0x0(), Tensor_sym::sym_index1(), and Tensor_sym::sym_index2().
| Connection::Connection | ( | const Metric & | met, | |
| const Metric_flat & | flat_met_i | |||
| ) |
Standard constructor for a connection associated with a metric.
- Parameters:
-
met Metric to which the connection will be associated flat_met_i flat metric to define the  representation of the connection
representation of the connection
Definition at line 146 of file connection.C.
References fait_delta(), and set_der_0x0().
| Connection::Connection | ( | const Connection & | conn_i | ) |
Constructor for derived classes.
Definition at line 175 of file connection.C.
References set_der_0x0().
| Connection::~Connection | ( | ) | [virtual] |
Member Function Documentation
| void Connection::del_deriv | ( | ) | const [protected] |
Deletes all the derived quantities.
Definition at line 201 of file connection.C.
References p_ricci, and set_der_0x0().
| void Connection::fait_delta | ( | const Metric & | gam | ) | [private] |
Computes the difference  between the connection coefficients and that a the flat connection in the case where the current connection is associated with a metric.
between the connection coefficients and that a the flat connection in the case where the current connection is associated with a metric.
Definition at line 274 of file connection.C.
References Metric::con(), Metric::cov(), delta, Tensor_sym::derive_cov(), flat_met, and Tensor::set().
| const Tensor_sym& Connection::get_delta | ( | ) | const [inline] |
Returns the tensor  which defines the connection with respect to the flat one:
which defines the connection with respect to the flat one:  is the difference between the connection coefficients
is the difference between the connection coefficients 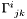 and the connection coefficients
and the connection coefficients 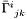 of the flat connection.
of the flat connection.
The connection coefficients with respect to the triad 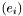 are defined according to the MTW convention:
are defined according to the MTW convention:
![\[ \Gamma^i_{\ jk} := \langle e^i, \nabla_{e_k} \, e_j \rangle \]](form_167.png)
Note that  is symmetric with respect to the indices j and k.
is symmetric with respect to the indices j and k.
- Returns:
delta}(i,j,k) =
Definition at line 267 of file connection.h.
References delta.
| const Map& Connection::get_mp | ( | ) | const [inline] |
| void Connection::operator= | ( | const Connection & | ci | ) |
Assignment to another Connection.
Reimplemented in Connection_flat, Connection_fspher, and Connection_fcart.
Definition at line 221 of file connection.C.
References del_deriv(), delta, flat_met, and triad.
Computes the covariant derivative 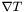 of a tensor
of a tensor  (with respect to the current connection).
(with respect to the current connection).
The extra index (with respect to the indices of  ) of
) of 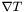 is chosen to be the last one. This convention agrees with that of MTW (see Eq. (10.17) of MTW). For instance, if
is chosen to be the last one. This convention agrees with that of MTW (see Eq. (10.17) of MTW). For instance, if  is a 1-form, whose components w.r.t. the triad
is a 1-form, whose components w.r.t. the triad 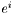 are
are 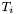 :
: 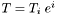 , then the covariant derivative of
, then the covariant derivative of  is the bilinear form
is the bilinear form 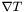 whose components
whose components 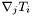 are such that
are such that
![\[ \nabla T = \nabla_j T_i \; e^i \otimes e^j \]](form_177.png)
- Parameters:
-
tens tensor 
- Returns:
- pointer on the covariant derivative
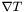 ; this pointer is polymorphe, i.e. it is a pointer on a
; this pointer is polymorphe, i.e. it is a pointer on a Vectorif the argument is aScalar, and on aTensorotherwise. NB: The corresponding memory is allocated by the methodp_derive_cov()and must be deallocated by the user afterwards.
Reimplemented in Connection_flat, Connection_fspher, and Connection_fcart.
Definition at line 303 of file connection.C.
References Scalar::dec_dzpuis(), delta, Tensor::derive_cov(), flat_met, Tensor::get_index_type(), Tensor::get_n_comp(), Tensor::get_triad(), Tensor::get_valence(), Tensor::indices(), mp, Tensor::set(), Itbl::set(), Tensor_sym::sym_index1(), Tensor_sym::sym_index2(), and triad.
Computes the divergence of a tensor  (with respect to the current connection).
(with respect to the current connection).
The divergence is taken with respect of the last index of  which thus must be contravariant. For instance if
which thus must be contravariant. For instance if  is a twice contravariant tensor, whose components w.r.t. the triad
is a twice contravariant tensor, whose components w.r.t. the triad 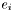 are
are 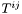 :
: 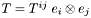 , the divergence of
, the divergence of  is the vector
is the vector
![\[ {\rm div}\, T = \nabla_k T^{ik} \; e_i \]](form_181.png)
where 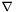 denotes the current connection.
denotes the current connection.
- Parameters:
-
tens tensor 
- Returns:
- pointer on the divergence of
 ; this pointer is polymorphe, i.e. its is a pointer on a
; this pointer is polymorphe, i.e. its is a pointer on a Scalarif is a
is a Vector, on aVectorif is a tensor of valence 2, and on a
is a tensor of valence 2, and on a Tensorotherwise. NB: The corresponding memory is allocated by the methodp_divergence()and must be deallocated by the user afterwards.
Reimplemented in Connection_flat, Connection_fspher, and Connection_fcart.
Definition at line 459 of file connection.C.
References Scalar::dec_dzpuis(), delta, Tensor::divergence(), flat_met, Tensor::get_index_type(), Tensor::get_n_comp(), Tensor::get_triad(), Tensor::get_valence(), Tensor::indices(), mp, Itbl::set(), Tensor_sym::sym_index1(), Tensor_sym::sym_index2(), Tensor::trace(), and triad.
| const Tensor & Connection::ricci | ( | ) | const [virtual] |
Computes (if not up to date) and returns the Ricci tensor associated with the current connection.
Reimplemented in Connection_flat.
Definition at line 658 of file connection.C.
References assoc_metric, Scalar::dec_dzpuis(), delta, Tensor_sym::derive_cov(), flat_met, mp, p_ricci, Tensor::set(), Scalar::set_etat_zero(), and triad.
| void Connection::set_der_0x0 | ( | ) | const [protected] |
Sets to 0x0 all the pointers on derived quantities.
Definition at line 209 of file connection.C.
References p_ricci.
| void Connection::update | ( | const Metric & | met | ) |
Update the connection when it is associated with a metric.
- Parameters:
-
met Metric to which the connection is associated
Definition at line 251 of file connection.C.
References assoc_metric, del_deriv(), fait_delta(), and flat_met.
| void Connection::update | ( | const Tensor_sym & | delta_i | ) |
Update the connection when it is defined ab initio.
- Parameters:
-
delta_i tensor  which defines the connection with respect to the flat one:
which defines the connection with respect to the flat one:  is the difference between the connection coefficients
is the difference between the connection coefficients 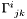 and the connection coefficients
and the connection coefficients 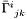 of the flat connection.
of the flat connection.  must be symmetric with respect to the indices j and k.
must be symmetric with respect to the indices j and k.
Definition at line 231 of file connection.C.
References assoc_metric, del_deriv(), delta, flat_met, Tensor::get_index_type(), Tensor::get_valence(), Tensor_sym::sym_index1(), and Tensor_sym::sym_index2().
Member Data Documentation
bool Connection::assoc_metric [protected] |
Indicates whether the connection is associated with a metric (in which case the Ricci tensor is symmetric, i.e.
the actual type of p_ricci is a Sym_tensor )
Definition at line 143 of file connection.h.
Tensor_sym Connection::delta [protected] |
Tensor  which defines the connection with respect to the flat one:
which defines the connection with respect to the flat one:  is the difference between the connection coefficients
is the difference between the connection coefficients 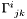 and the connection coefficients
and the connection coefficients 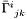 of the flat connection.
of the flat connection.
The connection coefficients with respect to the triad 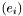 are defined according to the MTW convention:
are defined according to the MTW convention:
![\[ \Gamma^i_{\ jk} := \langle e^i, \nabla_{e_k} \, e_j \rangle \]](form_167.png)
Note that  is symmetric with respect to the indices j and k.
is symmetric with respect to the indices j and k.
Definition at line 137 of file connection.h.
const Metric_flat* Connection::flat_met [private] |
Flat metric with respect to which  (member
(member delta ) is defined.
Definition at line 152 of file connection.h.
const Map* const Connection::mp [protected] |
Reference mapping.
Definition at line 115 of file connection.h.
Tensor* Connection::p_ricci [mutable, protected] |
Pointer of the Ricci tensor associated with the connection.
Definition at line 160 of file connection.h.
const Base_vect* const Connection::triad [protected] |
Triad 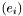 with respect to which the connection coefficients are defined.
with respect to which the connection coefficients are defined.
Definition at line 120 of file connection.h.
The documentation for this class was generated from the following files:
 1.6.1
1.6.1