Connection_fcart Class Reference
[Tensorial fields]
Class Connection_fcart. More...
#include <connection.h>
Public Member Functions | |
| Connection_fcart (const Map &, const Base_vect_cart &) | |
| Contructor from a Cartesian flat-metric-orthonormal basis. | |
| Connection_fcart (const Connection_fcart &) | |
| Copy constructor. | |
| virtual | ~Connection_fcart () |
| destructor | |
| void | operator= (const Connection_fcart &) |
Assignment to another Connection_fcart. | |
| virtual Tensor * | p_derive_cov (const Tensor &tens) const |
Computes the covariant derivative 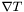 of a tensor of a tensor  (with respect to the current connection). (with respect to the current connection). | |
| virtual Tensor * | p_divergence (const Tensor &tens) const |
Computes the divergence of a tensor  (with respect to the current connection). (with respect to the current connection). | |
| virtual const Tensor & | ricci () const |
| Computes (if not up to date) and returns the Ricci tensor associated with the current connection. | |
| void | update (const Tensor_sym &delta_i) |
| Update the connection when it is defined ab initio. | |
| void | update (const Metric &met) |
| Update the connection when it is associated with a metric. | |
| const Map & | get_mp () const |
| Returns the mapping. | |
| const Tensor_sym & | get_delta () const |
Returns the tensor  which defines the connection with respect to the flat one: which defines the connection with respect to the flat one:  is the difference between the connection coefficients is the difference between the connection coefficients 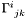 and the connection coefficients and the connection coefficients 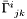 of the flat connection. of the flat connection. | |
Protected Member Functions | |
| void | del_deriv () const |
| Deletes all the derived quantities. | |
| void | set_der_0x0 () const |
Sets to 0x0 all the pointers on derived quantities. | |
Protected Attributes | |
| const Map *const | mp |
| Reference mapping. | |
| const Base_vect *const | triad |
Triad 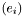 with respect to which the connection coefficients are defined. with respect to which the connection coefficients are defined. | |
| Tensor_sym | delta |
Tensor  which defines the connection with respect to the flat one: which defines the connection with respect to the flat one:  is the difference between the connection coefficients is the difference between the connection coefficients 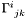 and the connection coefficients and the connection coefficients 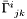 of the flat connection. of the flat connection. | |
| bool | assoc_metric |
| Indicates whether the connection is associated with a metric (in which case the Ricci tensor is symmetric, i.e. | |
| Tensor * | p_ricci |
| Pointer of the Ricci tensor associated with the connection. | |
Detailed Description
Class Connection_fcart.
()
Class for connections associated with a flat metric and given onto an orthonormal Cartesian triad.
Definition at line 542 of file connection.h.
Constructor & Destructor Documentation
| Connection_fcart::Connection_fcart | ( | const Map & | mpi, | |
| const Base_vect_cart & | bi | |||
| ) |
Contructor from a Cartesian flat-metric-orthonormal basis.
Definition at line 105 of file connection_fcart.C.
| Connection_fcart::Connection_fcart | ( | const Connection_fcart & | ci | ) |
Copy constructor.
Definition at line 111 of file connection_fcart.C.
| Connection_fcart::~Connection_fcart | ( | ) | [virtual] |
destructor
Definition at line 122 of file connection_fcart.C.
Member Function Documentation
| void Connection::del_deriv | ( | ) | const [protected, inherited] |
Deletes all the derived quantities.
Definition at line 201 of file connection.C.
References Connection::p_ricci, and Connection::set_der_0x0().
| const Tensor_sym& Connection::get_delta | ( | ) | const [inline, inherited] |
Returns the tensor  which defines the connection with respect to the flat one:
which defines the connection with respect to the flat one:  is the difference between the connection coefficients
is the difference between the connection coefficients 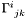 and the connection coefficients
and the connection coefficients 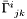 of the flat connection.
of the flat connection.
The connection coefficients with respect to the triad 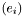 are defined according to the MTW convention:
are defined according to the MTW convention:
![\[ \Gamma^i_{\ jk} := \langle e^i, \nabla_{e_k} \, e_j \rangle \]](form_167.png)
Note that  is symmetric with respect to the indices j and k.
is symmetric with respect to the indices j and k.
- Returns:
delta}(i,j,k) =
Definition at line 267 of file connection.h.
References Connection::delta.
| const Map& Connection::get_mp | ( | ) | const [inline, inherited] |
| void Connection_fcart::operator= | ( | const Connection_fcart & | ) |
Assignment to another Connection_fcart.
Reimplemented from Connection_flat.
Definition at line 132 of file connection_fcart.C.
Computes the covariant derivative 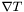 of a tensor
of a tensor  (with respect to the current connection).
(with respect to the current connection).
The extra index (with respect to the indices of  ) of
) of 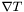 is chosen to be the last one. This convention agrees with that of MTW (see Eq. (10.17) of MTW). For instance, if
is chosen to be the last one. This convention agrees with that of MTW (see Eq. (10.17) of MTW). For instance, if  is a 1-form, whose components w.r.t. the triad
is a 1-form, whose components w.r.t. the triad 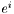 are
are 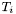 :
: 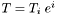 , then the covariant derivative of
, then the covariant derivative of  is the bilinear form
is the bilinear form 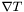 whose components
whose components 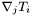 are such that
are such that
![\[ \nabla T = \nabla_j T_i \; e^i \otimes e^j \]](form_177.png)
- Parameters:
-
tens tensor 
- Returns:
- pointer on the covariant derivative
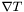 ; this pointer is polymorphe, i.e. it is a pointer on a
; this pointer is polymorphe, i.e. it is a pointer on a Vectorif the argument is aScalar, and on aTensorotherwise. NB: The corresponding memory is allocated by the methodp_derive_cov()and must be deallocated by the user afterwards.
Implements Connection_flat.
Definition at line 148 of file connection_fcart.C.
References Tensor::get_index_type(), Tensor::get_n_comp(), Tensor::get_triad(), Tensor::get_valence(), Tensor::indices(), Connection::mp, Tensor::set(), Itbl::set(), Tensor_sym::sym_index1(), Tensor_sym::sym_index2(), and Connection::triad.
Computes the divergence of a tensor  (with respect to the current connection).
(with respect to the current connection).
The divergence is taken with respect of the last index of  which thus must be contravariant. For instance if
which thus must be contravariant. For instance if  is a twice contravariant tensor, whose components w.r.t. the triad
is a twice contravariant tensor, whose components w.r.t. the triad 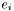 are
are 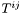 :
: 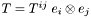 , the divergence of
, the divergence of  is the vector
is the vector
![\[ {\rm div} T = \nabla_k T^{ik} \; e_i \]](form_183.png)
where 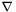 denotes the current connection.
denotes the current connection.
- Parameters:
-
tens tensor 
- Returns:
- pointer on the divergence of
 ; this pointer is polymorphe, i.e. its is a pointer on a
; this pointer is polymorphe, i.e. its is a pointer on a Scalarif is a
is a Vector, on aVectorif is a tensor of valence 2, and on a
is a tensor of valence 2, and on a Tensorotherwise. NB: The corresponding memory is allocated by the methodp_divergence()and must be deallocated by the user afterwards.
Implements Connection_flat.
Definition at line 234 of file connection_fcart.C.
References Tensor::get_index_type(), Tensor::get_triad(), Tensor::get_valence(), Connection::mp, Itbl::set(), Scalar::set_etat_zero(), Tensor_sym::sym_index1(), Tensor_sym::sym_index2(), and Connection::triad.
| const Tensor & Connection_flat::ricci | ( | ) | const [virtual, inherited] |
Computes (if not up to date) and returns the Ricci tensor associated with the current connection.
Reimplemented from Connection.
Definition at line 117 of file connection_flat.C.
References Connection::mp, Connection::p_ricci, Tensor::set_etat_zero(), and Connection::triad.
| void Connection::set_der_0x0 | ( | ) | const [protected, inherited] |
Sets to 0x0 all the pointers on derived quantities.
Definition at line 209 of file connection.C.
References Connection::p_ricci.
| void Connection::update | ( | const Metric & | met | ) | [inherited] |
Update the connection when it is associated with a metric.
- Parameters:
-
met Metric to which the connection is associated
Definition at line 251 of file connection.C.
References Connection::assoc_metric, Connection::del_deriv(), Connection::fait_delta(), and Connection::flat_met.
| void Connection::update | ( | const Tensor_sym & | delta_i | ) | [inherited] |
Update the connection when it is defined ab initio.
- Parameters:
-
delta_i tensor  which defines the connection with respect to the flat one:
which defines the connection with respect to the flat one:  is the difference between the connection coefficients
is the difference between the connection coefficients 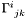 and the connection coefficients
and the connection coefficients 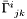 of the flat connection.
of the flat connection.  must be symmetric with respect to the indices j and k.
must be symmetric with respect to the indices j and k.
Definition at line 231 of file connection.C.
References Connection::assoc_metric, Connection::del_deriv(), Connection::delta, Connection::flat_met, Tensor::get_index_type(), Tensor::get_valence(), Tensor_sym::sym_index1(), and Tensor_sym::sym_index2().
Member Data Documentation
bool Connection::assoc_metric [protected, inherited] |
Indicates whether the connection is associated with a metric (in which case the Ricci tensor is symmetric, i.e.
the actual type of p_ricci is a Sym_tensor )
Definition at line 143 of file connection.h.
Tensor_sym Connection::delta [protected, inherited] |
Tensor  which defines the connection with respect to the flat one:
which defines the connection with respect to the flat one:  is the difference between the connection coefficients
is the difference between the connection coefficients 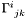 and the connection coefficients
and the connection coefficients 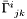 of the flat connection.
of the flat connection.
The connection coefficients with respect to the triad 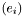 are defined according to the MTW convention:
are defined according to the MTW convention:
![\[ \Gamma^i_{\ jk} := \langle e^i, \nabla_{e_k} \, e_j \rangle \]](form_167.png)
Note that  is symmetric with respect to the indices j and k.
is symmetric with respect to the indices j and k.
Definition at line 137 of file connection.h.
const Map* const Connection::mp [protected, inherited] |
Reference mapping.
Definition at line 115 of file connection.h.
Tensor* Connection::p_ricci [mutable, protected, inherited] |
Pointer of the Ricci tensor associated with the connection.
Definition at line 160 of file connection.h.
const Base_vect* const Connection::triad [protected, inherited] |
Triad 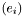 with respect to which the connection coefficients are defined.
with respect to which the connection coefficients are defined.
Definition at line 120 of file connection.h.
The documentation for this class was generated from the following files:
 1.6.1
1.6.1