() More...
Functions | |
| Tenseur | Lorene::operator* (const Tenseur &, const Tenseur &) |
| Tensorial product. More... | |
| Tenseur | Lorene::operator% (const Tenseur &, const Tenseur &) |
| Tensorial product with desaliasing. More... | |
| Tenseur | Lorene::contract (const Tenseur &, int id1, int id2) |
Self contraction of two indices of a Tenseur . More... | |
| Tenseur | Lorene::contract (const Tenseur &, int id1, const Tenseur &, int id2) |
Contraction of two Tenseur . More... | |
| Tenseur | Lorene::flat_scalar_prod (const Tenseur &t1, const Tenseur &t2) |
Scalar product of two Tenseur when the metric is 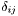 : performs the contraction of the last index of : performs the contraction of the last index of t1 with the first one of t2 , irrespective of the type of these indices. More... | |
| Tenseur | Lorene::flat_scalar_prod_desal (const Tenseur &t1, const Tenseur &t2) |
Same as flat_scalar_prod but with desaliasing. More... | |
| Tenseur | Lorene::manipule (const Tenseur &, const Metrique &, int idx) |
Raise or lower the index idx depending on its type, using the given Metrique . More... | |
| Tenseur | Lorene::manipule (const Tenseur &, const Metrique &) |
Raise or lower all the indices, depending on their type, using the given Metrique . More... | |
| Tenseur | Lorene::skxk (const Tenseur &) |
Contraction of the last index of (*this) with 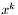 or or 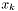 , depending on the type of S . More... , depending on the type of S . More... | |
| Tenseur | Lorene::lie_derive (const Tenseur &t, const Tenseur &x, const Metrique *=0x0) |
Lie Derivative of t with respect to x . More... | |
| Tenseur | Lorene::sans_trace (const Tenseur &tens, const Metrique &metre) |
Computes the traceless part of a Tenseur of valence 2. More... | |
Detailed Description
()
Function Documentation
◆ contract() [1/2]
Self contraction of two indices of a Tenseur .
The two indices must be of different type, i.e. covariant and contravariant, or contravariant and covariant.
- Parameters
-
id1 [input] number of the first index for the contraction; id1must be strictly lower than the valence of the tensor and obeys the following convention:id1= 0 : first indexid1= 1 : second index- and so on...
id2 [input] number of the second index for the contraction; id2must be strictly lower than the valence of the tensor and obeys the following convention:id2= 0 : first indexid2= 1 : second index- and so on...
Definition at line 282 of file tenseur_operateur.C.
References Lorene::Tenseur::etat.
◆ contract() [2/2]
Contraction of two Tenseur .
The two indices must be of different type, i.e. covariant and contravariant, or contravariant and covariant.
- Parameters
-
id1 [input] number of the index of contraction for the first Tenseur;id1must be strictly lower than the valence of the tensor and obeys the following convention:id1= 0 : first indexid1= 1 : second index- and so on...
id2 [input] number of index of contraction for the second one; id2must be strictly lower than the valence of the tensor and obeys the following convention:id2= 0 : first indexid2= 1 : second index- and so on...
Definition at line 351 of file tenseur_operateur.C.
References Lorene::Tenseur::etat.
◆ flat_scalar_prod()
Scalar product of two Tenseur when the metric is 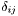 : performs the contraction of the last index of
: performs the contraction of the last index of t1 with the first one of t2 , irrespective of the type of these indices.
Definition at line 656 of file tenseur_operateur.C.
References Lorene::Tenseur::etat.
◆ flat_scalar_prod_desal()
Same as flat_scalar_prod but with desaliasing.
Definition at line 738 of file tenseur_operateur.C.
References Lorene::Tenseur::etat.
◆ lie_derive()
Lie Derivative of t with respect to x .
If no other argument is given, it uses partial derivatives with respect to cartesian coordinates to calculate the result (this is the default). Otherwise, it uses the covariant derivative associated to the metric given as last argument.
Definition at line 819 of file tenseur_operateur.C.
References Lorene::Tenseur::get_etat().
◆ manipule() [1/2]
Raise or lower the index idx depending on its type, using the given Metrique .
Definition at line 512 of file tenseur_operateur.C.
References Lorene::Tenseur::etat.
◆ manipule() [2/2]
Raise or lower all the indices, depending on their type, using the given Metrique .
Definition at line 565 of file tenseur_operateur.C.
References Lorene::manipule(), and Lorene::Tenseur::valence.
◆ operator%()
Tensorial product with desaliasing.
Definition at line 202 of file tenseur_operateur.C.
References Lorene::Tenseur::etat.
◆ operator*()
Tensorial product.
Definition at line 122 of file tenseur_operateur.C.
References Lorene::Tenseur::etat.
◆ sans_trace()
Computes the traceless part of a Tenseur of valence 2.
- Parameters
-
tens [input] the Tenseurof valence 2metre [input] the metric used to raise or lower the indices
- Returns
- The traceless part of the input
Tenseur
Definition at line 900 of file tenseur_operateur.C.
References Lorene::Tenseur::get_etat().
◆ skxk()
Contraction of the last index of (*this) with 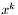 or
or 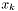 , depending on the type of S .
, depending on the type of S .
The calculation is performed to avoid singularities in the external zone. This is done only for a flat metric.
Definition at line 583 of file tenseur_operateur.C.
References Lorene::Tenseur::etat, and Lorene::Tenseur::valence.
