Polytropic equation of state (relativistic case) for use in dynamical code. More...
#include <dyneos.h>
Public Member Functions | |
| Dyn_eos_poly (double gamma, double kappa) | |
Standard constructor (sets both m_0 and mu_0 to 1). More... | |
| Dyn_eos_poly (double gamma, double kappa, double mass) | |
Standard constructor with individual particle mass (sets mu_0 to 1). More... | |
| Dyn_eos_poly (double gamma, double kappa, double mass, double mu_zero) | |
| Standard constructor with individual particle mass and zero-pressure chemical potential. More... | |
| Dyn_eos_poly (const Dyn_eos_poly &) | |
| Copy constructor. More... | |
| virtual | ~Dyn_eos_poly () |
| Destructor. More... | |
| void | operator= (const Dyn_eos_poly &) |
Assignment to another Dyn_eos_poly. More... | |
| virtual bool | operator== (const Dyn_eos &) const |
| Comparison operator (egality) More... | |
| virtual bool | operator!= (const Dyn_eos &) const |
| Comparison operator (difference) More... | |
| virtual int | identify () const |
Returns a number to identify the sub-classe of Dyn_eos the object belongs to. More... | |
| double | get_gam () const |
Returns the adiabatic index  (cf. Eq. (3)) More... (cf. Eq. (3)) More... | |
| double | get_kap () const |
Returns the pressure coefficient 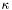 (cf. More... (cf. More... | |
| double | get_m_0 () const |
Return the individual particule mass 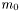 (cf. More... (cf. More... | |
| double | get_mu_0 () const |
Return the relativistic chemical potential at zero pressure [unit: 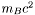 , with , with  ]. More... ]. More... | |
| virtual void | sauve (FILE *) const |
| Save in a file. More... | |
| virtual double | ent_nbar_p (double nbar, const Param *par=0x0) const |
| Computes the log-enthalpy from the baryon density and extra parameters (virtual function implemented in the derived classes). More... | |
| virtual double | ener_nbar_p (double nbar, const Param *par=0x0) const |
| Computes the total energy density from the baryon density and extra parameters (virtual function implemented in the derived classes). More... | |
| virtual double | press_nbar_p (double nbar, const Param *par=0x0) const |
| Computes the pressure from the baryon density and extra parameters (virtual function implemented in the derived classes). More... | |
| virtual double | csound_square_nbar_p (double nbar, const Param *par=0x0) const |
Computes the sound speed squared 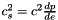 from the baryon density with extra parameters. More... from the baryon density with extra parameters. More... | |
| const string & | get_name () const |
| Returns the EOS name. More... | |
| void | set_name (const string &) |
| Sets the EOS name. More... | |
| Scalar | ent_nbar (const Scalar &nbar, int nzet, int l_min=0, Param *par=0x0) const |
| Computes the log-enthalpy field from the baryon density field and extra parameters. More... | |
| Scalar | ener_nbar (const Scalar &nbar, int nzet, int l_min=0, Param *par=0x0) const |
| Computes the total energy density from the baryon density and extra parameters. More... | |
| Scalar | press_nbar (const Scalar &nbar, int nzet, int l_min=0, Param *par=0x0) const |
| Computes the pressure from the baryon density and extra parameters. More... | |
| Scalar | csound_square_nbar (const Scalar &nbar, int nzet, int l_min=0, Param *par=0x0) const |
Computes the sound speed squared 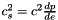 from the baryon density with extra parameters. More... from the baryon density with extra parameters. More... | |
Static Public Member Functions | |
| static Dyn_eos * | convert_from_Eos (const Eos &) |
Conversion operator from Eos to Dyn_eos. More... | |
| static Dyn_eos * | eos_from_file (FILE *) |
| Construction of an EOS from a binary file. More... | |
| static Dyn_eos * | eos_from_file (ifstream &) |
| Construction of an EOS from a formatted file. More... | |
Protected Member Functions | |
| Dyn_eos_poly (FILE *) | |
Constructor from a binary file (created by the function sauve(FILE*) ). More... | |
| Dyn_eos_poly (ifstream &) | |
| Constructor from a formatted file. More... | |
| void | set_auxiliary () |
Computes the auxiliary quantities gam1 , unsgam1 , gam1sgamkap from the values of gam and kap. More... | |
| virtual ostream & | operator>> (ostream &) const |
| Operator >> More... | |
| void | calcule (const Scalar &thermo, int nzet, int l_min, double(Dyn_eos::*fait)(double, const Param *) const, Param *par, Scalar &resu) const |
General computational method for Scalar 's. More... | |
Protected Attributes | |
| double | gam |
Adiabatic index  (cf. Eq. (3)) More... (cf. Eq. (3)) More... | |
| double | kap |
Pressure coefficient 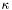 (cf. More... (cf. More... | |
| double | m_0 |
Individual particule mass 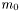 (cf. More... (cf. More... | |
| double | mu_0 |
Relativistic chemical potential at zero pressure [unit: 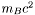 , with , with  ]. More... ]. More... | |
| double | gam1 |
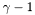 More... More... | |
| double | kapsgam1 |
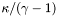 More... More... | |
| double | gamkapsgam1 |
![$(\gamma \kappa) / [(\gamma - 1)*m_0]$](form_1045.png) More... More... | |
| double | rel_mu_0 |
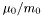 More... More... | |
| string | name |
| EOS name. More... | |
Friends | |
| Dyn_eos * | Dyn_eos::eos_from_file (FILE *) |
| The construction functions from a file. More... | |
| Dyn_eos * | Dyn_eos::eos_from_file (ifstream &) |
Detailed Description
Polytropic equation of state (relativistic case) for use in dynamical code.
This equation of state (EOS) corresponds to identical relativistic particles of rest mass is 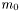 , whose total energy density e is related to their numerical density n by
, whose total energy density e is related to their numerical density n by
![\[ e(n) = {\kappa \over \gamma-1} n^\gamma + \mu_0 \, n \ , \qquad \qquad (1) \]](form_917.png)
where 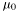 is the chemical potential at zero pressure. The relativistic (i.e. including rest mass energy) chemical potential is then
is the chemical potential at zero pressure. The relativistic (i.e. including rest mass energy) chemical potential is then
![\[ \mu(n) := {de\over dn} = {\kappa \gamma \over \gamma-1} n^{\gamma-1} + \mu_0 \ .\qquad \qquad (2) \]](form_918.png)
The pressure is given by the (zero-temperature) First Law of Thermodynamics: 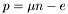 , so that
, so that
![\[ p(n) = \kappa n^\gamma \ . \qquad \qquad (3) \]](form_919.png)
The log-enthalpy is defined as the logarithm of the ratio of the enthalpy par particle by the partical rest mass energy :
![\[ H(n) := c^2 \ln \left( {e+p \over m_0 c^2\, n} \right) \ . \qquad \qquad (4) \]](form_920.png)
According to the (zero-temperature) First Law of Thermodynamics, the log-enthalpy is related to the chemical potential by
![\[ H = c^2 \ln \left( {\mu \over m_0 c^2} \right) \ . \qquad \qquad (5) \]](form_921.png)
()
Constructor & Destructor Documentation
◆ Dyn_eos_poly() [1/6]
| Lorene::Dyn_eos_poly::Dyn_eos_poly | ( | double | gamma, |
| double | kappa | ||
| ) |
Standard constructor (sets both m_0 and mu_0 to 1).
The individual particle mass 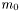 is set to the mean baryon mass
is set to the mean baryon mass  .
.
- Parameters
-
gamma adiabatic index  (cf. Eq. (3))
(cf. Eq. (3)) kappa pressure coefficient 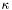
(cf. Eq. (3)) [unit: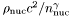 ], where
], where  and
and 
Definition at line 67 of file dyneos_poly.C.
References set_auxiliary().
◆ Dyn_eos_poly() [2/6]
| Lorene::Dyn_eos_poly::Dyn_eos_poly | ( | double | gamma, |
| double | kappa, | ||
| double | mass | ||
| ) |
Standard constructor with individual particle mass (sets mu_0 to 1).
- Parameters
-
gamma adiabatic index  (cf. Eq. (3))
(cf. Eq. (3)) kappa pressure coefficient 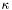 (cf. Eq. (3)) [unit:
(cf. Eq. (3)) [unit: 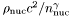 ], where
], where  and
and 
mass individual particule mass 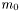 (cf. Eq. (1) [unit:
(cf. Eq. (1) [unit:  ]
]
Definition at line 76 of file dyneos_poly.C.
References set_auxiliary().
◆ Dyn_eos_poly() [3/6]
| Lorene::Dyn_eos_poly::Dyn_eos_poly | ( | double | gamma, |
| double | kappa, | ||
| double | mass, | ||
| double | mu_zero | ||
| ) |
Standard constructor with individual particle mass and zero-pressure chemical potential.
- Parameters
-
gamma adiabatic index  (cf. Eq. (3))
(cf. Eq. (3)) kappa pressure coefficient 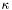 (cf. Eq. (3)) [unit:
(cf. Eq. (3)) [unit: 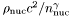 ], where
], where  and
and 
mass individual particule mass 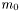 (cf. Eq. (1)) [unit:
(cf. Eq. (1)) [unit:  ]
] mu_zero Relativistic chemical potential at zero pressure [unit: 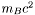 , with
, with  ]. (standard value: 1)
]. (standard value: 1)
Definition at line 85 of file dyneos_poly.C.
References set_auxiliary().
◆ Dyn_eos_poly() [4/6]
| Lorene::Dyn_eos_poly::Dyn_eos_poly | ( | const Dyn_eos_poly & | eosi | ) |
◆ Dyn_eos_poly() [5/6]
|
protected |
Constructor from a binary file (created by the function sauve(FILE*) ).
This constructor is protected because any EOS construction from a binary file must be done via the function Dyn_eos::eos_from_file(FILE*) .
Definition at line 104 of file dyneos_poly.C.
References Lorene::fread_be(), gam, kap, m_0, mu_0, and set_auxiliary().
◆ Dyn_eos_poly() [6/6]
|
protected |
Constructor from a formatted file.
This constructor is protected because any EOS construction from a formatted file must be done via the function Dyn_eos::eos_from_file(ifstream&) .
Definition at line 125 of file dyneos_poly.C.
References gam, kap, m_0, mu_0, and set_auxiliary().
◆ ~Dyn_eos_poly()
|
virtual |
Destructor.
Definition at line 146 of file dyneos_poly.C.
Member Function Documentation
◆ calcule()
|
protectedinherited |
General computational method for Scalar 's.
- Parameters
-
thermo [input] thermodynamical quantity (for instance the density field) from which the thermodynamical quantity resuis to be computed.nzet [input] number of domains where resuis to be computed.l_min [input] index of the innermost domain is which resuis to be computed [default value: 0];resuis computed only in domains whose indices are in[l_min,l_min+nzet-1] . In the other domains, it is set to zero.fait [input] pointer on the member function of class Dyn_eoswhich performs the pointwise calculation.par possible extra parameters of the EOS resu [output] result of the computation.
Definition at line 196 of file dyneos.C.
References Lorene::Scalar::get_etat().
◆ convert_from_Eos()
Conversion operator from Eos to Dyn_eos.
Works only for relativistic polytropes and tabulated EOSs.
Definition at line 120 of file dyneos.C.
References Lorene::Eos_poly::get_gam(), Lorene::Eos_poly::get_kap(), Lorene::Eos_poly::get_m_0(), Lorene::Eos_poly::get_mu_0(), Lorene::Eos::get_name(), and Lorene::Eos::identify().
◆ csound_square_nbar()
|
inherited |
Computes the sound speed squared 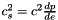 from the baryon density with extra parameters.
from the baryon density with extra parameters.
- Parameters
-
nbar [input, unit:  ] baryon density
] baryon density nzet number of domains where the derivative dln(e)/dln(H) is to be computed. l_min index of the innermost domain is which the coefficient dln(n)/dln(H) is to be computed [default value: 0]; the derivative dln(e)/dln(H) is computed only in domains whose indices are in [l_min,l_min+nzet-1] . In the other domains, it is set to zero.par possible extra parameters of the EOS
- Returns
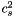 [unit: c^2]
[unit: c^2]
Definition at line 300 of file dyneos.C.
References Lorene::Dyn_eos::calcule(), Lorene::Dyn_eos::csound_square_nbar_p(), and Lorene::Tensor::get_mp().
◆ csound_square_nbar_p()
|
virtual |
Computes the sound speed squared 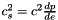 from the baryon density with extra parameters.
from the baryon density with extra parameters.
- Parameters
-
nbar [input, unit:  ] baryon density
] baryon density par possible extra parameters of the EOS
- Returns
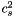 [unit: c^2]
[unit: c^2]
Implements Lorene::Dyn_eos.
Definition at line 318 of file dyneos_poly.C.
References gam, gam1, kap, kapsgam1, mu_0, and Lorene::pow().
◆ ener_nbar()
|
inherited |
Computes the total energy density from the baryon density and extra parameters.
- Parameters
-
nbar [input, unit:  ] baryon density
] baryon density nzet number of domains where the energy density is to be computed. l_min index of the innermost domain is which the energy density is to be computed [default value: 0]; the energy density is computed only in domains whose indices are in [l_min,l_min+nzet-1] . In the other domains, it is set to zero.par possible extra parameters of the EOS
- Returns
- energy density [unit:
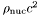 ], where
], where 
Definition at line 276 of file dyneos.C.
References Lorene::Dyn_eos::calcule(), Lorene::Dyn_eos::ener_nbar_p(), and Lorene::Tensor::get_mp().
◆ ener_nbar_p()
|
virtual |
Computes the total energy density from the baryon density and extra parameters (virtual function implemented in the derived classes).
- Parameters
-
nbar [input, unit:  ] baryon density
] baryon density par possible extra parameters of the EOS
- Returns
- energy density e [unit:
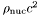 ], where
], where 
Implements Lorene::Dyn_eos.
Definition at line 298 of file dyneos_poly.C.
References gam, kapsgam1, mu_0, and Lorene::pow().
◆ ent_nbar()
|
inherited |
Computes the log-enthalpy field from the baryon density field and extra parameters.
- Parameters
-
nbar [input, unit:  ] baryon density
] baryon density nzet number of domains where the baryon density is to be computed. l_min index of the innermost domain is which the baryon density is to be computed [default value: 0]; the baryon density is computed only in domains whose indices are in [l_min,l_min+nzet-1] . In the other domains, it is set to zero.par possible extra parameters of the EOS
- Returns
- ent log-enthalpy H defined by
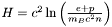 , where e is the (total) energy density, p the pressure, n the baryon density, and
, where e is the (total) energy density, p the pressure, n the baryon density, and 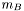 the baryon mass.
the baryon mass.
Definition at line 263 of file dyneos.C.
References Lorene::Dyn_eos::calcule(), Lorene::Dyn_eos::ent_nbar_p(), and Lorene::Tensor::get_mp().
◆ ent_nbar_p()
|
virtual |
Computes the log-enthalpy from the baryon density and extra parameters (virtual function implemented in the derived classes).
- Parameters
-
nbar [input, unit:  ] baryon density
] baryon density par possible extra parameters of the EOS
- Returns
- ent log-enthalpy H defined by
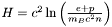 , where e is the (total) energy density, p the pressure, n the baryon density, and
, where e is the (total) energy density, p the pressure, n the baryon density, and 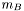 the baryon mass.
the baryon mass.
Implements Lorene::Dyn_eos.
Definition at line 288 of file dyneos_poly.C.
References gam1, gamkapsgam1, Lorene::log(), Lorene::pow(), and rel_mu_0.
◆ eos_from_file() [1/2]
|
staticinherited |
Construction of an EOS from a binary file.
The file must have been created by the function sauve(FILE*) .
Definition at line 323 of file dyneos.C.
References Lorene::fread_be().
◆ eos_from_file() [2/2]
|
staticinherited |
Construction of an EOS from a formatted file.
The fist line of the file must start by the EOS number, according to the following conventions (same as fo the classes Eos ):
- 1 = relativistic polytropic EOS (class
Dyn_eos_poly). - 2 = Newtonian polytropic EOS (class
Dyn_eos_poly_newt). - 17 = Tabulated EOS (class
Dyn_eos_tab). - 20 = Consistent EOS from table (class
Dyn_eos_cons).
The second line in the file should contain a name given by the user to the EOS. The following lines should contain the EOS parameters (one parameter per line), in the same order than in the class declaration.
◆ get_gam()
| double Lorene::Dyn_eos_poly::get_gam | ( | ) | const |
Returns the adiabatic index  (cf. Eq. (3))
(cf. Eq. (3))
Definition at line 178 of file dyneos_poly.C.
References gam.
◆ get_kap()
| double Lorene::Dyn_eos_poly::get_kap | ( | ) | const |
Returns the pressure coefficient 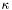 (cf.
(cf.
Eq. (3)) [unit: 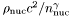 ], where
], where  and
and  .
.
Definition at line 183 of file dyneos_poly.C.
References kap.
◆ get_m_0()
| double Lorene::Dyn_eos_poly::get_m_0 | ( | ) | const |
Return the individual particule mass 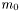 (cf.
(cf.
Eq. (1)) [unit:  ].
].
Definition at line 188 of file dyneos_poly.C.
References m_0.
◆ get_mu_0()
| double Lorene::Dyn_eos_poly::get_mu_0 | ( | ) | const |
Return the relativistic chemical potential at zero pressure [unit: 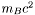 , with
, with  ].
].
Definition at line 193 of file dyneos_poly.C.
References mu_0.
◆ get_name()
|
inherited |
◆ identify()
|
virtual |
Returns a number to identify the sub-classe of Dyn_eos the object belongs to.
Implements Lorene::Dyn_eos.
◆ operator!=()
|
virtual |
Comparison operator (difference)
Implements Lorene::Dyn_eos.
Definition at line 248 of file dyneos_poly.C.
References operator==().
◆ operator=()
| void Lorene::Dyn_eos_poly::operator= | ( | const Dyn_eos_poly & | eosi | ) |
Assignment to another Dyn_eos_poly.
Definition at line 152 of file dyneos_poly.C.
References gam, kap, m_0, mu_0, Lorene::Dyn_eos::name, set_auxiliary(), and Lorene::Dyn_eos::set_name().
◆ operator==()
|
virtual |
Comparison operator (egality)
Implements Lorene::Dyn_eos.
Definition at line 204 of file dyneos_poly.C.
References gam, Lorene::Dyn_eos::identify(), identify(), kap, m_0, and mu_0.
◆ operator>>()
|
protectedvirtual |
◆ press_nbar()
|
inherited |
Computes the pressure from the baryon density and extra parameters.
- Parameters
-
nbar [input, unit:  ] baryon density
] baryon density nzet number of domains where the pressure is to be computed. l_min index of the innermost domain is which the pressure is to be computed [default value: 0]; the pressure is computed only in domains whose indices are in [l_min,l_min+nzet-1] . In the other domains, it is set to zero.par possible extra parameters of the EOS
- Returns
- pressure [unit:
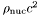 ], where
], where 
Definition at line 288 of file dyneos.C.
References Lorene::Dyn_eos::calcule(), Lorene::Tensor::get_mp(), and Lorene::Dyn_eos::press_nbar_p().
◆ press_nbar_p()
|
virtual |
Computes the pressure from the baryon density and extra parameters (virtual function implemented in the derived classes).
- Parameters
-
nbar [input, unit:  ] baryon density
] baryon density par possible extra parameters of the EOS
- Returns
- pressure p [unit:
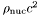 ], where
], where 
Implements Lorene::Dyn_eos.
Definition at line 308 of file dyneos_poly.C.
References gam, kap, and Lorene::pow().
◆ sauve()
|
virtual |
Save in a file.
Reimplemented from Lorene::Dyn_eos.
Definition at line 258 of file dyneos_poly.C.
References Lorene::fwrite_be(), gam, kap, m_0, mu_0, and Lorene::Dyn_eos::sauve().
◆ set_auxiliary()
|
protected |
Computes the auxiliary quantities gam1 , unsgam1 , gam1sgamkap from the values of gam and kap.
Definition at line 170 of file dyneos_poly.C.
References gam, gam1, gamkapsgam1, kap, kapsgam1, m_0, mu_0, and rel_mu_0.
◆ set_name()
|
inherited |
Friends And Related Function Documentation
◆ Dyn_eos::eos_from_file
|
friend |
The construction functions from a file.
Member Data Documentation
◆ gam
|
protected |
◆ gam1
◆ gamkapsgam1
◆ kap
|
protected |
◆ kapsgam1
◆ m_0
|
protected |
◆ mu_0
|
protected |
◆ name
◆ rel_mu_0
The documentation for this class was generated from the following files:
