A binary black hole system is constructed on a Cartesian grid from data stored in a file resulting from a computation by Grandclement, Gourgoulhon and Bonazzola, Phys. Rev. D 65, 044021 (2002).
All the quantities are in units derived from the length
scale defined by the coordinate radius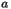 
of black hole 1 apparent horizon
(throat).
Importation of Lorene data is performed by means of the constructor
Bin_BH::Bin_BH(int, const double*, const double*, const double*, const char*).
This constructor takes general arrays for the location of the Cartesian coordinates
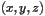, i.e. it does not assume that the grid is a uniform one. Note also
that these arrays are 1-D, as well as all the metric fields,
in order to be use with any ordering of the 3-D storage.
This class is very simple, with all data members being public. A typical example of use is the following one
* // Define the Cartesian grid by means of the arrays xg, yg, zg:
* for (int i=0; i<nb_points; i++) {
* xg[i] = ...
* yg[i] = ...
* zg[i] = ...
* }
*
* // Read the file containing the spectral data and evaluate
* // all the fields on the Cartesian grid :
*
* Bin_BH binary_system(nb_points, xg, yg, zg, fill, datafile) ;
*
* // Extract what you need :
*
* double* gamma_xx = binary_system.g_xx ; // metric coefficient g_xx
*
* double* shift_x = binary_system.beta_x ; // x comp. of shift vector
*
* ...
*
* // Save everything in an ASCII file :
*
* ofstream file_ini("ini.d") ;
* binary_system.save_form(file_ini) ;
* file_ini.close() ;
*
*
![[more]](icon1.gif)
double omega
]
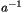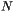at the np grid points (1-D array)
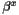of the shift vector of corotating coordinates [unit: 
]
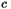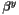of the shift vector of corotating coordinates [unit: 
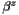of the shift vector of corotating coordinates [unit: 
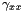at the grid points (1-D array)
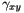at the grid points (1-D array)
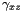at the grid points (1-D array)
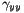at the grid points (1-D array)
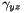at the grid points (1-D array)
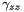at the grid points (1-D array)
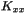of the extrinsic curvature at the grid points (1-D array) [unit: 
]
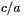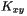of the extrinsic curvature at the grid points (1-D array) [unit: 
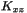of the extrinsic curvature at the grid points (1-D array) [unit: 
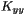of the extrinsic curvature at the grid points (1-D array) [unit: 
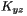of the extrinsic curvature at the grid points (1-D array) [unit: 
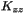of the extrinsic curvature at the grid points (1-D array) [unit: 
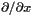of the conformal factor 
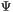[unit: 
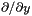of the conformal factor 
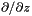of the conformal factor 
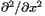of the conformal factor 
]
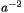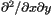of the conformal factor 
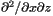of the conformal factor 
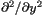of the conformal factor 
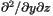of the conformal factor 
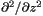of the conformal factor 
double omega